Combien coûte x par x?

Multiplier x par x vous obtenez x².

X² se lit comme "X carré" ou simplement "X carré".

Pourquoi x par x est x²?

Le résultat de x par x est X².

C'est un résultat très facile à vérifier, grâce au Propriété de la multiplication des pouvoirs de base égale.

En algèbre, la lettre X est utilisée comme moyen d'appeler un montant qui prend des valeurs inconnues, bien que d'autres lettres puissent également être utilisées.

La propriété de la multiplication des pouvoirs de la même base stipule que "Lors de la multiplication de deux bases identiques, la même base est écrite et les exposants sont ajoutés".

X^pour∙ x^b = x^{A + B}

L'exposant égal à 1 du X est généralement omis, de sorte que X¹ = x.

Si nous voulons savoir combien x par x:

La la base est x (la même chose est écrite) et Des exposants sont ajoutés à + b (Ses valeurs sont égales à 1):

x ∙ x = x^{1 + 1} = x²

Exemples de la propriété de la multiplication des pouvoirs de base égale

Regardons quelques exemples numériques très simples:

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16

(−2) × (−2) = 2² = 4

Notez que le signe négatif ci-dessus ne modifie pas le résultat, car selon la loi des signes, la multiplication de deux quantités négatives est obtenue un résultat positif.

Dans les exemples précédents, des nombres entiers ont été utilisés, mais l'opération est également valable pour les nombres décimaux, fractionnaux, réels et complexes.

La zone d'un carré

Le carré d'un nombre apparaît fréquemment dans le calcul des zones des chiffres géométriques réguliers. Par exemple, celui du carré, qui est un seul polygone à quatre faces, qui ont tous la même mesure.

Peut vous servir: système d'équations: méthodes de solution, exemples, exercices

La zone d'un carré est donnée par le carré de son côté, si elle est appelée «x», alors la zone a du carré vaut x².

Exemple de la zone d'un carré

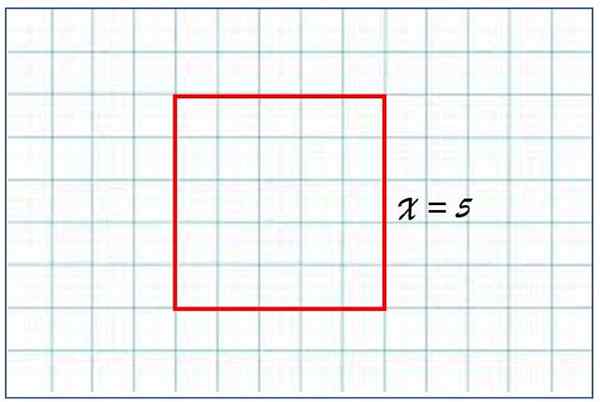
La zone carrée A dont le côté est x = 5 unités est égal à:

A = 5² = 5 × 5 = 25 unités de surface

Un carré sur le côté égal à 5 ​​unités arbitraires de longueur a une superficie de 25 unités de superficie. Source: F. Zapata.

Ce résultat a du sens, car le carré se compose de 5 lignes et 5 colonnes de plus petits carrés, du côté égal à 1. Si le lecteur observe attentivement la figure, il se rendra compte que la place rouge se compose de 25 petits carrés de zone unitaire.

Important:

Les unités de cet exemple sont arbitraires, elles peuvent être des mètres, des centimètres, des pouces ou. Ici, ils n'ont pas été spécifiés, mais en tout cas, la zone respective serait donnée en mètres au carré, au carré, à des pouces carrés ou à. La zone est toujours donnée en unités de longueur carrée.

Le carré des nombres fractionnaires et décimaux

Pour trouver le carré d'un nombre fractionnaire, qui est composé d'un numéro et d'un dénominateur, séparés par la ligne de fraction, il est nécessaire de multiplier le numérateur avec lui-même, ainsi que le dénominateur, obtenant un nouveau nombre fractionnaire.

Exemples de nombres carrés carrés

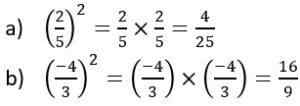
Exemples de nombres carrés

Quant au carré d'un nombre décimal, nous devons suivre les règles de multiplication pour les nombres décimaux.

a) 0.6² = 0.6 × 0.6 = 0.36

b) (−0.4)² = (−0.4) × (−0.4) = 0.16

À la fois dans cet exemple et dans l'une des sections précédentes correspondantes, il est observé que le carré d'un nombre négatif est toujours positif. Cela est vrai pour les pouvoirs égaux, pas seulement pour le carré.

Peut vous servir: ensembles équivalents: quelles sont, explication, exemples