Combien de solutions une équation quadratique a-t-elle?

Une équation quadratique ou une équation au deuxième degré ne peut avoir zéro, une ou deux solutions réelles, selon les coefficients qui apparaissent dans ladite équation. Si vous travaillez sur des nombres complexes, vous pouvez dire que chaque équation quadratique a deux solutions.

Pour démarrer une équation quadratique, c'est une équation de la forme ax² + bx + c = 0, où a, b et c sont des nombres réels et x est une variable.

On dit que x1 est une solution de l'équation quadratique précédente si lors du remplacement de x par x1, l'équation est satisfaite, c'est-à-dire si a (x1) ² + b (x1) + c = 0.

Si vous avez par exemple l'équation x²-4x + 4 = 0, alors x1 = 2 est la solution, puisque (2) ² (2) +4 = 4-8 + 4 = 0.

Au contraire, si x2 = 0 est remplacé, il est obtenu (0) ²-4 (0) +4 = 4 et comme 4 ≠ 0 alors x2 = 0 n'est pas une solution de l'équation quadratique.

Solutions d'une équation quadratique

Le nombre de solutions d'une équation quadratique peut être séparé dans deux cas qui sont:

1.- En nombre réel

Lorsque vous travaillez avec des nombres réels, les équations quadratiques peuvent avoir:

-Solutions zéro: c'est-à-dire qu'il n'y a pas de nombre réel qui satisfait l'équation quadratique. Par exemple, l'équation donnée x² + 1 = 0, il n'y a pas de nombre réel tel qui satisfait ladite équation, car les deux x² sont supérieurs ou égaux à zéro et 1 est plus strict que zéro, de sorte que sa somme sera plus élevée Strict que zéro.

-Une solution répétée: Il y a une seule valeur réelle qui satisfait l'équation quadratique. Par exemple, la seule solution de l'équation x²-4x + 4 = 0 est x1 = 2.

-Deux solutions différentes: Il y a deux valeurs qui satisfont l'équation quadratique. Par exemple, x² + x-2 = 0 a deux solutions différentes qui sont x1 = 1 et x2 = -2.

2.- En nombres complexes

Lorsque vous travaillez avec des nombres complexes, les équations quadratiques ont toujours deux solutions qui sont Z1 et Z2 où Z2 est le conjugué de Z1. De plus, ils peuvent être classés comme:

-Complexes: Les solutions sont de la forme z = p ± qi, où p et q sont des nombres réels. Ce cas correspond au premier cas de la liste précédente.

-Complexes purs: C'est lorsque la partie réelle de la solution est égale à zéro, c'est-à-dire que la solution a la forme z = ± qi, où q est un nombre réel. Ce cas correspond au premier cas de la liste précédente.

-Complexes avec une partie imaginaire égale à zéro: C'est lorsque la partie complexe de la solution est égale à zéro, c'est-à-dire que la solution est un nombre réel. Ce cas correspond aux deux derniers cas de la liste précédente.

Comment les solutions d'une équation quadratique sont-elles calculées?

Pour calculer les solutions d'une équation quadratique, une formule connue sous le nom de «résolution» est utilisée, qui dit que les solutions d'une équation AX² + BX + C = 0 sont données par l'expression de l'image suivante:

La quantité qui apparaît dans la racine carrée est appelée discriminante de l'équation quadratique et est notée par la lettre "D".

L'équation quadratique aura:

-Deux vraies solutions oui, et seulement oui, d> 0.

-Une vraie solution répétée si, et seulement si, d = 0.

-Zéro solutions réelles (ou deux solutions complexes) oui, et seulement oui, D<0.

Exemples

-Les solutions de l'équation x² + x-2 = 0 sont données par:

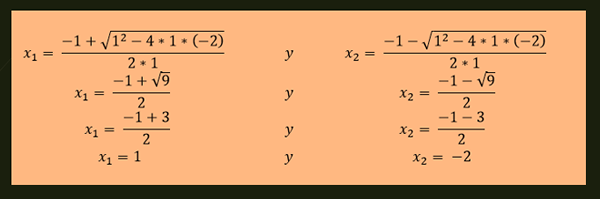
-L'équation x²-4x + 4 = 0 a une solution répétée qui est donnée par:

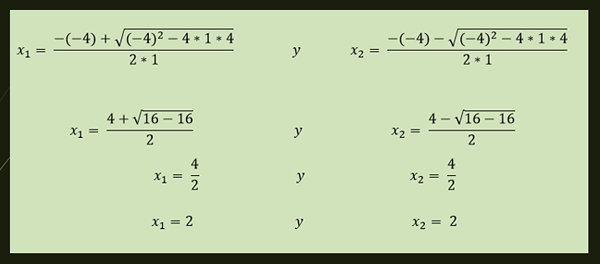
-Les solutions de l'équation X² + 1 = 0 sont données par:

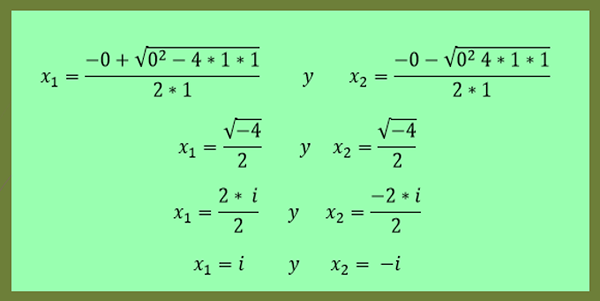
Comme on peut le voir dans ce dernier exemple, x2 est le conjugué de x1.