Longueur de corde (géométrie), théorème et exercices

Ongle corde, En géométrie plate, c'est le segment de ligne qui rejoint deux points d'une courbe. On dit que la ligne contenant ce segment est une ligne de séchage à la courbe. C'est souvent une circonférence, mais vous pouvez certainement dessiner des cordes dans de nombreuses autres courbes, comme les ellipses et les paraboles.

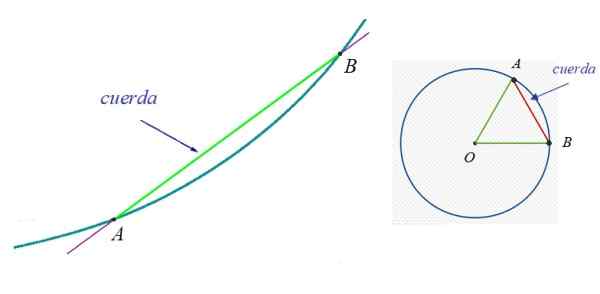
Dans la figure 1 à gauche, il y a une courbe, à quels points A et B appartiennent. La corde entre A et B est le segment vert. À droite est une circonférence et une de leurs cordes, car il est possible de tracer l'infini.

Figure 1. À gauche, la corde d'une courbe arbitraire et à droite la corde d'un cercle. Source: Wikimedia Commons.

Dans la circonférence, son diamètre est particulièrement intéressant, qui est également connu sous le nom Corde majeure. C'est une corde qui contient toujours le centre de la circonférence et mesure deux fois le rayon.

La figure suivante est représentée par le rayon, le diamètre, une corde et aussi l'arc d'un cercle. Identifier correctement chacun est important lors de la résolution de problèmes.

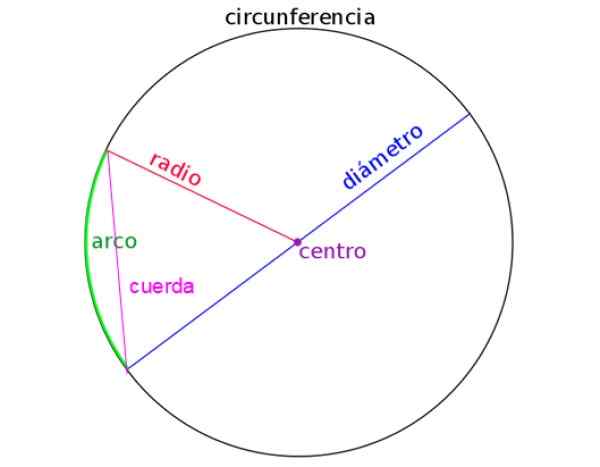Figure 2. Éléments de la circonférence. Source: Wikimedia Commons.

[TOC]

Longueur de corde d'une circonférence

Nous pouvons calculer la longueur de la corde dans un cercle à partir des figures 3A et 3B. Notez qu'un triangle est toujours formé avec deux côtés égaux (isocèles): les segments OA et OB, qui mesurent R, le rayon de la circonférence. Le troisième côté du triangle est le segment AB, appelé C, qui est précisément la longueur de la corde.

Il est nécessaire de tracer une ligne perpendiculaire à la corde C pour bissection à l'angle θ qui existe entre les deux radios et dont le sommet est le centre ou la circonférence. C'est un angle central -Parce que son sommet est le centre et la ligne bissectrice est également sécable de la circonférence.

Il peut vous servir: propriétés radicales

Immédiatement deux rectangles se forment, dont l'hypoténuse. Depuis la bissectrice, et avec elle le diamètre, se divise en deux parties égales à la corde, il s'avère que l'une des jambes est la moitié de C, comme indiqué sur la figure 3B.

De la définition du sein d'un angle:

sin (θ / 2) = opposé / hypotenusa cateto = (c / 2) / r

Donc:

sin (θ / 2) = c / 2r

C = 2r sen (θ / 2)

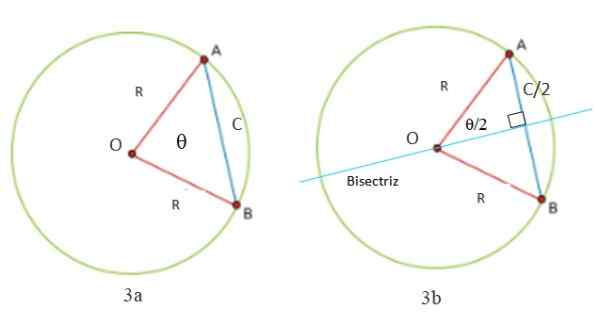figure 3. Le triangle formé par deux radios et une corde de circonférence est isocèle (figure 3), car il a deux côtés égaux. La bissectrice le divise en deux triangles de rectangles (figure 3B). Source: Préparé par F. Zapata.

Théorème de cordes 

Le théorème des cordes dit:

Si deux cordes se croisent à un moment donné, le produit de la longueur des segments qui apparaissent sur l'une des chaînes, est égal au produit des longueurs des segments définis dans l'autre corde.

La figure suivante montre deux chaînes de la même circonférence: AB et CD, qui se croisent au point P. Dans la corde AB, les segments AP et PB sont définis, tandis que CP et PD sont définis dans la corde de CD. Ensuite, selon le théorème:

AP . PB = CP . P.S

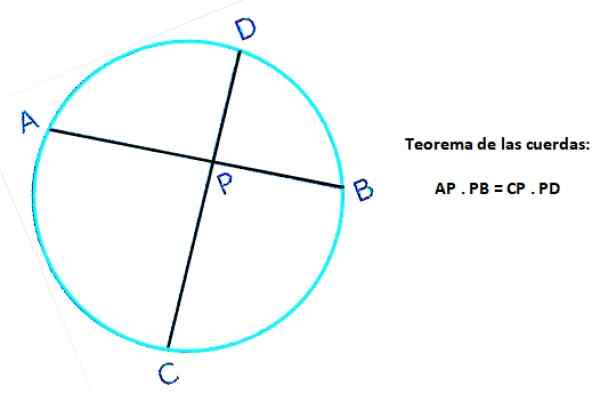Figure 4. Le théorème de la corde d'une circonférence. Source: F. Zapata.

Exercices de cordes résolues

- Exercice 1

Un cercle a une corde de 48 cm, à 7 cm du centre. Calculez la zone du cercle et le périmètre de la circonférence.

Solution  

Pour calculer le cercle dans une zone, il suffit de connaître le rayon de la circonférence au carré, car il est rempli:

A = π.R²

Maintenant, la figure formée avec les données fournies est un triangle rectangle, dont les jambes sont respectivement de 7 et 24 cm.

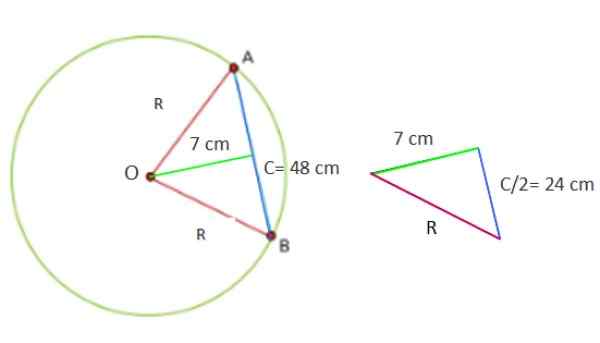Figure 5. Géométrie pour l'exercice résolu 1. Source: F. Zapata.

Donc pour trouver la valeur de r² Le théorème Pythagore C est appliqué directement² = A² + b², Puisque r est l'hypoténuse du triangle:

Peut vous servir: angle nul: définition et caractéristiques, exemples, exercices

R² = (7 cm)² + (24 cm)² = 625 cm²

Ensuite, la zone demandée est:

A = π. 625 cm² = 1963.5 cm²

Quant au périmètre ou à la longueur L de la circonférence, il est calculé par:

L = 2π. R

Remplacement des valeurs:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Exercice 2

Déterminez la longueur de la corde d'un cercle dont l'équation est:

X² + et² - 6x - 14y -111 = 0

Il est connu que les coordonnées du point médian de la corde sont P (17/2; 7/2).

Solution

Le point médian de la corde P n'appartient pas à la circonférence, mais les points extrêmes de la corde oui. Le problème peut être résolu au moyen du théorème des cordes précédemment énoncé, mais d'abord il est pratique.

Étape 1: Obtenez l'équation canonique de la circonférence

L'équation canonique de la circonférence avec le centre (H, K) est:

(X-H)² + (et K)² = R²

Pour l'obtenir, il est nécessaire de compléter les carrés:

(X² - 6x) + (et² - 14y) -111 = 0

Notez que 6x = 2.(3x) et 14y = 2.(7y), de sorte que l'expression précédente est réécrite ainsi, inchangée:

(X² - 6x + 3²-3²) + (et² - 14y + 7²-7²) -111 = 0

Et maintenant, se souvenant de la définition du produit notable (A-B)² = A² - 2AB + B² Il peut être écrit:

(X - 3)² - 3² + (et - 7)² - 7² - 111 = 0

= (x - 3)² + (et - 7)² = 111 + 3² + 7² → (x - 3)² + (et - 7)² = 169

La circonférence a un centre (3,7) et une radio r = √169 = 13. La figure suivante montre le graphique de la circonférence et les chaînes qui seront utilisées dans le théorème:

Peut vous servir: quels sont les 7 éléments de la circonférence?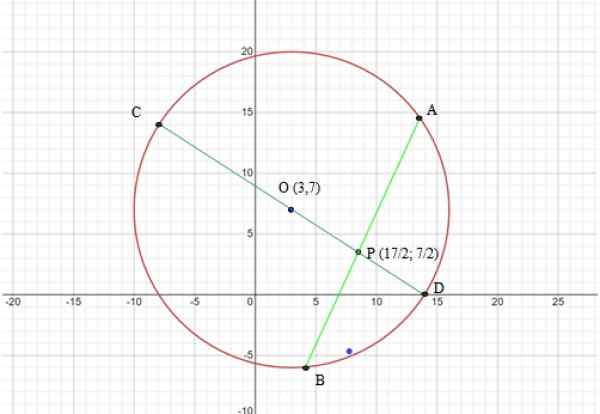Figure 6. Graphique de la circonférence de l'exercice résolu 2. Source: F. Zapata via la calculatrice graphique en ligne Mathway.

Étape 2: Déterminez les segments à utiliser dans le théorème des chaînes

Les segments à utiliser sont les chaînes CD et AB, selon la figure 6, les deux sont coupées au point P, par conséquent:

CP . Pd = ap. PB

Maintenant, nous allons trouver la distance entre les points O et P, car cela nous donnera la longueur du segment OP. Si nous ajoutons le rayon à cette longueur, nous aurons le segment CP.

La distance d_{Faire un coup de pouce} Entre deux points de coordonnées (x₁,et₁) et (x₂,et₂) est:

d_{Faire un coup de pouce}² = OP² = (x₂ - X₁)² + (et₂ - et₁)² = (3- 17/2)² + (7-7 / 2)² = 121/4 + 49/4 = 170/4

d_{Faire un coup de pouce} = Op = √170 / 2

Avec tous les résultats obtenus, plus le graphique, nous construisons la liste suivante des segments (voir figure 6):

CO = 13 cm = R

OP = √170 / 2 cm

Cp = op + r = 13 + √170 / 2 cm

Pd = od - op = 13 - √170 / 2 cm

Ap = pb

2.AP = longueur de corde

Remplacement dans le théorème des chaînes:

CP . Pd = ap . Pb = [(13 + √170 / 2) . (13 -√170 / 2)] = AP²

[169-170 / 4] = AP²

253/2 = AP²

Ap = √ (253/2)

La longueur de la corde est 2.Ap = 2 (√253 / 2) = √506

Le lecteur pourrait-il résoudre le problème d'une autre manière?

Les références

1. Baldor, un. 2004. Géométrie plate et espace avec trigonométrie. Publications culturelles s.POUR. de c.V. Mexique.
2. C-K12. Lenght d'un accord. Récupéré de: CK12.org.
3. Escobar, J. La circonférence. Récupéré de: mathématiques.toi.Édu.co.
4. Villena, m. Conique. Récupéré de: dspace.Époustoufler.Édu.CE.
5. Wikipédia. Corde (géométrie). Récupéré de: est.Wikipédia.org.