Description du théorème de Norton, applications, exemples et exercices

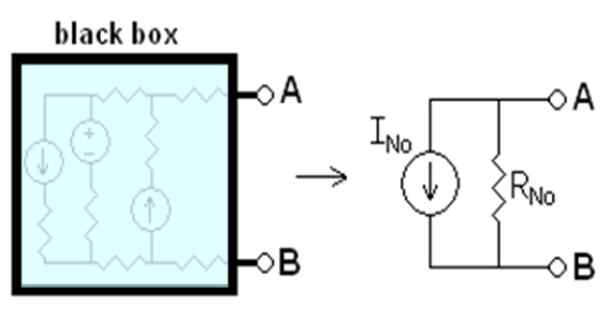
Il Théorème de Norton, qui s'applique aux circuits électriques, établit qu'un circuit linéaire avec deux bornes A et B, peut être remplacé par un autre complètement équivalent, composé d'une source de courant appelée I_Non connecté en parallèle avec une résistance r_Non.

Dit actuel je_Non J'ai entendu_N C'est celui qui coulerait entre les points A et B, s'ils étaient courts-circuits. La résistance r_N C'est la résistance équivalente entre les terminaux, lorsque toutes les sources indépendantes sont désactivées. Tout dit est schématique dans la figure 1.

Figure 1. Circuit équivalent de Norton. Source: Wikimedia Commons. Drumkid [cc by-sa 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

La boîte noire de la figure contient le circuit linéaire qui sera remplacé par son équivalent Norton. Un circuit linéaire est celui dans lequel l'entrée et la sortie ont une dépendance linéaire, comme la relation entre la tension V et le courant direct I dans un élément ohmique: v = i.R.

Cette expression correspond à la loi d'Ohm, où R est une résistance, qui peut également être une impédance, s'il s'agit d'un circuit de courant alternatif.

Le théorème de Norton a été développé par l'électriciste et inventeur Edward L ingénieur. Norton (1898-1983), qui a travaillé longtemps pour Bell Laboratories.

[TOC]

Applications du théorème de Norton

Quand ils ont des réseaux très compliqués, avec de nombreuses résistances ou impédances et vous voulez un circuit plus petit et plus gérable.

De cette façon, le théorème de Norton est très important lors de la conception de circuits avec plusieurs éléments, ainsi que d'étudier leur réponse.

Relation entre les théorèmes de Norton et Thevenin

Le théorème de Norton est le théorème du double Thevenin, ce qui signifie qu'ils sont équivalents. Le théorème de Thevenin indique que la boîte noire de la figure 1 peut être remplacée par une source de tension de série par une résistance, appelée résistance à Thevenin R_E. Ceci est exprimé dans la figure suivante:

Peut vous servir: Mécanique des matériaux: histoire, domaine d'étude, applications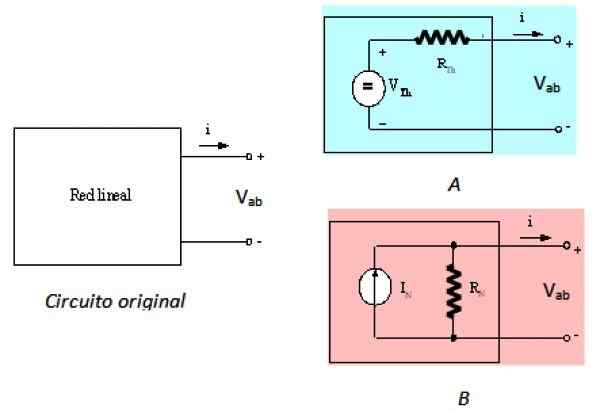 Figure 2. Circuit gauche d'origine, et ses équivalents de Thévenin et Norton. Source: F. Zapata.

Le circuit de gauche est le circuit d'origine, le réseau linéaire dans la boîte noire, le circuit jusqu'à la droite est l'équivalent de Thevenin et du circuit B C'est l'équivalent de Norton, comme décrit. Vu à partir des bornes A et B, les trois circuits sont équivalents.

Observez maintenant cela:

-Dans le circuit d'origine, la tension entre les bornes est V_{UN B}.

-V_{UN B}  = V_E dans le circuit POUR

-Enfin, V_{UN B}  = I_N.R_N dans le circuit B

Si les bornes A et B sont court-circuits dans les trois circuits, il doit être rempli que la tension et le courant entre ces points doivent être les mêmes pour les trois, car ils sont équivalents. Ensuite:

-Dans le circuit d'origine, le courant est i.

-Pour le circuit A, le courant est i = V_E / R_E, Selon la loi d'Ohm.

-Enfin dans le circuit B, le courant est i_N

Par conséquent, il est conclu que les résistances de Norton et de Thevenin ont la même valeur, et que le courant est donné par:

i = i_N = V_E / R_E = V_E / R_N

Exemple

Pour appliquer correctement le théorème de Norton, les étapes suivantes sont suivies:

-La section de circuit pour laquelle l'équivalent de Norton sera trouvé à partir du réseau est isolée du réseau.

-Dans le circuit restant, indiquez les bornes A et B.

-Remplacez les sources de tension par des circuits courts et des courants par des circuits ouverts, pour trouver la résistance équivalente entre les bornes A et B. C'est r_N.

-Renvoyez toutes les sources à leurs positions d'origine, court-circuit les bornes A et B et trouver le courant qui circule entre eux. C'est moi_N.

Peut vous servir: Effet Doppler: description, formules, cas, exemples

-Dessinez le circuit équivalent de Norton en fonction de ce qui est indiqué sur la figure 1. La source actuelle et la résistance équivalente sont en parallèle.

Vous pouvez également appliquer le théorème de Thevenin pour trouver R_E, que nous savons déjà est égal à r_N, Ensuite, par la loi d'Ohm, vous pouvez trouver je_N Et le circuit résultant est dessiné.

Et maintenant, regardons un exemple:

Trouvez l'équivalent de Norton entre les points A et B du circuit suivant:

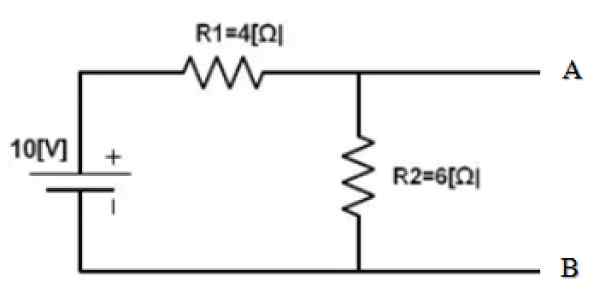figure 3. Exemple de circuit. Source: F. Zapata.

La partie du circuit est déjà isolée dont l'équivalent doit être trouvé. Et les points A et B sont clairement déterminés. Ce qui suit est de court-circuit la source de 10 V et de trouver la résistance équivalente du circuit obtenu:

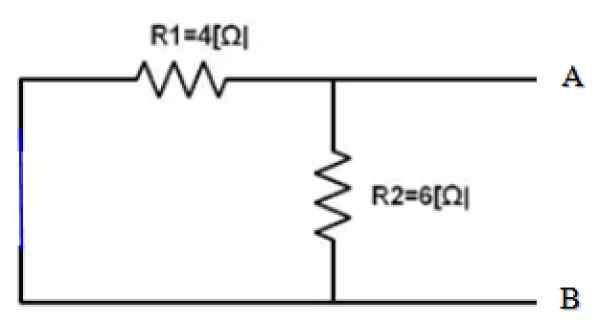Figure 4. Source court-circuit. Source: F. Zapata.

Vues à partir des bornes A et B, les deux résistances R₁ et r₂ Ils sont donc en parallèle:

1 / r_égaliseur = 1 / r₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_égaliseur = 12/5 Ω = 2.4 Ω

Ensuite, la source est renvoyée à sa place et les points A et B sont des circuits courts pour trouver le courant qui y circule, ce sera_N. Dans ce cas:

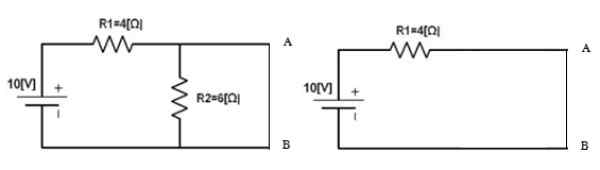Figure 5. Circuit pour calculer le courant de norton. Source: F. Zapata.

Toi_N = 10 v / 4 Ω = 2.5 a

Norton équivalent

Enfin, l'équivalent de Norton avec les valeurs trouvées est dessinée:

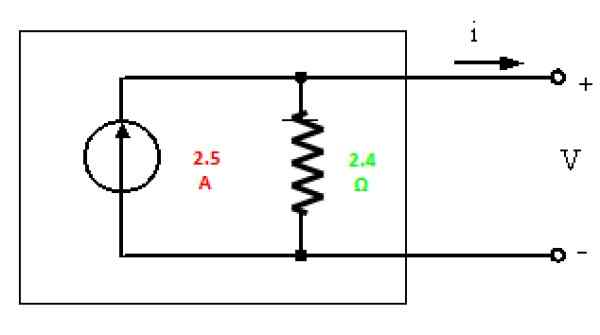Figure 6. Norton équivalent du circuit de la figure 3. Source: F. Zapata.

Exercice résolu

Dans le circuit de la figure suivante:

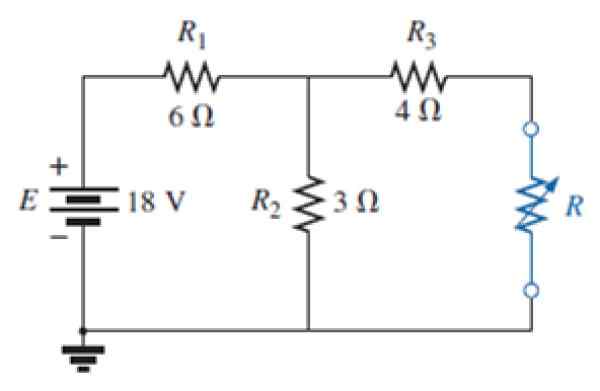Figure 7. Circuit pour l'exercice résolu. Source: Alexander, C. 2006. Fondations du circuit électrique. 3e. Édition. Mc Graw Hill.

a) Trouver le circuit équivalent de Norton du réseau de résistance au bleu extérieur.

b) Trouver également l'équivalent de Thévenin.

Solution à

Suivant les étapes indiquées ci-dessus, la source doit être court-circuit:

Peut vous servir: diffraction du son: ce qui consiste en exemples, applications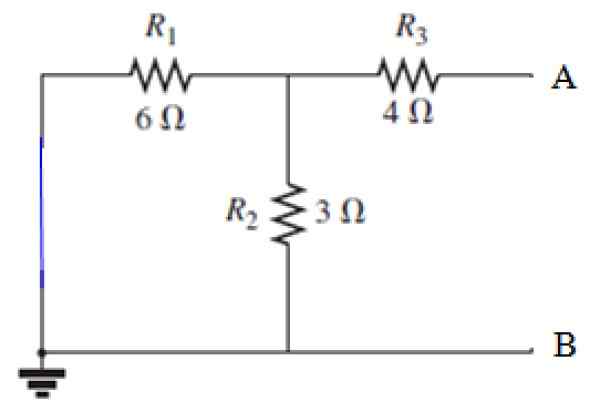 Figure 8. Source du circuit court dans le circuit de la figure 7. Source: F. Zapata.

Calcul RN

Vue à partir des bornes A et B, résistance R₃ est en série avec le parallèle formé par les résistances R₁ et r₂, Calculons d'abord la résistance équivalente de ce parallèle:

1 / r₁₂ = (1/6) + (1/3) Ω^-1 = 1/2 Ω^-1  → R_égaliseur = 2/1 Ω = 2Ω

Et puis ce parallèle est en série avec r_3, de sorte que la résistance équivalente est:

R_égaliseur = 2 Ω + 4 Ω = 6 Ω

C'est la valeur des deux r_N Depuis R_E, Comme expliqué précédemment.

Calcul de

Ensuite, les terminaux A et B sont des circuits courts, renvoyant la source à sa place:

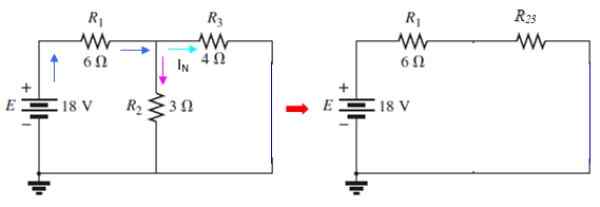Figure 9. Circuits de courant Norton. Source: F. Zapata.

Le courant passant par i₃ est le actuel i_N recherché, qui peut être déterminé avec la méthode de maillage ou en utilisant des séries et parallèles. Dans ce circuit r₂ et r₃ Ils sont en parallèle:

1 / r₂₃ = (1/3) + (1/4) ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

La résistance r₁ Il est en série avec ce parallèle, alors:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Le courant qui sort de la source (couleur bleue) est calculé par la loi d'Ohm:

V = i. R → i = v / r = 18 v / (54/7 Ω) = 7/3 A

Ce courant est divisé en deux parties: une qui traverse R₂ Et un autre qui traverse r₃. Cependant, le courant qui traverse le r parallèle₂₃ C'est la même chose qui passe par r₁, comme on peut le voir dans le circuit intermédiaire de la figure. La tension là-bas est:

V₂₃ = I.R₂₃ = (7/3) A .(12/7) ω = 4 V

Les deux résistances r₂ et r₃ Ils sont à cette tension, car ils sont donc en parallèle:

Toi₃ = V₂₃ / R₃ = 4 v / 4 Ω = 1 a

Nous avons déjà le courant Norton recherché, car comme indiqué précédemment, je₃ = I_N, ensuite:

Toi_N = 1 a

Norton équivalent

Tout est prêt à dessiner l'équivalent de Norton de ce circuit entre les points A et B:

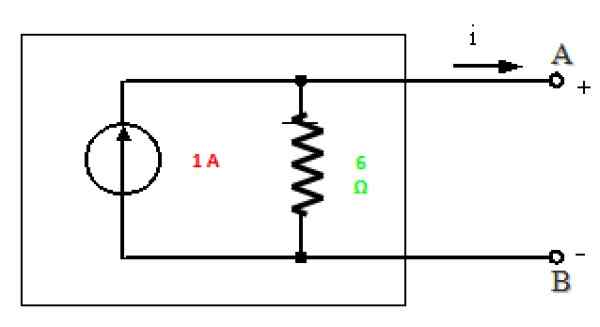Figure 10. NORTON Équivalent du circuit de la figure 7. Source: F. Zapata.

Solution B

Trouver l'équivalent de Thévenin est très simple, car R_E = R_N= 6 Ω et comme expliqué dans les sections précédentes:

V_E = I_N. R_N = 1 a . 6 Ω = 6 V

Le circuit équivalent de Thévenin est:

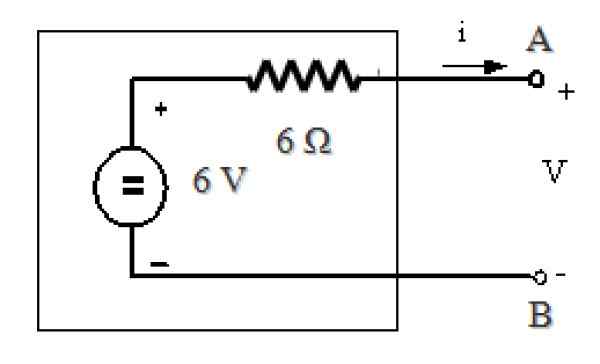Figure 11. L'équivalent de Thevenin du circuit de la figure 7. Source: F. Zapata.

Les références

1. Alexander, C. 2006. Fondations du circuit électrique. 3e. Édition. Mc Graw Hill.
2. Boylestad, R. 2011. Introduction à l'analyse des circuits. 2e. Édition. Pearson.
3. Dorf, R. 2006. Introduction aux circules électriques. 7e. Édition. John Wiley & Sons.
4. Edminister, J. mille neuf cent quatre vingt seize. Circuits électriques. Série Schaum. 3e. Édition. Mc Graw Hill.
5. Wikipédia. Théorème de Norton . Récupéré de: c'est.Wikipédia.org.