Coefficient de Poisson Coefficient, formules, valeurs, exemples

Il Coefficient de Poisson C'est une quantité sans dimension, caractéristique de chaque matériau. C'est un indicatif de la déformation d'un morceau de matériau avant l'application de certains efforts.

Lorsqu'une pièce de matériau qui subit une tension ou une compression subit une déformation, le quotient entre la déformation transversale et la déformation longitudinale est précisément le coefficient de Poisson.

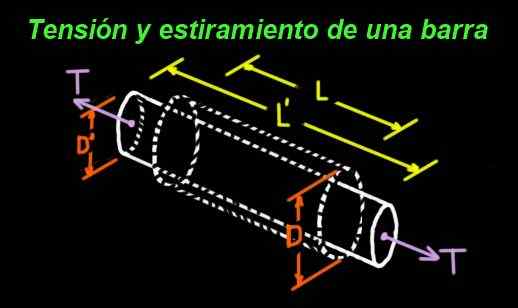
Figure 1. Le coefficient de Poisson mesure la relation entre l'étirement longitudinal et le rétrécissement transversal. (Préparé par Ricardo Pérez)

Par exemple, un cylindre en caoutchouc qui subit une tension à ses extrémités est étiré dans le sens longitudinal, mais il est transversalement étroit. La figure 1 montre une barre dont les dimensions originales sont: Long L et Diamètre D.

La barre est soumise à une tension t par ses extrémités, et en conséquence de cette tension souffre d'un étirement, de sorte que la nouvelle longueur est l '> l. Mais lors de l'étirement, un rétrécissement de son diamètre se produit également à la nouvelle valeur: D ' < D.

Le quotient entre l'étirement (positif) et le rétrécissement (négatif) multiplié par (-1), est un nombre positif entre 0 et 0,5. Ce nombre est le coefficient de Poisson So-appelé ν (lettre grecque).

[TOC]

Formule de coefficient de Poisson

Pour calculer le coefficient de Poisson, il est nécessaire de déterminer la déformation unitaire longitudinale et transversale.

Déformation de l'unité longitudinale ε_L C'est le tronçon divisé entre la longueur d'origine:

ε_L = (L '- l) / l

De même, une déformation unitaire transversale ε_T C'est le rétrécissement radial divisé entre le diamètre d'origine:

ε_T = (D '- d) / d

Par conséquent, le coefficient de Poisson est calculé par la formule suivante:

ν = - ε_T / ε_L 

Relation avec le module d'élasticité et le module de rigidité

Le coefficient de Poisson ν est lié au module ET d'élasticité (ou de jeune module) et avec le module de rigidité g, par la formule suivante:

Peut vous servir: optique géométrique: quelles études, lois, applications, exercices

ν = e / (2g) - 1

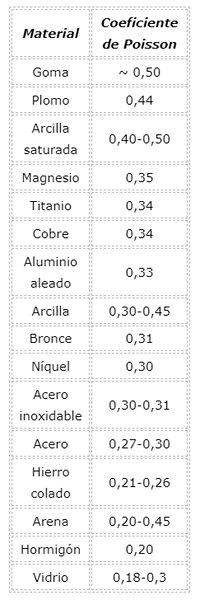
Valeur du coefficient de Poisson pour les matériaux

Figure 2. L'acier inoxydable a un coefficient de Poisson entre 0,30 et 0,31. Source: Pixabay.

Exemples de calcul

Exemple 1

Une barre d'un certain matériau plastique a une longueur de 150 mm et une section circulaire de 20 mm de diamètre. Lorsqu'une force de compression de 612,25 kg-F est soumise à une force de compression, un raccourcissement de 14 mm est observé et simultanément une augmentation de 0,85 mm de diamètre de la barre.

Calculer:

a) Déformation unitaire longitudinale.

b) déformation unitaire transversale.

c) Coefficient de Poisson de ce matériel.

d) Le module d'élasticité du jeune correspondant au matériau.

e) le module de rigidité pour ce plastique.

Solution à

Rappelons que la déformation longitudinale de l'unité εl est l'étirement divisé par la longueur d'origine:

εl = (l '- l) / l

εl = (-14 mm) / 150 mm = -0,0933

Notez que la déformation unitaire longitudinale est sans dimension et, dans ce cas, elle a donné des négatifs car il y a eu une diminution de sa dimension longitudinale.

Solution B

De même, la déformation transversale unitaire εt est un rétrécissement radial, divisé par le diamètre d'origine:

εt = (d '- d) / d

εt = (+0,85 mm) / 20 mm = 0,0425

La déformation unitaire transversale a été positive car il y a eu une augmentation du diamètre de la barre.

Solution C

Pour le calcul du coefficient de Poisson, nous devons nous rappeler qu'il est défini comme le négatif du quotient entre la déformation transversale et la déformation longitudinale:

ν = - εt / εl 

ν = - 0,0425 / (-0,0933) = 0,4554

Il faut se rappeler que le coefficient de Poisson est un nombre positif sans dimension et pour la plupart des matériaux, il se situe entre 0 et 0,5.

Peut vous servir: loi Darcy

Solution d

Le module d'élasticité de Young, désigné par la lettre E, est la constante de proportionnalité dans la loi de Hooke. Grâce à E, l'effort normal σl est lié à la déformation unitaire εl, comme suit:

σl = e εl 

L'effort normal est défini comme le quotient entre la force normale (dans ce cas parallèle à l'axe de la barre) et la section transversale:

σl = f / a = f / (π / 4 * d ^ 2)

Dans cet exercice, la force F est de 612,25 kg-F, qui sera faite aux Newtons qui est l'unité de force:

F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kN

Pour sa part, la section transversale A est:

A = (π / 4 * d ^ 2) = (3 1416/4) * (20 * 10 ^ -3 m) ^ 2 = 3 1416 * 10 ^ -4 m ^ 2

Enfin, l'effort normal appliqué à la barre est:

σl = f / a = 6000 n / 3 1416 * 10 ^ -4 m ^ 2 = 19.098.593 PA = 19 098 MPA

Pour calculer le module d'élasticité du Young, nous effacons et de la loi de Hooke σl = E εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPa

Solution E

Le module de rigidité R est lié au module EG de Young et au coefficient de Poisson ν par cette formule:

E / (2 g) = 1 + ν 

De là, vous pouvez effacer G:

G = e / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa

Exemple 2

Vous avez un câble de 4 mm et 1 m de diamètre. Sachant que le module Copper Young est de 110000 MPa et que son coefficient de Poisson est de 0,34, il estime l'étirement et le rétrécissement de diamètre que le fil souffre lorsqu'un poids de 100 kg-f.

Solution

En premier lieu, il est nécessaire de calculer l'effort de traction normal que le poids exerce sur le fil, en suivant cette formule:

Peut vous servir: vecteurs dans l'espace: comment graphiquement, applications, exercices

σl = f / a = f / (π / 4 * d ^ 2)

La force F est de 980 N et la section transversale est:

A = (π / 4 * d ^ 2) = (3 1416/4) * (4 * 10 ^ -3 m) ^ 2 = 1,2566 * 10 ^ -5 m ^ 2

Ensuite, l'effort de traction est:

σl = 980 n / 1 2566 * 10 ^ -5 m ^ 2 = 77.986.000 PA

Calcul de la déformation du fil unitaire

Le module d'élasticité du jeune, désigné par la lettre E, est la constante de proportionnalité dans la loi de Hooke qui relie l'effort normal σl à la déformation unitaire εl:

σl = e εl 

De là, la déformation unitaire longitudinale du fil de cuivre peut être éliminée:

εl = σl / e = 77 986 MPa / 110000 MPa = 7,09 * 10 ^ -4

Calcul de la déformation unitaire transversale

En revanche, pour connaître la déformation unitaire transversale, le coefficient de Poisson est appliqué:

ν = - εt / εl 

Enfin, vous devez transmettre la déformation unitaire est: 

εt = -ν εl = -0,34 * 7.09 * 10 ^ -4 = -2,41 * 10 ^ -4

Calcul de l'étirement absolu du câble

Enfin, pour connaître l'étirement absolu du câble, la relation suivante doit être appliquée:

Δl = εl * l = 7,09 * 10 ^ -4 * 1 m = 7,09 * 10 ^ -4 m = 0,709 mm

C'est-à-dire avec ce poids, le câble a à peine étiré 0,709 millimètre.

Calcul de la diminution du diamètre

Pour obtenir un rétrécissement absolu de diamètre, nous utilisons la formule suivante:

Δd = εt * d = -2,41 * 10 ^ -4 * 4 mm = -9,64 * 10 ^ -4 mm = -0 000964 millimètres.

Ce rétrécissement en diamètre est si petit qu'il est difficile à apprécier à l'œil nu, même sa mesure nécessite un instrument de haute précision.

Les références

1. Bière f ... mécanique des matériaux. 5e. Édition. 2010. Mc Graw Hill. 1-130.
2. Hibbeler R. Mécanique des matériaux. Huitième édition. Prentice Hall. 2011. 3-60.
3. GERE J. Mécanique des matériaux. Huitième édition. Cengage Learning. 4-220.
4. Giancoli, D. 2006. Physique: principes avec applications. 6 ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Notes de physique générale. Unam. 87-98.