Comment obtenir le pourcentage? Exemples et exercices

Il se peut obtenir un pourcentage Avec plusieurs méthodes. Vous pouvez rapidement calculer 10% de n'importe quel nombre uniquement lorsque vous déplacez votre virgule décimale une position à gauche. Par exemple, 10% de 100 est de 10; 10% de 1000 est 100.

Si vous souhaitez calculer des pourcentages plus complexes tels que 36% de 25 ou 250% de 20, d'autres méthodes sont nécessaires. Pour les cas où le système de 10% n'est pas applicable, les méthodologies suivantes peuvent être prises en compte.

Figure 1. Remises avec différents pourcentages. Combien nous sauvons-nous les uns les autres?. Source: Pixabay.

Le terme pourcentage signifie une certaine partie de chaque cent et se réfère à l'opération arithmétique qui est effectuée pour trouver cette partie. Par exemple, 20% («vingt pour cent») sont lus en pesos, cela signifie que 20 pesos sont réduits pour 100 pesos.

Le pourcentage sert à calculer quelle partie du total représente un montant. Dans ce cas, le total est adopté à l'échelle de 100 et le pourcentage informe la quantité, basée sur ces 100, la partie qui doit être calculée.

Voyons comment cela se fait avec ces exemples. En premier lieu, nous le faisons sous la forme d'une fraction:

• 20% = 20/100
• 5% = 5/100
• 0,7% = 0,7 / 100
• 100% = 100/100

Notez que 100% est égal à 1. Mais les pourcentages peuvent également être écrits décimaux:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Lorsque le pourcentage d'un certain nombre est exprimé, La virgule bouge De ces deux endroits à gauche. En pourcentage, le règle de proportionnalité:

20% est donc 20 sur 100:

20% de 100 est de 20, 20% de 200 est de 40, 20% de 300 est de 60, 20% de 50 est 10.

Règle générale pour 20% de tout montant

20% de x est x * (20/100) = x * 0,2 = 0,2 * x

Cette règle peut facilement s'étendre pour trouver tout autre pourcentage souhaité. Voyons comment dans la section suivante.

Exercice résolu avec la formule pour calculer n% 

Une formule pour résumer dès que possible et calculer rapidement tout pourcentage n est:

n% =(A * n) / 100

Par exemple, vous souhaitez calculer 25% de 400

Alors n = 25 et a = 400, résultant en (400 * 25) / 100 = 100

Exemple

Quel pourcentage de 60 est 24?

Solution

Ce qui est demandé équivaut à demander quel est le n% de 60 qui donne 24?

Nous proposons la formule générale:

60 * n / 100 = 24

Nous effacer n Avec cette procédure:

-Le 100 qui se divise en membre iZiédo D'égalité, allez au membre droite multiplication. 

-Et le 60 qui se multiplie dans le membre gauche Aller chez le membre droite partage.

N = 24 * 100/60 = 2400/60 = 240/6 = 6 * 40/6 = 40

Il est conclu que 40% de 60 est 24.

Exercices de calcul en pourcentage résolu 

Vous trouverez ci-dessous des exercices simples pour commencer à pratiquer le.

Il peut vous servir: les 15 légendes et mythes les plus populaires

Exercice 1

Trouvez 50% de 90.

Solution

Ici x = 90, n = 50% et remplacer:

90 * 50% = 90 * (50/100) = 4500/100 = 45 

C'est assez simple, car 50% de tout montant est la moitié de ce montant et la moitié de 90 est 45.

Exercice 2

Trouvez 30% de 90.

Solution

90 * 30% = 90 * (30/100) = 2700/100 = 27

Pourcentage d'augmentation

Il est fréquent dans la vie quotidienne d'écouter l'augmentation de quelque chose, par exemple une augmentation de la production, une augmentation de salaire ou l'augmentation d'un produit. Il est presque toujours exprimé sous forme de pourcentage.

Par exemple, un certain produit coûte 300 € mais a subi une augmentation de 30%. Nous nous demandons: quel est le nouveau prix du produit?

La première consiste à calculer la partie qui correspond à l'augmentation. Comme l'augmentation est de 30 parties de 100, donc l'augmentation de l'augmentation, basée sur le prix d'origine de 300, est trois fois les 30 parties, soit 3 * 30 = 90.

Le produit a augmenté de 90 €, donc le nouveau prix final sera ce qui a coûté l'augmentation avant:

Nouveau prix = ancien prix + 90 € = 390 €

Nous pouvons construire une formule pour le calcul du pourcentage d'augmentation. Nous utilisons des lettres pour symboliser les prix, comme ceci:

-F est la valeur finale

-Toi est la valeur initiale et

-n L'augmentation de l'augmentation.

Avec ces noms, la valeur finale serait calculée comme ceci:

f = i + (i * n / 100)

Mais comment Toi Il se répète dans les deux termes, il peut être considéré comme un facteur communPour obtenir cette autre expression, également valide:

F = i * (1 + n / 100)

Vérinons avec l'affaire déjà résolue, le produit qui coûte 300 € et a augmenté de 30%. Ainsi, nous nous assurons que la formule fonctionne bien:

Prix ​​final = F = 300 € * (1 + 30/100) = 300 € * (1 + 0,3) = 300 € * 1,3 = 390 €

Exercice 3

Un employé a gagné 1500 €, mais a été promu et son salaire a connu une augmentation de 20%. Quel est votre nouveau salaire?

Solution

Appliquons la formule:

F = 1500 € * (1 + 20/100) = 1500 € * (1 + 0,2) = 1500 € * 1,2 = 1800 €

Le nouveau salaire des employés est de 1800 €.

Pourcentage diminue

En cas de diminution, la formule du calcul de la valeur finale F d'un certain montant initial Toi qui a subi une diminution de n% est:

F = i * (1 - n / 100)

Il convient de noter que le signe positif (+) de la formule dans la section précédente a été remplacé par un signe négatif (-).

Figure 2. Avis de réduction en pourcentage. Source: Pixabay

Exercice 4

Un produit marqué 800 €, mais a reçu une remise de 15%. Quel est le nouveau prix du produit?

Solution 4

Le prix final selon la formule est:

F = 800 € * (1 - 15/100) = 800 € * (1 - 0,15) = 800 € * (0,85) = 680 €

Le prix final avec la remise de 15% est de 680 €, ce qui représente une économie de 120 €.

Pourcentages successifs

Il apparaît quand un montant subit une variation en pourcentage, puis un autre est appliqué, également un pourcentage. Par exemple, un produit qui a eu deux rabais en pourcentage consécutifs. Un autre exemple est celui d'un employé qui avait deux augmentations de salaire consécutives.

Peut vous servir: activités économiques du Yucatan plus importantes

- Pourcentage successif augmente

La base de la solution de ces cas est la même que les augmentations uniques, mais il faut tenir compte que la deuxième augmentation en pourcentage est effectuée sur la valeur finale de la première augmentation.

Supposons un produit qui a augmenté en premier 10% puis 5%. Il est incorrect de dire qu'il a subi une augmentation de 15%, c'était en fait plus que ce pourcentage.

Les formules de la valeur finale s'appliqueraient comme ceci:

-D'abord, la valeur finale de la première augmentation de N1% est calculée

f1 = i + i * n1 / 100

-Et puis, pour trouver la valeur finale de la deuxième augmentation de N2%, la valeur finale de F1 est considérée comme une valeur initiale. Donc:

F2 = f1 + f1 * n2 / 100 

Exercice 5

Un livre a coûté à l'origine 55 €, mais en raison de son succès et de sa forte demande, il a subi deux augmentations consécutives du prix d'origine. La première augmentation était de 10% et la seconde de 20%. Quel est le prix final du livre?

Solution

-Première augmentation:

F1 = 55 € * (1 + 10/100) = 55 € * 1,1 = 60,5 €

-Deuxième augmentation

F2 = 60,5 € * (1 + 20/100) = 60,5 € * 1,2 = 72,6 €

Le prix final est de 72,6 €.

Exercice 6

En référence à l'exercice précédent. Les deux augmentations consécutives: à quel pourcentage d'une augmentation unique par rapport au prix du livre d'origine correspond?

Solution

Si nous appelons N% au pourcentage d'augmentation unique, la formule qui relie cette augmentation unique à la valeur d'origine et à la valeur finale est:

F2 = i * (1 + n / 100) 

C'est-à-dire:

72,6 € = 55 € + 55 € * (n / 100)

Effacement de l'augmentation de l'augmentation N% = (n / 100), nous avons:

(N / 100) = (72,6 € - 55 €) / 55 € = 17.6 / € 55 € = 0,32

Donc:

N = 0,32 * 100 = 32

Au prix du livre, une augmentation totale de 32% a été appliquée. Notez que cette augmentation est supérieure à la somme des deux augmentations de pourcentage consécutives.

- Remises successives en pourcentage

L'idée est similaire à celle des augmentations de pourcentage successives. Le deuxième pourcentage de rabais doit toujours être appliqué à la valeur finale de la première remise, examinons un exemple:

Exercice 7

Une remise de 10% suivie d'une deuxième remise de 20% sur un objet, à laquelle le pourcentage de rabais unique est équivalent?

Solution

-Première remise:

F1 = i - i * n1 / 100  

-Deuxième remise

F2 = f1 - f1 * n2 / 100

Remplacement de la première équation dans le second restes:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Développer cette expression, nous obtenons:

f2 = i - i * n1 / 100 - i * n2 / 100 + i * (n1 / 100) (n2 / 100) 

Dessin de facteur commun Toi:

f2 = i * (1- n1% - n2% + n1% * n2%)

Enfin, les pourcentages indiqués dans la question sont remplacés:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100/100) = i * (1 - 28%)

En d'autres termes, les remises successives de 10% et 20% correspondent à une remise unique de 28%.

Exercices avancés

Essayons ces exercices uniquement lorsque les idées des précédentes ont été suffisamment claires.

Il peut vous servir: couvertures de géographie faciles et belles, couvertures, images

Exercice 8

La base d'un triangle mesure 10 cm et une hauteur 6 cm. Si la longueur de base diminue de 10%. En quel pourcentage la hauteur doit-elle être augmentée de sorte que la zone du triangle ne change pas?

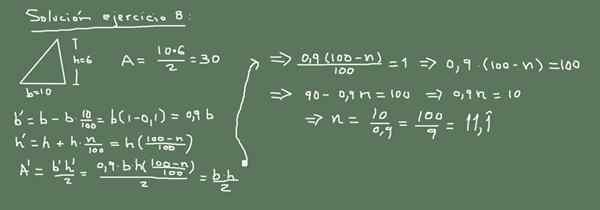figure 3. Solution alternative à l'exercice 8. Préparé par f. Zapata.

Solution 8

La zone du triangle d'origine est:

A = (10cm * 6cm) / 2 = 30 cm²

Maintenant, si la base diminue de 10%, sa nouvelle valeur est:

Nouvelle base = 10 - (10/100) x 10 = 9 cm.

La nouvelle valeur de hauteur sera x, et la zone d'origine doit être maintenue inchangée, de sorte que:

(9cm * x) / 2 = 30 cm²

Ensuite, la valeur de x est effacée comme:

X = 60 cm² / 9 cm = (20/3) cm = 6 666 cm

Ce qui signifie une augmentation de 0,666 par rapport à la valeur d'origine. Voyons maintenant quel pourcentage de cela représente:

6 666 = 6 + (6 * n / 100) 

6 666 -6 = 6 * n / 100

0.666 = 6 * n / 100

N / 100 = 0,111

N = 11,1

La réponse est: la hauteur doit être augmentée de 11,1% pour que la zone du triangle reste la même.

Exercice 9

Si le salaire est augmenté de 20%, mais que l'impôt réduit de 5%, quelle est la véritable augmentation que le travailleur reçoit?

Solution 

Nous calculons d'abord l'augmentation de N1%:

f1 = i + i * n1 / 100

Ensuite, nous appliquons la réduction N2%:

F2 = f1 - f1 * n2 / 100

La première équation est remplacée dans la seconde:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

L'expression précédente se développe:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Enfin, il est supprimé Toi Le facteur commun et les valeurs de n1 = 20 et n2 = 5 qui apparaissent dans l'instruction sont remplacées:

F2 = i (1 + 0,2 - 0,05 - 0,2 * 0,05) = i * (1 + 7/50) = i * (1 + 14/100) = i * (1 + 14%)

Le travailleur a reçu une augmentation nette de 14%.

Exercice 10

Décidez ce qui est le plus pratique entre ces deux options:

i) Acquérir des shirts en T avec une remise de 32%.

Ii) Achetez 3 shirts T pour le prix de 2.

Solution 

Nous analysons chaque option séparément, puis choisissons les plus économiques: nous analysons:

i) Soit X le prix actuel d'une chemise, une remise de 32% représente un prix final de XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Par exemple, acheter 3 chemises signifie dépenser 3 x 0.68 x = 2.04X

ii) Si x est le prix d'une chemise, pour 3 chemises, vous paierez simplement 2x.

Supposons qu'une chemise vaut 6 euros, avec la remise de 32%, elle vaut 4.08 euros. Acheter 1 T -Shirt n'est pas une option valide dans l'offre 3 × 2. Donc, si vous voulez seulement acheter 1 chemise, la remise est préférable.

Mais si ce que vous voulez, c'est acheter pour des dizaines, l'offre 3 × 2 est juste un peu moins chère. Par exemple, 6 t-shirts avec le rabais se dérouleraient pour 24.48 euros, tandis qu'avec l'offre 3 × 2, ils coûteraient 24 euros

Les références

1. Salle de classe facile. Le pourcentage. Récupéré de: salle de classe.com
2. Baldor a. 2006. Arithmétique théorique pratique. Éditions culturelles.
3. Education Kids. Comment apprendre à calculer les pourcentages. Récupéré de: educapeques.com
4. Guérrez, g. Notes de mathématiques financières. Récupéré de: csh.Izt.Uam.mx
5. Ticks intelligents. Pourcentage: ce qui est et comment est calculé. Récupéré de: Smartick.est