Montants vectoriels

Quelles sont les montants vectoriels?

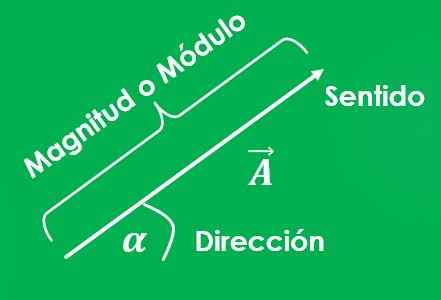
Le Quantité vectorielle, ou vecteur, comme celui pour lequel il est nécessaire de spécifier à la fois sa magnitude ou son module (avec les unités respectives) et leur adresse.

Contrairement à la quantité vectorielle, une quantité scalaire n'a que de la magnitude (et des unités), mais pas d'adressage. Quelques exemples de quantités scalaires sont la température, le volume d'un objet, la longueur, la masse et le temps, entre autres.

Différence entre la quantité vectorielle et l'escalade

Dans l'exemple suivant, vous pouvez apprendre à différencier une quantité scalaire d'une quantité vectorielle:

Une vitesse de 10 km / h est une quantité scalaire, tandis qu'une vitesse de 10 km / h au nord est une quantité vectorielle. La différence est que dans le deuxième cas, une adresse est spécifiée, en plus de l'amplitude.

Les quantités vectorielles ont une infinité d'applications, en particulier dans le monde de la physique.

Graphiques et dénotations d'une quantité vectorielle

Le moyen de désigner un montant vectoriel est de placer une flèche (→) sur la lettre à utiliser, ou d'écrire la lettre en gras (pour).

Pour représenter une quantité de vecteur, un système de référence est nécessaire. Dans ce cas, le plan cartésien sera utilisé comme système de référence.

Le graphique d'un vecteur est une ligne dont la longueur représente la magnitude; et l'angle entre ladite ligne et l'axe x, mesuré au sens anti-respect, représente son adresse.

Il faut spécifier quel est le point de départ du vecteur et quel est le point d'arrivée. Une flèche est également placée à la fin de la ligne qui pointe vers le point d'arrivée, ce qui indique quelle est la direction du vecteur.

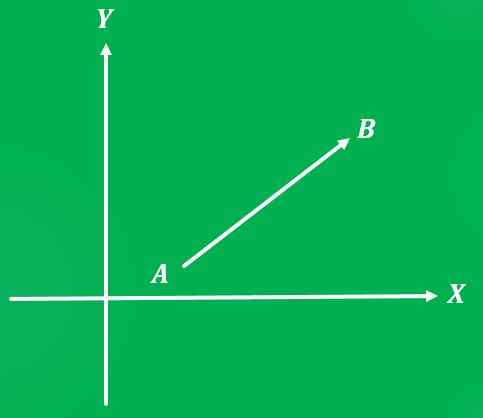
Une fois qu'un système de référence est défini, vous pouvez écrire le vecteur en tant que paire ordonnée: la première coordonnée représente sa magnitude et la deuxième coordonnée son adresse.

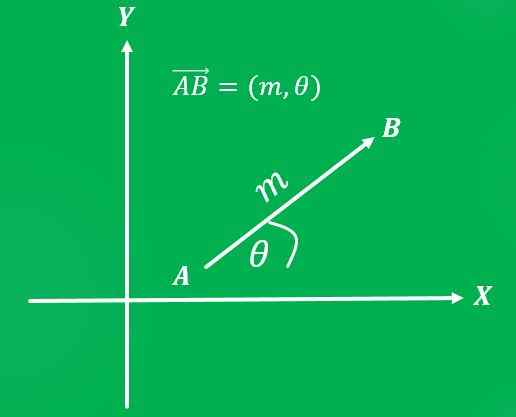
Exemples de montants vectoriels

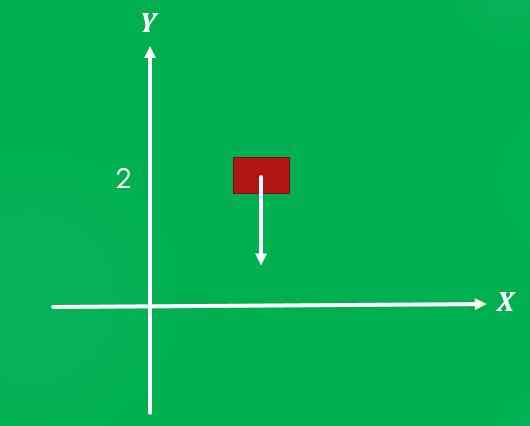
1- Gravité agissant sur un objet

Si un objet est placé à une hauteur de 2 mètres au-dessus du sol et qu'il est libéré, la gravité agit dessus avec une ampleur de 9,8 m / s² et une direction perpendiculaire au sol dans la direction.

2- Mouvement d'un avion

Un avion qui se déplaçait du point A = (2,3) au point B = (5,6) du plan cartésien, avec une vitesse de 650 km / h (magnitude). La direction de la trajectoire est de 45 ° au nord-est (signification).

Il convient de noter que, si l'ordre est inversé, le vecteur a la même ampleur et la même direction, mais une signification différente, qui sera au sud-ouest.

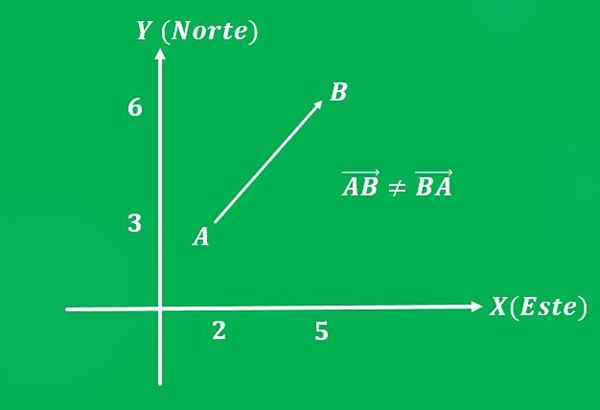
3- Force appliquée à un objet

Juan décide de pousser une chaise avec une force de 10 livres, dans une direction parallèle au sol. Les sens possibles de la force appliquée sont: à gauche ou à droite (dans le cas du plan cartésien).

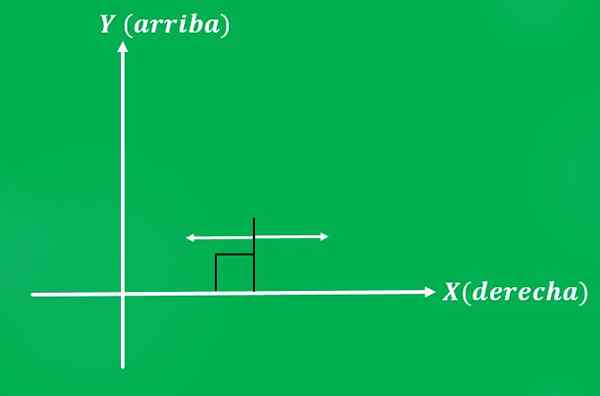
Ainsi que dans l'exemple précédent, le sens que Juan décide de donner la force produira un résultat différent.

Cela nous dit que deux vecteurs peuvent avoir la même ampleur et la même direction, mais être différents (produire des résultats différents).

Deux vecteurs ou plus peuvent être ajoutés et soustraits, pour lesquels il y a des résultats très utiles, comme la loi parallélogramme. Vous pouvez également multiplier un vecteur par un scalaire.