Formules de chaleur parfumés, comment le calculer et résoudre des exercices

Il Cède la chaleur C'est le transfert d'énergie entre deux corps à des températures différentes. Celui qui est une température plus élevée donne de la chaleur à celle dont la température est plus faible. Que le corps cède ou absorbe la chaleur, sa température ou sa condition physique peut varier en fonction de la masse et des caractéristiques du matériau dont il est fabriqué.

Un bon exemple est dans une tasse de café fumant. La cuillère de métal avec laquelle le sucre est agité. S'il est laissé à l'intérieur de la tasse suffisamment de temps, le café et la cuillère à café en métal se termineront. Une certaine chaleur sera passée à l'environnement, car le système n'est pas isolé.

Le café et la cuillère à café deviennent en équilibre thermique pendant un certain temps. Source: Pixabay.

Lorsque les températures sont appariées, le équilibre thermique.

Si le même test était effectué avec une cuillère à café en plastique, il remarquerait sûrement qu'il ne chauffe pas aussi vite que le métal, mais finalement il deviendra également en équilibre avec le café et tout ce qui l'entoure.

C'est parce que le métal mène la chaleur mieux que le plastique. D'un autre côté, le café donne sûrement de la chaleur à un rythme différent de celui du chocolat chaud ou d'une autre boisson. Ensuite, la chaleur affectée ou absorbée par chaque objet dépend du matériau ou de la substance.

[TOC]

Qu'est-ce que et les formules

La chaleur fait toujours référence à l'écoulement ou au transit d'énergie entre un objet et un autre, en raison de la différence de température.

C'est pourquoi il est question de chaleur de chaleur ou de chaleur absorbée, car en ajoutant ou en extrayant de la chaleur ou de l'énergie d'une manière ou d'une autre, il est possible de modifier la température d'un élément.

Il est généralement appelé la quantité de chaleur que l'objet le plus chaud donne. Cette valeur est proportionnelle à la masse dudit objet. Un corps avec une grande masse est capable d'abandonner plus de chaleur qu'un autre de la masse moindre.

Peut vous servir: Expérience Millikan: procédure, explication, importance

La différence de température Δt

Un autre facteur important dans le calcul de la chaleur attribuée est la différence de température que l'objet qui donne la chaleur éprouve. Il est désigné comme δT Et il est calculé comme ceci:

Δt = t_F - T_soit

Enfin, la quantité de chaleur attribuée dépend également de la nature et des caractéristiques de l'objet, qui sont résumées quantitativement dans une constante appelée Chaleur de chaleur spécifique, indiqué c.

Ainsi, l'expression de la chaleur attribuée est la suivante:

Q_Scèsement = - m.c.ΔT

Le rendement est symbolisé par un signe négatif.

La chaleur et la capacité de chaleur spécifiques d'une substance

La chaleur spécifique est la quantité de chaleur nécessaire pour augmenter la température de 1 g de substance de 1 ° C. C'est une propriété intrinsèque du matériel. Ses unités dans le système international sont: Joule / kg . K (Joule entre la température du kilogramme x en degrés Kelvin).

La capacité thermique C est un concept lié, mais légèrement différent, car la masse de l'objet intervient. La capacité thermique est définie comme suit:

C = MC

Ses unités en s.Toi. Ils sont Joule / K. Afin que la chaleur cédée puisse également être exprimée de manière équivalente comme:

Q = -C. ΔT

Comment le calculer?

Pour calculer la chaleur attribuée par un objet, il est nécessaire de connaître ce qui suit:

- La chaleur spécifique de la substance qui donne la chaleur.

- La masse de ladite substance

- La température finale à obtenir

Les valeurs de chaleur spécifiques pour de nombreux matériaux ont été déterminées expérimentalement et sont disponibles dans des tables.

Calorimétrie

Maintenant, si cette valeur n'est pas connue, il est possible de l'obtenir à l'aide d'un thermomètre et d'eau dans un récipient thermiquement isolé: le calorimètre. Un schéma de cet appareil est illustré dans la figure qui accompagne l'exercice 1.

Un échantillon de la substance est immergé à une certaine température dans une quantité d'eau qui a précédemment mesuré. La température finale est mesurée et avec les valeurs obtenues, la chaleur spécifique du matériau est déterminée.

Peut vous servir: erreur aléatoire: formule et équations, calcul, exemples, exercices

En comparant le résultat avec des valeurs tabulées, il peut être connu de quelle substance il s'agit. Cette procédure est appelée calorimétrie.

L'équilibre thermique est effectué par la conservation de l'énergie:

Q _Scèsement + Q _{absorbé = 0}

Exercices résolus

Exercice 1

Un morceau 0 de 0.35 kg à une température de 150 ºC dans 500 ml d'eau à une température de 25 º C. Trouver:

a) la température d'équilibre finale

b) Combien de chaleur coule dans ce processus?

Données

c_cuivre = 385 J / kg . ºC

c_{eau =} 4180 J / kg . ºC

Densité d'eau: 1000 kg / m³

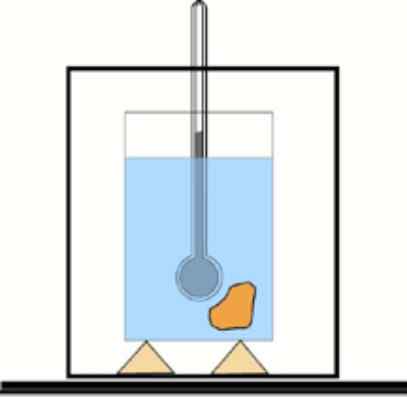Schéma de calorimètre de base: un récipient avec de l'eau isolée et un thermomètre pour mesurer les changements de température. Lficient: Dr. Tilahun Tesfaye [cc by-sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Solution

a) Le cuivre donne de la chaleur pendant que l'eau l'absorbe. Comme le système est considéré comme fermé, seuls l'eau et l'échantillon interviennent dans le bilan thermique:

Q _Scèsement = Q _absorbé

En revanche, il est nécessaire de calculer la masse de 500 ml d'eau:

500 ml = 0.5 L = 0.0005 m³

Avec ces données, la masse de l'eau est calculée:

masse = densité x volume = 1000 kg / m³ . 0.0005 m³ = 0.5 kg

L'équation thermique est soulevée dans chaque substance:

Q_Scèsement = -m_cuivre . c_cuivre. ΔT = -0.35 kg . 385 J / kg .ºC . (T_F -150 ºC) = -134.75 (t_F - 150) J

Q_absorbé = m_eau . c_eau. ΔT = 0.5 kg . 4186 J / kg . ºC .(T_F -25 ºC) = 2093 (t_F -25) J        

Égalisant les résultats que vous avez:

2093 (t_F - 25) = -134.75 (t_F - 150)

Il s'agit d'une équation linéaire avec une inconnue, dont la solution est:

T_F = 32.56 ºC

b) La quantité de chaleur coulant est la chaleur attribuée ou la chaleur absorbée:

Q _Scèsement = - 134.75 (32.56 - 150) J = 15823 J

Q _absorbé = 2093 (32.56 - 25) J = 15823 J

Exercice 2

Une pièce de cuivre de 100 g est chauffée dans un four à une température t_soit Puis il est introduit dans un calorimètre de cuivre de 15 g qui contient 200 g d'eau à 16 º C. La température finale une fois en équilibre est de 38 º C. Lorsque le calorimètre et son contenu sont pesés, il est constaté que j'ai évaporé.2 g d'eau quelle était la température initiale t_soit?

Peut vous servir: trou de ver: histoire, théorie, types, formation

Données: La chaleur latente de la vaporisation de l'eau est L_V = 2257 kJ / kg

Solution

Cet exercice diffère de la précédente, car il faut considérer que le calorimètre absorbe également la chaleur. La chaleur attribuée par la pièce en cuivre est investie dans toutes les éléments suivants:

- Chauffer l'eau du calorimètre (200 g)

- Chauffer le cuivre dont le calorimètre est fabriqué (150 g)

- Évaporer 1.2 grammes d'eau (pour un changement de phase, vous avez également besoin d'énergie).

Q_Scèsement = -100 X 1 x 10 ^-3 kg. 385 J / kg . ºC. (38 - t_soit ) ºC = -38.5. (38 - t_soit) J

Q _{absorbé par lui calorimètre} = Q _{absorbé par l'eau} + Q _vaporisation + Q _{absorbé par le cuivre}

0.2 kg .4186 J / kg ºC .(38 - 16 ºC) + 1.2 x 10^-3 kg. 2257000 J / kg +0.150 kg .385 J / kg .ºC.(38 - 16 ºC) =

18418.4 +2708.4 + 1270.5 J = 22397.3 J

Donc:

-38.5. (38 - t_soit) = 22397.3

T_soit = 619.7 ºC

La chaleur nécessaire pour transporter le 1 aurait également pu être considérée.2 g d'eau jusqu'à 100 º C, mais c'est une quantité assez petite comparée.

Les références

1. Giancoli, D.  2006. Physique: principes avec applications. 6^e. Élégant. Prentice Hall. 400 - 410.
2. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 156 - 164.
3. Rex, un. 2011. Fondamentaux de la physique. Pearson. 309 - 332.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14^e. Élégant. Volume 1. 556 - 553.
5. SERAY, R., Vulle, c. 2011. Fondamentaux de la physique. 9^{n / A} Cengage Learning.