Définition de plate-forme factorielle, formules et exercices

Il Plate-forme factorielle C'est une machine simple qui se compose d'un arrangement de poulies avec un effet de force multiplicateur. De cette façon, vous pouvez augmenter une charge en appliquant juste l'équivalent d'une fraction du poids à l'extrémité libre de la corde.

Il se compose de deux ensembles de poulies: une qui est fixée à un support et une autre qui exerce la force résultante sur la charge. Les poulies sont montées sur un cadre généralement métallique qui les tient. 

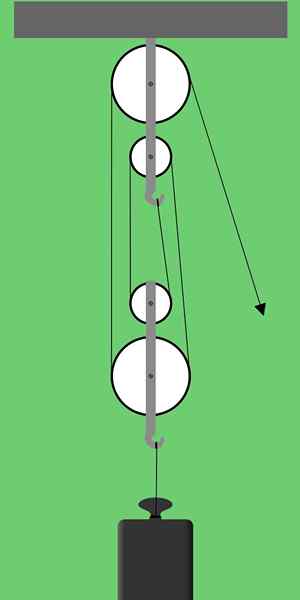
Figure 1. Schéma d'une plate-forme factorielle. Source: Pixabay

La figure 1 montre une plate-forme factorielle qui se compose de deux groupes de deux poulies chacune. Ce type de dispositions de poulie est également appelée Gréement de la série soit Polypastes.

[TOC]

Formules de droite factorielle

Cas 1: une poulie mobile et un

Pour comprendre pourquoi cet arrangement multiplie la force exercée, nous commencerons par le cas le plus simple, composé d'une poulie fixe et mobile.

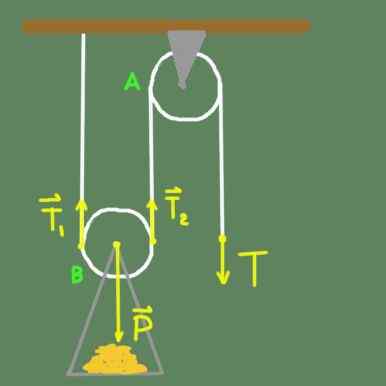Figure 2. Two Poulle.

Dans la figure 2, nous avons une poulie fixe sur le toit par soutien. Poulie a peut tourner librement autour de son axe. Nous avons également une poulie B qui a un support fixe à l'axe de la poulie, dans lequel la charge est placée. La poulie B, en plus de pouvoir tourner librement autour de son axe, a la possibilité de se déplacer verticalement.

Supposons que nous soyons dans une situation d'équilibre. Considérez les forces agissant sur la poulie B. L'axe B -pullley prend en charge un poids total P qui est dirigé vers le bas. Si c'était la seule force sur la poulie B alors, mais nous savons que la corde qui traverse cette poulie exerce également deux forces, qui sont les T1 et T2 qui sont dirigés vers le haut.

Pour l'équilibre translationnel, les deux forces doivent être les mêmes au poids qui soutient l'axe de la poulie B.

T1 + t2 = p

Mais comme la poulie B est également en équilibre de rotation, alors t1 = t2. Les forces T1 et T2 proviennent de la tension appliquée à la corde, appelée t.

Il peut vous servir: modèle atomique bohr

Donc t1 = t2 = t. Le remplacement de l'équation précédente reste:

T + t = p

2T = P

Indiquant que la tension appliquée à la corde n'est que la moitié du poids:

T = p / 2

Par exemple, si la charge était de 100 kg, il serait suffisant pour appliquer une force de 50 kg à l'extrémité libre de la corde pour augmenter la charge à vitesse constante.

Cas 2: deux poulies mobiles et deux

Examinons les tensions et les forces qui agissent sur un ensemble qui se compose de deux supports des supports A et B avec deux poulies chacune.

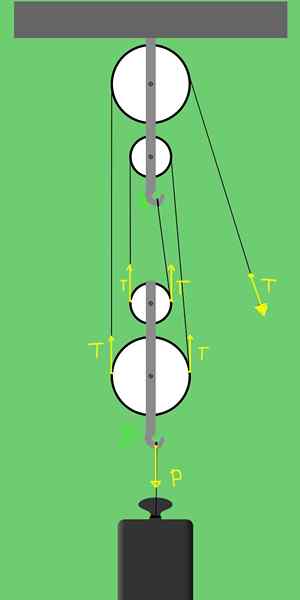figure 3. Forces sur une plate-forme de 2 poulies fixes et 2 poulies mobiles.

Le soutien B a la possibilité de se déplacer verticalement et les forces agissant sur le fils:

- Le poids p de la charge, qui pointe verticalement.

- Deux tensions sur la grande poulie et deux tensions sur la petite poulie. Au total, quatre tensions, toutes pointant vers le haut.

Pour qu'il y ait un équilibre translationnel, il est nécessaire que les forces qui pointent verticalement vers le haut égal à la charge qui pointe vers le bas. C'est-à-dire qu'il doit être accompli:

T + t + t + t = p

C'est-à-dire 4 t = p

D'où il s'ensuit que la force appliquée t à l'extrémité libre de la corde n'est qu'un quart du poids en raison de la charge qui veut augmenter., T = p / 4.

Avec cette valeur pour la tension t, la charge peut être maintenue statique ou augmentant à une vitesse constante. Si une plus grande tension était appliquée que cette valeur, la charge s'accélérerait, une condition nécessaire pour le retirer du reste.

Case générale: n Puleys mobiles et n poulies fixes

Comme le montre les cas précédents, pour chaque poulie de l'ensemble mobile, il y a quelques forces vers le haut par la corde qui passe à travers la poulie. Mais cette force ne peut être autre chose que la tension appliquée à la corde à l'extrémité libre.

Donc, pour chaque poulie mobile, il y aura une force ascendante qui vaut 2T. Mais comme il y a n poulies dans l'ensemble mobile, il est alors nécessaire de souligner verticalement vers le haut est:

Peut vous servir: moteur à cage d'écureuil

2 N T

Pour l'équilibre vertical, il est nécessaire que:

2 n t = p

Par conséquent, la force appliquée à l'extrémité libre est:

T = p / (2 n)

Dans ce cas, on peut dire que la force exercée t se multiplie 2 n fois sur la charge.

Par exemple, si nous avions une plate-forme factorielle de 3 poulies fixes et 3 mobiles, le nombre N serait égal à 3. D'un autre côté, si la charge était p = 120 kg, alors la force appliquée à l'extrémité libre serait t = 120 kg / (2 * 3) = 20 kg.

Exercices résolus

Exercice 1

Considérez une plate-forme factorielle composée de deux poulies fixes et de deux poulies mobiles. La tension maximale qui peut supporter la corde est de 60 kg. Déterminez quelle est la charge maximale qui peut être placée.

Solution

Lorsque la charge est au repos ou en se déplaçant constamment le poids de celui-ci, il est lié à la tension T appliquée dans la corde au moyen de la relation suivante:

P = 2 n t

Comme c'est une plate-forme de deux poulies mobiles et deux poulies fixes, alors n = 2.

La charge maximale qui peut être placée est obtenue lorsque t a la valeur maximale possible, qui dans ce cas est de 60 kg.

Charge maximale = 2 * 2 * 60 kg = 240 kg

Exercice 2

Trouvez la relation entre la tension de la corde et le poids de la charge, dans une plate-forme factorielle de deux poulies dans lesquelles la charge accélère avec accélération à.

Solution

La différence dans cet exemple concernant ce qui a été vu jusqu'à présent est que la dynamique du système doit être considérée. Nous proposons donc la deuxième loi de Newton pour trouver la relation demandée.

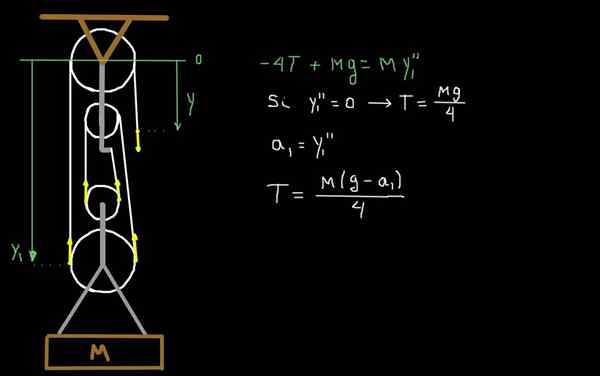Figure 4. Dynamique de la plate-forme factorielle.

Dans la figure 4, nous dessinons les forces en raison de la tension t de la corde. La partie mobile de la plate-forme a une masse totale m. Nous prenons en tant que système de référence au niveau de la première poulie fixe et positive.

Y1 est la position de l'axe de poulie la plus basse.

Nous appliquons la deuxième loi de Newton pour déterminer l'accélération A1 de la partie mobile de la plate-forme:

Peut vous servir: théorème de varignon

-4 t + mg = m a1

Comme le poids de la charge est p = mg, où g est l'accélération de la gravité, la relation précédente peut être écrite:

-4T + P = P (A1 / G)

Si nous voulions déterminer la tension appliquée dans la corde lorsqu'une certaine charge de poids est accélérée avec l'accélération A1, la relation précédente serait comme ceci:

T = p (1 - a1 / g) / 4

Notez que si le système était au repos ou se déplaçait constamment, alors a1 = 0, et que nous avons récupéré la même expression que nous avons obtenue dans le cas 2.

Exercice 3

Dans cet exemple, le même plate-forme d'exercice 1 est utilisé, avec la même corde qui prend en charge un maximum de 60 kg de tension. Une certaine charge augmente, l'accélérant du repos à 1 m / s par 0,5 s, en utilisant la tension maximale de la corde. Trouvez le poids de charge maximum.

Solution

Nous utiliserons les expressions obtenues dans l'exercice 2 et le système de référence de la figure 4 dans laquelle l'adresse positive est verticale en bas.

L'accélération de la charge est a1 = (-1 m / s -0 m / s) /0,5 s = -2 m / s ^ 2.

Le poids de la charge en kilogramme-force est donné par

P = 4 t / (1 - a1 / g)

P = 4 * 60 kg / (1 + 2/9.8) = 199,3 kg

C'est le poids maximal possible de la charge sans que la corde soit cassée. Notez que la valeur obtenue est inférieure à celle obtenue dans l'exemple 1, dans lequel la charge était supposée avec une accélération nulle, c'est-à-dire au repos ou à une vitesse constante.

Les références

1. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. 101-120.
2. Resnick, r. (1999). Physique. Vol. 1. 3 RA ED. en espagnol. Société de rédaction continentale S.POUR. de c.V. 87-103.
3. Giancoli, D. 2006. Physique: principes avec applications. 6e. Élégant. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Sciences physiques conceptuelles. 5e. Élégant. Pearson.38-61.
5. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning. 100 - 119.