Propriétés de base orthormale, exemples et exercices

Ongle Base ortonormale Il est formé avec des vecteurs perpendiculaires les uns avec les autres et dont le module vaut également 1 (vecteurs unitaires). N'oubliez pas qu'une base B dans un espace vectoriel V, Il est défini comme un ensemble de vecteurs linéairement indépendants capables de générer cet espace.

À son tour, un espace vectoriel est une entité mathématique abstraite entre les éléments desquels sont des vecteurs, généralement associés à des amplitudes physiques telles que la vitesse, la force et le déplacement ou également à des matrices, des polynômes et des fonctions.

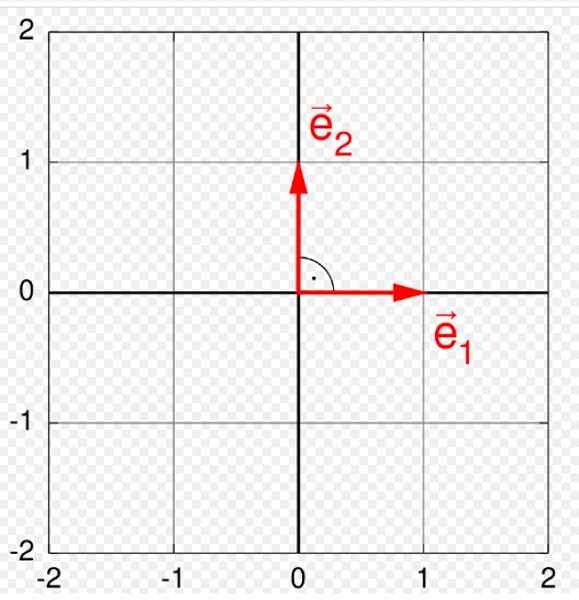
Figure 1. Base orthonormale dans le plan. Source: Wikimedia Commons. Quartl [cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 3.0)].

Les vecteurs ont trois éléments distinctifs: l'ampleur ou le module, la direction et le sens. Une base Ortonormal est particulièrement utile pour représenter et fonctionner avec eux, car tout vecteur qui appartient à un certain espace vectoriel V, Il peut être écrit comme une combinaison linéaire des vecteurs qui forment la base orthormale.

De cette façon, les opérations entre vecteurs, telles que la somme, la soustraction et les différents types de produits définis dans ledit espace sont analysés analytiquement.

Parmi les bases les plus utilisées de la physique figure la base formée par des vecteurs unitaires Toi, J et k représentant les trois directions distinctives de l'espace à trois dimensions: haut, large et profondeur. Ces vecteurs sont également connus sous le nom de Vecteurs canoniques unitaires.

Si, au lieu de cela, des vecteurs sont travaillés sur un avion, cela serait suffisant avec deux de ces trois composantes, tandis qu'un seul.

[TOC]

Bases des propriétés

1- Une base B C'est le plus petit ensemble de vecteurs possibles qui génèrent l'espace vectoriel V.

2- Les éléments de B Ils sont linéairement indépendants.

3- Toute base B d'un espace vectoriel V, permet d'exprimer tous les vecteurs de V En tant que combinaison linéaire de celui-ci et cette forme est unique pour chaque vecteur. Par conséquent un B Il est également connu sous le nom Système de générateur.

4- Le même espace vectoriel V peut avoir différentes bases.

Peut vous servir: force centrifuge: formules, comment elle est calculée, exemples, exercices

Exemples de bases

Ci-dessous plusieurs exemples de bases et de bases orthonormales en général:

La base canonique en ℜ ⁿ

Également appelé base naturelle ou base standard de ℜ ⁿ, Où ℜ ⁿ C'est l'espace N dimensionnel, Par exemple, l'espace à trois dimensions est ℜ ³. À la valeur de n On l'appelle dimension de l'espace vectoriel et dénote comme Dim (v).

Tous les vecteurs qui appartiennent à ℜ ⁿ Ils sont représentés par N-USA Commandé. Pour l'espace ℜⁿ, La base canonique est:

et₁ =; et₂ =; et_n =

Dans cet exemple, nous avons utilisé la notation avec des supports ou des «supports» et audacieux pour les vecteurs unitaires et₁, et₂, et₃..

La base canonique en ℜ³

Vecteurs de famille Toi, J et k Ils admettent cette même représentation et ils suffisent à trois pour représenter les vecteurs en ℜ ³:

Toi =; J =;  k =

Cela signifie que la base peut être exprimée comme suit:

B = ; ;

Pour vérifier qu'ils sont linéairement indépendants, le déterminant formé avec eux est non nul et également égal à 1:

Il doit également être possible d'écrire tout vecteur qui appartient à ℜ ³ Comme une combinaison linéaire d'eux. Par exemple, une force dont les composants rectangulaires sont f_X = 4 n, f_et = -7 n et f_z= 0 N serait écrit sous une forme vectorielle comme suit:

F = N = 4Toi -7J + 0k N.

Donc Toi, J et k faire un système de générateur ℜ ³.

Autres bases Ortonormales en ℜ³

La base standard décrite dans la section précédente n'est pas la seule base orthormale en ℜ³. Ici, nous avons par exemple les bases:

B₁ = ; ;

B₂ = ; ;

Il peut être démontré que ces bases sont orthonormales, pour cela, nous nous souvenons des conditions qui doivent être remplies:

Peut vous servir: optique ondulée

-Les vecteurs qui forment la base doivent être orthogonaux les uns aux autres.

-Chacun d'eux doit être unitaire.

Nous pouvons le vérifier en sachant que le déterminant formé par eux doit être non nul et égal à 1.

Base B₁ C'est précisément celui des coordonnées cylindriques ρ, φ et z, une autre façon d'exprimer des vecteurs dans l'espace.

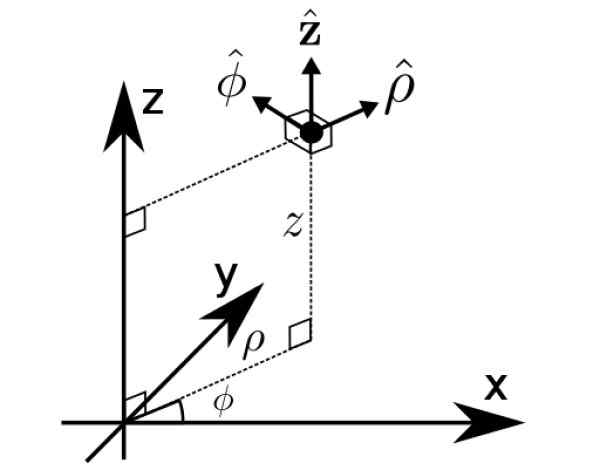Figure 2. Coordonnées cylindriques. Source: Wikimedia Commons. Math Buff [CC By-S (https: // CreenIvecommons.Org / licences / by-sa / 4.0)].

Exercices résolus

- Exercice 1

Montrent que la base b = ; ; est Ortonormal.

Solution

Pour montrer que les vecteurs sont perpendiculaires les uns aux autres, nous utiliserons le produit scalaire, également appelé point interne ou produit de deux vecteurs.

Laissez deux vecteurs ou et V, Votre produit scalaire est défini par:

ou • v = ou.V. cosθ

Pour distinguer les vecteurs de leurs modules, nous utiliserons audacieux pour les premières et normales de lettres pour ce dernier. θ est l'angle entre ou et V, Par conséquent, s'ils sont perpendiculaires, cela signifie que θ = 90º et le produit scalaire est vide.

Alternativement, si les vecteurs sont donnés en termes de composants: ou = X, ou_et,ou_z > et V = X, V_et,V_z >, le produit scalaire des deux, qui est commutatif, est calculé de cette manière:

ou • v = ou_X .V_X + ou_et .V_et + ou_z .V_z

De cette façon, les produits scalaires entre chaque paire de vecteurs sont respectivement:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Pour la deuxième condition, le module de chaque vecteur est calculé, qui est obtenu par:

│u │ = √ (u_X² + ou_et² + ou_z²)

Ainsi, les modules de chaque vecteur sont:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Il peut vous servir: deuxième condition d'équilibre: explication, exemples, exercices

│ = √ [0² + 0²  + 1²)] = 1

Par conséquent, les trois sont des vecteurs unitaires. Enfin, le déterminant qu'ils forment n'est pas nul et égal à 1:

- Exercice 2

Écrivez les coordonnées vectorielles W = En termes de base précédente.

Solution

Pour ce faire, le théorème suivant est utilisé:

Soit b = V₁, V₂, V₃,.. V_n Une base orthonormale dans l'espace V avec produit domestique, le vecteur W Il est représenté par B comme suit:

W = <W•V₁> V₁ + <W•V₂> V₂ +<W•V₃> V₃ +.. <W•V_n> V_n

Cela signifie que nous pouvons écrire le vecteur à la base B, à travers des coefficients <W•V₁>, <W•V₂>, ..  <W•V_n>, pour lequel vous devez calculer les scalaires indiqués:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Avec les produits scalaires obtenus, une matrice est construite, appelée coordonnée de w.

Par conséquent, le vecteur coordonne W Dans la base B, ils sont exprimés à travers:

[W]]_B= [(18/5); (1/5); 1]]

La matrice de coordonnées n'est pas le vecteur, car un vecteur n'est pas le même que ses coordonnées. Ce ne sont qu'un ensemble de nombres qui servent à exprimer le vecteur à une base donnée, pas le vecteur en tant que tel. Ils dépendent également de la base sélectionnée.

Enfin, à la suite du théorème, le vecteur W serait exprimé comme suit:

W = (18/5) V₁ + (1/5) V₂ + V₃

Avec: V₁ =; V₂ =; V₃ =, C'est-à-dire les vecteurs de base B.

Les références

1. Larson, R. Fondamentaux de l'algèbre linéaire. 6e. Édition. Cengage Learning.
2. Larson, R. 2006. Calcul. 7e. Édition. 2ieme volume. McGraw Hill.
3. Salas, J. algèbre linéaire. Sujet 10. Bases Ortonormal. Récupéré de: OCW.Uc3m.est.
4. Université de Séville. Coordonnées cylindriques. Base vectorielle. Récupéré de: Laplace.nous.est.
5. Wikipédia. Base ortonormale. Récupéré de: est.Wikipédia.org.