Concepts d'analyse de maillage, méthodes, exemples

Il Analyse de maillage C'est une technique utilisée pour résoudre des circuits électriques plats. Cette procédure peut également apparaître dans la littérature avec les noms de méthode du courants de circuit o méthode de Courants de maillage (ou boucle).

Les fondements de cette méthodes d'analyse des circuits électriques et d'autres sont dans les lois de la loi de Kirchhoff et d'Ohm. Les lois de Kirchhoff à leur tour sont à leur tour des expressions de deux principes de conservation très importants en physique pour les systèmes isolés: la charge électrique et l'énergie sont préservées.

Figure 1. Les circuits font partie d'innombrables appareils. Source: Pixabay.

D'une part, la charge électrique est liée au courant, qui se déplace la charge, tandis que dans un circuit, l'énergie est liée à la tension, qui est l'agent chargé de faire le travail nécessaire pour maintenir la charge en mouvement.

Ces lois, appliquées à un circuit plat, génèrent un ensemble d'équations simultanées qui doivent être résolues pour obtenir des valeurs de courant ou de tension.

Le système d'équations peut être résolu avec des techniques analytiques déjà connues, telles que Règle de Cramer, qui nécessite le calcul des déterminants pour obtenir la solution système.

Selon le nombre d'équations, ils sont résolus à l'aide d'une calculatrice scientifique ou d'un logiciel mathématique. Sur le réseau, il existe également de nombreuses options disponibles.

[TOC]

Termes importants

Avant d'expliquer comment cela fonctionne, nous commencerons par définir ces termes:

Bifurquer: Section contenant un élément du circuit.

Nœud: point qui relie deux branches ou plus.

Lien: Il s'agit d'une partie fermée d'un circuit, qui commence et se termine par le même nœud.

Engrener: boucle qui ne contient aucune autre obligation à l'intérieur (maillage essentiel).

Méthodes

L'analyse monesale est une méthode générale qui sert à résoudre des circuits dont les éléments sont connectés en série, en parallèle ou mixte, c'est-à-dire lorsque le type de connexion n'est pas clairement distingué. Le circuit doit être plat, ou du moins il doit être possible de le rembourser comme tel.

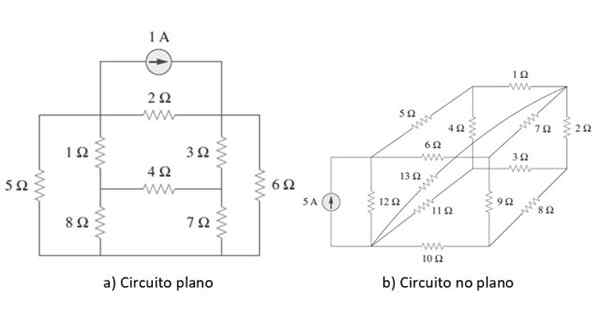Figure 2. Circuits plats et non flat. Source: Alexander, C. 2006. Fondations du circuit électrique. 3e. Édition. Mc Graw Hill.

Un exemple de chaque type de circuit est illustré dans la figure ci-dessus. Une fois le point clarifié, pour commencer, nous appliquerons la méthode à un circuit simple comme exemple dans la section suivante, mais avant de passer brièvement les lois de l'Ohm et de Kirchhoff.

Loi d'Ohm: Sean V La tension, R La résistance e Toi Le courant de l'élément résistif ohmique, dans lequel la tension et le courant sont directement proportionnels, la résistance étant la constante de proportionnalité:

Peut vous servir: Gravité de l'API: échelle et classification du brut

V = i.R

Voltage Kirchhoff Law (LKV): Dans toute trajectoire fermée parcourue dans une direction, la somme algébrique des tensions est nul. Cela comprend des tensions dues aux sources, résistances, inductances ou condensateurs: ∑ E = ∑ R_Toi. Toi

Kirchhoff du courant (LKC): Dans n'importe quel nœud, la somme algébrique des courants est nul, en tenant compte que les courants qui entrent se voient attribuer un panneau et à lequel un autre sort. De cette façon: ∑ i = 0.

Avec la méthode des courants de maillage, il n'est pas nécessaire.

- Étapes pour appliquer l'analyse du maillage

Nous allons commencer à expliquer la méthode pour un circuit de 2 mailles. La procédure peut être prolongée plus tard pour des circuits plus grands.

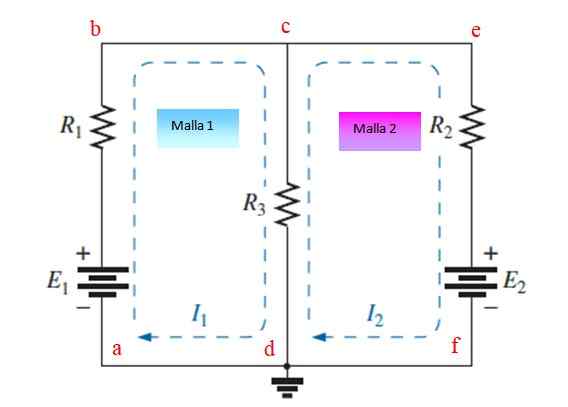figure 3. Circuit avec résistances et sources disposées en deux mailles. Source: F. Zapata.

Étape 1

Attribuer et dessiner des courants indépendants à chaque maillage, dans cet exemple, ils sont Toi₁ et Toi₂. Ils peuvent être tirés dans un calendrier ou aussi anti-horaire.

Étape 2

Appliquez la loi Kirchhoff Tensions (LTK) et la loi d'Ohm à chaque maillage. Les chutes potentielles se voient attribuer un signe (-) tandis que les augmentations se voient attribuer Signe (+).

ABCDA Mesh

En partant du point A et en suivant la signification du courant, nous trouvons une augmentation du potentiel de la batterie E1 (+), puis une baisse de R₁ (-) Et puis une autre chute en r₃ (-).

Simultanément, la résistance r₃ Il est également traversé par le courant i₂, Mais dans la direction opposée, il représente donc une augmentation (+). La première équation est comme ceci:

ET₁-R₁.Toi₁ -R₃.Toi₁ + R₃.Toi₂ = 0

Les termes immédiatement prise en compte et en ré-promenant:

- (R₁+R₃) Yo₁ +R₃Toi₂ = -E₁  (Équation 1)

CEFDC Mesh 

À partir du point et Et suivre la signification du courant est une baisse potentielle R₂ (-), une autre tombe ET₂, Puisque le courant entre par le poteau de batterie + et enfin une autre tombe R₃ (-), en même temps le courant Toi₁ Il traverse R₃ Dans la direction opposée (+).

La deuxième équation, avec les signes indiqués, reste de cette manière:

- R₂ Toi₂ - ET₂ -R₃ Toi₂ +R₃ Toi₁= 0

R₃Toi₁ - (R₂ +R₃₎ Toi₂ = E₂  (Équation 2)

Notez qu'il y a deux équations avec les deux inconnues et₁ et moi₂.

Étape 3

Alors le système d'équations ainsi formé est résolu.

Exercices résolus

Pour commencer, il est important de prendre en compte ce qui suit:

-Les cravates ou les courants de maillage peuvent se voir attribuer une direction arbitraire.

-À chaque maillage essentiel - ou «fenêtre» - que le circuit doit se voir attribuer un courant.

Peut vous servir: processus isococ

-Les courants en filet sont appelés avec des majuscules pour les distinguer des courants qui circulent dans les branches, bien que dans certains cas, le courant qui circule à travers une branche puisse le même que celui du maillage.

- Exemple 1

Trouvez les courants qui circulent à travers chaque résistance dans le circuit de la figure 3, si les éléments ont les valeurs suivantes:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; ET₁ = 12 V; ET₂ = 18 V

Solution

En premier lieu, il est nécessaire d'attribuer les courants de maillage et₁ et moi₂ et prenez le système d'équations déduit dans la section précédente, puis remplacez les valeurs données dans l'instruction:

- (R₁+R₃) Yo₁ +R₃Toi₂ = -E₁  (Équation 1)

R₃Toi₁ - (R₂ +R₃₎ Toi₂ = E₂     (Équation 2)

-

-(20 + 30) Toi₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-cinquanteToi₁ + 10i₂ = -12

10i₁ - 40 I₂ = 18      

Comme il s'agit d'un système de 2 x 2 équations, il peut être facilement résolu par réduction, en multipliant par 5 la deuxième équation pour éliminer l'inconnu Toi₁:

-cinquanteToi₁ + 10 I₂ = -12

50i₁ - 200 I₂ = 90

-     

-190 I₂= 78

Toi₂ = - 78/180 a = - 0.41 A

Le courant est immédiatement effacé Toi₁ de l'une des équations originales:

Toi₁ = (18 + 40 I₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 A

Le signe négatif dans le courant Toi₂ signifie que le courant dans le 2 maillage circule contraire au dessin.

Les courants de chaque résistance sont les suivants:

Pour la résistance R₁ Le courant circule Toi₁ = 0.16 A dans le sens dessiné, par résistance R₂ Le courant circule Toi₂ = 0.41 A contrairement aux dessins et à la résistance R₃ circule Toi₃ = 0.16- (-0.41) a = 0.57 A vers le bas.

Solution système par la méthode de Cramer

D'une manière matricielle, le système peut être résolu comme suit:

Étape 1: Calculer Δ

 Important: Lorsque Δ = 0, le système n'a pas de solution, c'est un système incompatible.

Étape 2: Calculer Δ₁

La première colonne est remplacée par les termes indépendants du système d'équations, en maintenant l'ordre dans lequel le système a été initialement soulevé:

Étape 3: Calculer₁

Toi₁ = Δ₁/ Δ = 300/1900 = 0.16 A

Étape 4: Calculer Δ₂

 Étape 5: Calculer₂

Toi₂ = Δ₂/ Δ = -780/1900 = -0.41 A

- Exemple 2

Déterminez le courant et les tensions à travers chaque résistance dans le circuit suivant, au moyen de la méthode des courants de maillage:

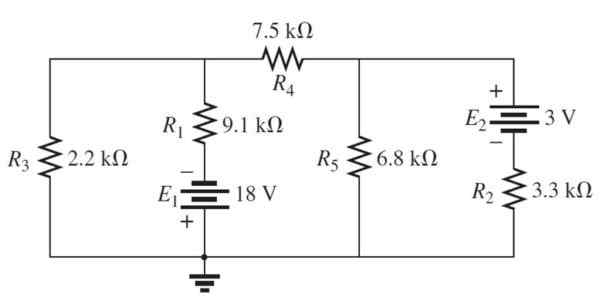Figure 4. Circuit de 3 mailles. Source: Boylestad, R. 2011. Introduction à l'analyse des circuits.2e. Édition. Pearson.

Solution

Les trois courants de maillage sont dessinés, comme le montre la figure suivante, dans des sens arbitraires. Maintenant, les mailles fonctionnent de n'importe où:

Il peut vous servir: Imantation: ce qui consiste, la méthode et les exemples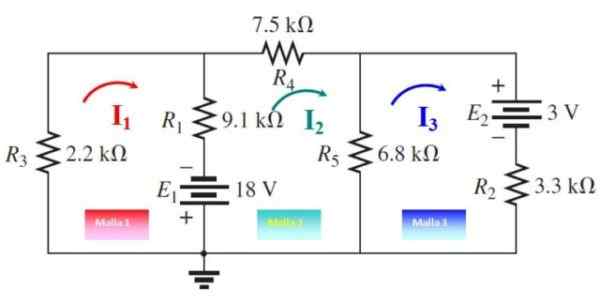 Figure 5. Courants de maillage pour l'exercice 2. Source: F. Zapata, modifié à partir de boylestad.

Maillage 1

-9100.Toi₁+18-2200.Toi₁+9100.Toi₂= 0

-11300 I₁ + 9100.Toi₂ = -18

Mesh 2       

-(7500 +6800 +9100) .Toi₂ + 9100.Toi₁+6800.Toi₃-18 = 0

9100.Toi₁ - 23400.Toi₂ + 6800.Toi₃ = 18

Mesh 3  

-(6800 + 3300) I₃ + 6800.Toi₂ - 3 = 0

6800.Toi₂ - 10100.Toi₃ = 3

Système d'équations

-11300 I₁ + 9100.Toi₂ + 0.Toi₃= -18

9100.Toi₁ - 23400.Toi₂ + 6800.Toi₃ = 18

0.Toi₁ + 6800.Toi₂ - 10100.Toi₃ = 3

Bien que les nombres soient grands, il est rapidement résolu à l'aide d'une calculatrice scientifique. N'oubliez pas que les équations doivent être commandées et ajouter des zéros aux endroits où l'inconnu n'apparaît pas, car il apparaît ici.

Les courants en filet sont:

Toi₁ = 0.0012 a; Toi₂ = -0.00048 a; Toi₃ = -0.00062 a

Les courants Toi₂ et Toi₃ Ils circulent dans la direction opposée sur la figure, car ils se sont avérés négatifs.

Tableau des courants et tensions dans chaque résistance

Résistance (ω)	Courant (ampères)	Tension = i.R (Volts)
9100	Toi1 -Toi2 = 0.0012 - (- 0.00048) = 0.00168	quinze.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Toi2 -Toi3= -0.00048 - (- 0.00062) = 0.00014	0.95

Solution de règles de Cramer

Puisqu'ils sont un grand nombre, il est pratique d'utiliser la notation scientifique pour travailler avec eux directement.

Calcul de i₁

Les flèches de couleur dans le déterminant 3 x 3 indiquent comment trouver des valeurs numériques, en multipliant les valeurs indiquées. Commençons par obtenir ceux du premier support dans le déterminant Δ:

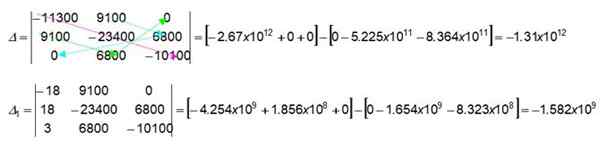
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Nous obtenons immédiatement le deuxième support dans ce même déterminant, qui fonctionne de gauche à droite (pour ce support, les flèches colorées n'ont pas été dessinées sur la figure). Nous invitons le lecteur à le vérifier:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^onze

6800 x 6800 x (-11300) = -5.225 x 10^onze

De la même manière, le lecteur peut également vérifier les valeurs du déterminant Δ₁.

Important: Entre les deux supports, il y a toujours un signe négatif.

Enfin, le courant est obtenu Toi₁ à travers Toi₁ = Δ₁ / Δ

Toi₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 A                                   

Calcul de i₂

La procédure peut être répétée pour calculer Toi₂, Dans ce cas, pour calculer le déterminant δ₂ La deuxième colonne du déterminant Δ est remplacée par la colonne des termes indépendants et sa valeur est trouvée, selon la procédure expliquée.

Cependant, comme c'est lourd en raison de grands nombres, surtout s'il n'y a pas de calculatrice scientifique, la plus simple est de remplacer la valeur de Toi₁ Déjà calculé, dans l'équation suivante et claire:

-11300 I₁ + 9100.Toi₂ + 0.Toi₃= -18 → 9100 I₂= -18 + 11300 I₁ → I₂ = -0.00048 a

Calcul i3

Une fois avec les valeurs de Toi₁ et Toi₂ En main, le Toi₃ Il est directement trouvé par substitution.

Les références

1. Alexander, C. 2006. Fondations du circuit électrique. 3e. Édition. Mc Graw Hill.
2. Boylestad, R. 2011. Introduction à l'analyse des circuits.2e. Édition. Pearson.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 5. Interaction électrique. Édité par Douglas Figueroa (USB).
4. Garcia, L. 2014. Électromagnétisme. 2e. Édition. Université industrielle de Santander.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume.