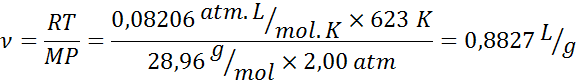Volume spécifique

Nous expliquons quel est le volume spécifique, sa formule, ses unités, comment elle est calculée et nous donnons plusieurs exemples de calcul

Quel est le volume spécifique?

Il Volume spécifique (Représenté avec le symbole ν, la lettre grecque Nu) est une propriété intensive de l'affaire qui mesure le volume occupé par unité de masse d'un corps. Correspond à la relation entre le volume et la masse, il représente donc l'inverse de la densité. Cela signifie que, plus le corps est dense, plus son volume spécifique et vice versa.

Connaître le volume spécifique d'une substance est important dans les applications dans lesquelles le volume disponible est limité. Par exemple, en sélectionnant le carburant pour une fusée spatiale, l'idéal est que le carburant a un volume possible, car sinon il prendra trop d'espace, ce qui nécessitera une fusée très grande et coûteuse.

Les volumes spécifiques sont également d'une grande importance dans le domaine de la thermodynamique, car ils permettent de calculer simplement les volumes molaires de différentes substances de sa masse molaire, ou de déterminer le volume total d'un échantillon de sa masse.

Enfin, des changements de volume spécifiques permettent également des changements de phase tels que la fusion et l'ébullition, entre autres.

Formule de volume spécifique

L'équation suivante correspond à la définition mathématique du volume spécifique:

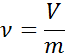
Où v est le volume d'un corps ou d'une substance, m est sa masse et ν est le volume spécifique. Cependant, il peut également être calculé à partir de la densité, car, comme mentionné ci-dessus, le volume spécifique est l'inverse de la densité:

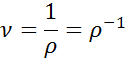
Où ρ représente la densité.

Unités de volume spécifiques

Les unités de volume spécifiques sont des unités de volume sur les unités de masse. Comme d'habitude, ces amplitudes peuvent être exprimées dans différents systèmes d'unités, de sorte que le volume spécifique peut également être exprimé en différentes unités.

Il peut vous servir: électrophile: réactions, exemples, électrophylité

Le tableau suivant montre les unités de volume spécifiques dans les systèmes d'unités les plus importantes:

Système d'unité	Unités de volume spécifiques
S.Toi.	M3 / kg
Mks	M3 / kg
CGS	cm3 / g
Système anglo-saxon	PIE3 / LB
Autres unités	ml / g ou cm3 / g

Calcul de volume spécifique

Pour les solides réguliers

Dans le cas de solides réguliers, le moyen le plus simple de déterminer le volume spécifique est de déterminer le volume des dimensions du solide, puis de diviser entre la masse.

Pour déterminer le volume du solide, la formule de volume correspondant à la forme particulière du solide (sphère, cône, cylindre, etc.).

Exemple 1: barre cylindrique

Vous avez une barre cylindrique solide de 2,54 cm d'épaisseur, 10 cm de long et une masse de 1,50 kg. Déterminer le volume spécifique du matériau en unités du s.Toi.

• Solution: Comme nous savons qu'il s'agit d'un cylindre, nous devons donc utiliser la formule de volume d'un cylindre, puis appliquer la formule de volume spécifique. Les deux équations peuvent être combinées en une comme indiqué ci-dessous:

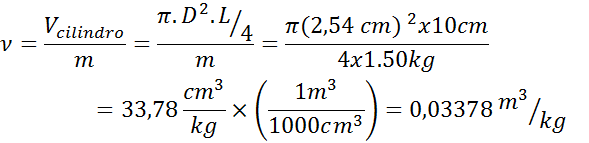
Exemple 2: sphère de verre

Un marbre en verre de 1 cm de diamètre est pesé dans un équilibre. Cela a lu 2,50 g. Déterminez le volume spécifique de verre.

• Solution: D'après le diamètre, on sait que le rayon de la sphère est de 0,50 cm. Avec ce rayon et en utilisant la formule de volume d'une sphère, nous pouvons déterminer le volume du marbre. Ensuite, nous utilisons la formule de volume spécifique. Vous pouvez également combiner les deux équations en une seule:

Peut vous servir: trioxyde d'arsenic (AS2O3)

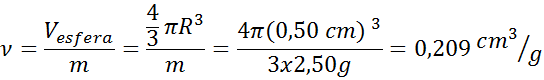
Pour les solides amorphes

Dans le cas de solides amorphes, il n'est pas possible de déterminer son volume au moyen de formules, car ce ne sont pas des solides réguliers. Une solution possible consiste à déterminer le volume du corps au moyen du volume qui déplace lors de l'immersion dans l'eau ou un autre liquide:

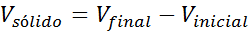
Exemple 3: une météorite

Une météorite a été trouvée très étrangement. Il a d'abord été pesé, après quoi une masse de 185,3 g a été obtenue. Ensuite, il a été introduit dans un cylindre gradué qui contenait 50,0 ml d'eau. Après avoir submergé la météorite, le niveau de l'eau est passé à 73,5 ml. Déterminer le volume spécifique de la météorite.

• Solution: Comme mentionné ci-dessus, le volume de la météorite est déterminé par le déplacement du liquide. La différence entre les volumes d'eau dans le cylindre gradué avant et après la publication de la météorite donne le volume du même. Ensuite, la formule de volume spécifique est appliquée:

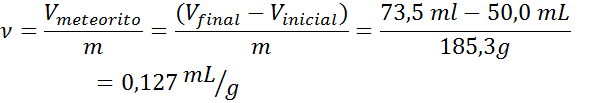
Exemple 4: un rocher

Près du site où la météorite de l'exemple précédent a été trouvée, un autre rocher a été trouvé avec une apparence similaire. Cela a également été pesé, obtenant une masse de 125 g et s'était immergé dans l'eau, où il a déplacé 15,90 ml du liquide. Déterminez s'il s'agit ou non d'un fragment de météorite.

• Solution: Le volume spécifique est une propriété intensive, donc si la roche est faite du même matériau que la météorite, elle devrait avoir le même volume spécifique.

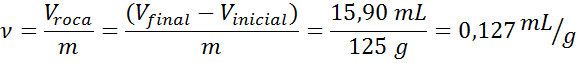
Comme on peut le voir, le volume spécifique de la roche est identique à celui de la météorite, il est donc possible que la roche soit un fragment de celui-ci.

Il peut vous servir: Nitrobenzène (C6H5N2): structure, propriétés, utilisations, risques

Liquide

Calculer le volume spécifique d'un liquide est effectué de la même manière qu'il a été montré dans les exemples précédents. Le volume peut être facilement mesuré à l'aide de matériau volumétrique. Vous pouvez également calculer le volume spécifique à partir de la densité du liquide, comme indiqué dans l'exemple suivant.

Exemple 5: volume spécifique d'alcool dénaturé

Déterminez le volume spécifique de l'alcool dénaturé, sachant qu'il a une densité de 0,876 g / ml.

• Solution: Nous savons que le volume spécifique est l'inverse de la densité, donc:

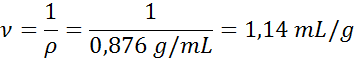
Pour les gaz

Compte tenu du fait que la plupart des gaz conformesnt à la loi idéale sur les gaz, alors cette équation peut être utilisée pour déterminer la valeur de volume spécifique d'un gaz. Après avoir réorganisé cette équation, la relation suivante est obtenue:

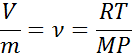
où r, t, m et p sont la constante des gaz idéaux, la température, la masse molaire de gaz et de pression, respectivement.

Exemple 6: Volume d'air spécifique

Calculez le volume spécifique d'un échantillon d'air trouvé à 2 atm de pression et 350 ° C, sachant que la masse molaire moyenne de l'air est de 28,96 g / mol.

• Solution: Pour utiliser cette équation, il est nécessaire de transformer la température en Kelvin en ajoutant 273 à la température en degrés Celsius: t = 350 + 273 = 623 K. Nous pouvons maintenant appliquer l'équation précédente, en utilisant la valeur de la constante r = 0,08206 ATL.L / mol.K: