Volume atomique

Qu'est-ce que le volume atomique?

Il Volume atomique C'est une valeur relative qui indique la relation entre la masse molaire d'un élément et sa densité. Ensuite, ce volume dépend de la densité de l'élément, et la densité dépend de la phase et de la façon dont les atomes sont ordonnés.

De sorte que le volume atomique pour un élément z n'est pas le même dans une autre phase différente de celle qu'elle présente à température ambiante (liquide, solide ou gaz), ou lorsqu'il fait partie de certains composés. Ainsi, le volume atomique de Z dans le composé ZB est différent du Z dans le composé ZB.

Parce que? Pour le comprendre, il est nécessaire de comparer les atomes avec, par exemple, des billes. Les billes ont leur bordure matérielle très bien définie, ce qui est observé grâce à leur brillante surface. D'un autre côté, la frontière des atomes est diffuse, bien qu'elles puissent être considérées comme sphériques à distance.

Ainsi, ce qui détermine un point au-delà de la bordure atomique, c'est la probabilité de vide de trouver un électron, et ce point peut être plus ou plus proche du noyau en fonction du nombre d'atomes voisins interagissent autour de l'atome en considération.

Volume atomique et radio

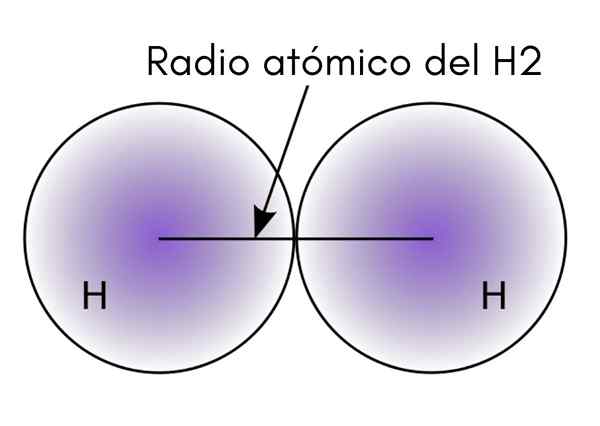
Lors de l'interaction de deux atomes H dans la molécule H₂, Les positions de leurs noyaux sont définies ainsi que les distances entre elles (distances internucléaires). Si les deux atomes sont sphériques, le rayon est la distance entre le noyau et la bordure diffuse:

Dans l'image supérieure, on peut voir comment la probabilité de trouver un électron diminue à mesure qu'elle s'éloigne du noyau. Divisant par deux la distance internucléaire, le rayon atomique est obtenu. Ensuite, en supposant une géométrie sphérique pour les atomes, la formule est utilisée pour calculer le volume d'une sphère:

V = (4/3) (pi) r³

Dans cette expression, R est le rayon atomique déterminé pour la molécule H₂. La valeur V calculée par cette petite méthode précise peut changer si, par exemple, H est considéré₂ à l'état liquide ou métallique. Cependant, cette méthode est très inexacte car les formes d'atomes sont très loin de la sphère idéale dans leurs interactions.

Pour déterminer les volumes atomiques dans les solides, de nombreuses variables concernant la disposition sont prises en compte et qui sont obtenues par des études de diffraction des rayons X.

Formule supplémentaire

La masse molaire exprime la quantité de matière qui a une mole d'atomes d'un élément chimique.

Ses unités sont g / mol. D'un autre côté, la densité est le volume qui occupe un gramme de l'élément: g / ml. Parce que les unités de volume atomique sont ML / MOL, vous devez jouer avec les variables pour atteindre les unités souhaitées:

• (g / mol) (ml / g) = ml / mol

Ou quel est le même:

• (Masse molaire) (1 / d) = V
• (Masse molaire / d) = V

Ainsi, le volume d'une mole d'atomes d'un élément peut facilement calculer; tandis qu'avec la formule du volume sphérique, le volume d'un atome individuel est calculé.

Pour atteindre cette valeur à partir du premier, une conversion est nécessaire à travers le numéro Avogadro (6,02 · 10^-23).

Comment varie le volume atomique dans le tableau périodique?

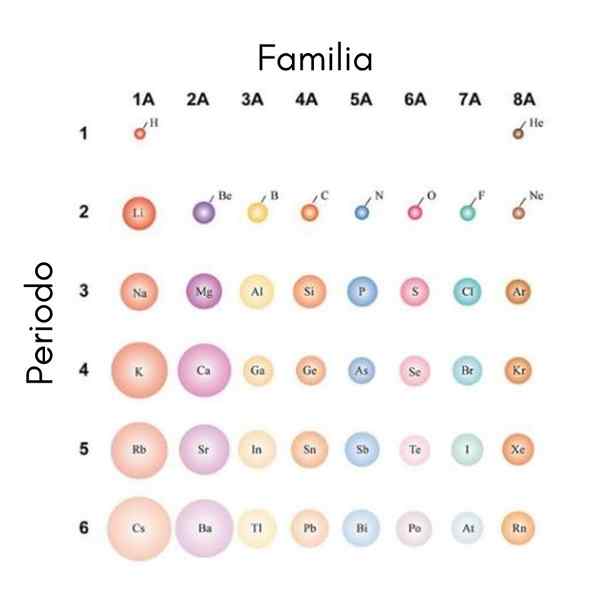
Si les atomes sont considérés comme sphériques, alors leur variation sera la même qui est observée dans les radios atomiques. Dans l'image supérieure, qui montre les éléments représentatifs, il est illustré que de droite à gauche les atomes nains; D'un autre côté, de haut en bas, ceux-ci deviennent plus volumineux.

En effet, dans la même période, le noyau intègre des protons lorsqu'il se déplace vers la droite. Ces protons exercent une force d'attraction sur les électrons externes, qui ressentent une charge nucléaire efficace z_Ef, mineur que vraie charge nucléaire z.

Les électrons des couches internes repoussent ceux de la couche externe, réduisant l'effet du noyau sur eux; Ceci est connu comme l'effet d'écran. Dans la même période, l'effet d'écran ne contrecarre pas l'augmentation du nombre de protons, de sorte que les électrons de la couche intérieure n'empêchent pas la contraction des atomes.

Cependant, lorsque vous descendant dans un groupe, de nouveaux niveaux d'énergie sont activés, ce qui permet aux électrons d'orbiter le noyau. De même, le nombre d'électrons dans la couche intérieure est augmenté, dont les effets de blindage commencent à diminuer si le noyau ajoute à nouveau des protons.

Pour ces raisons, il est apprécié que le groupe 1a ait les atomes les plus volumineux, contrairement aux petits atomes du groupe 8a (ou 18), celui des gaz nobles.

Volumes atomiques de métaux de transition

Les atomes des métaux de transition intègrent des électrons dans les orbitales internes d. Cette augmentation de l'effet d'écran et, ainsi que la véritable charge nucléaire Z, sont presque également annulées, de sorte que leurs atomes conservent une taille similaire au cours de la même période.

En d'autres termes: dans une période, les métaux de transition présentent des volumes atomiques similaires. Cependant, ces petites différences sont extrêmement significatives lors de la définition des cristaux métalliques (comme s'ils étaient des billes métalliques).

Exemples de volume atomique

Deux formules mathématiques sont disponibles pour calculer le volume atomique d'un élément, chacun avec ses exemples correspondants.

Exemple 1

Étant donné le radiogrogène atomique -37 PM (1 picomètre = 10^-12m) -et le césium -265 pm-, calculez vos volumes atomiques.

En utilisant la formule de volume sphérique, vous avez alors:

V_H= (4/3) (3.14) (15 h)³= 212,07 PM³

V_CS= (4/3) (3.14) (265 pm)³= 77912297.67 PM³

Cependant, ces volumes exprimés dans les picomètres sont exorbitants, ils se transforment donc en unités angstroms, les multipliant par le facteur de conversion (1Å / 100pm)³:

(212.07³) (1Å / 100pm)³= 21207 × 10^-4 POUR³

(77912297.67 PM³) (1Å / 100pm)³= 77 912 ų

Ainsi, les différences de taille entre le petit atome H et l'atome volumineux de CS sont en évidence numériquement. Il est nécessaire de prendre en compte que ces calculs ne sont rien de plus que des approximations dans l'affirmation selon laquelle un atome est totalement sphérique, qui divagate la réalité.

Exemple 2

La densité de l'or pur est de 19,32 g / ml et sa masse molaire est de 196,97 g / mol. En appliquant la formule M / D pour calculer le volume d'une mole d'atomes d'or, ce qui suit est:

V_Au= (196,97 g / mol) / (19,32 g / ml) = 10,19 ml / mol

C'est-à-dire que 1 mol d'atomes d'or occupe 10,19 ml, mais quel volume occupe spécifiquement un atome d'or? Et comment l'exprimer en unités PM³? Pour cela, appliquez simplement les facteurs de conversion suivants:

(10,19 ml / mol) · (mol / 6,02 · 10^-23 atomes) · (1 m / 100 cm)³· (13 h / 10^-12m)³= 16,92 · 10⁶ p.m³

D'un autre côté, le rayon atomique de l'or est 166 h. Si les deux volumes sont comparés - celui obtenu par la méthode précédente et qui est calculé avec la formule du volume sphérique - il sera constaté qu'ils n'ont pas la même valeur:

V_Au= (4/3) (3.14) (166 pm)³= 19,15 · 10⁶ p.m³

Lequel des deux est plus proche de la valeur acceptée? Celui qui est le plus proche des résultats expérimentaux obtenus par diffraction des rayons x de la structure cristalline de l'or.