Volume

Nous expliquons quel est le volume, ses formules, ses unités, comment la calculer et donner plusieurs exemples

Quel est le volume?

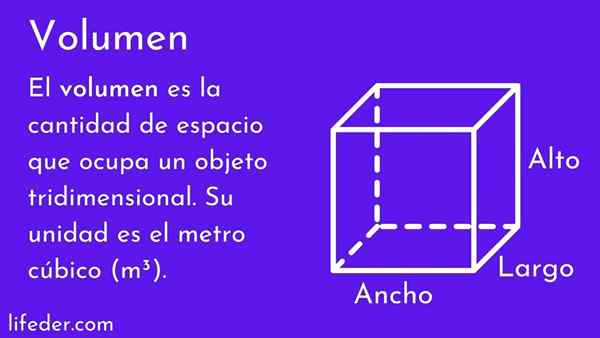
Il volume d'un corps est la valeur numérique qui mesure la quantité d'espace occupée par elle. Plus la largeur, la largeur et la profondeur déterminent le volume, plus, plus l'espace occupé est grand.

Le concept de volume est d'une grande importance, car le monde est trois dimensions et tous les objets ont une largeur, une hauteur et une profondeur, donc ils ont un volume. Les gens l'utilisent fréquemment, par exemple en estimant si les meubles qu'ils souhaitent acheter, il s'intègre dans leur chambre ou s'ils entrent dans une certaine taille de robe.

Dans certains domaines de la science et de l'ingénierie, comme lorsque vous travaillez avec des liquides, qu'il s'agisse de liquides ou de gaz, le volume occupé acquiert une grande importance: lors du remplissage des conteneurs et du pompage des fluides tels que de l'eau ou dans la conception d'un navire pour un navire pour vous assurer Tu ne coule pas. Tout cela rend essentiel à le déterminer pour de nombreux processus.

Il existe des formules pour calculer le volume de corps géométriques dans des formes régulières, telles que les prismes, les sphères, les cylindres et les cônes, par exemple, selon certaines de ses dimensions. Et il existe également des moyens de découvrir le volume d'objets irréguliers, comme vous le décrira un peu plus tard.

Formules de volume dans les figures géométriques

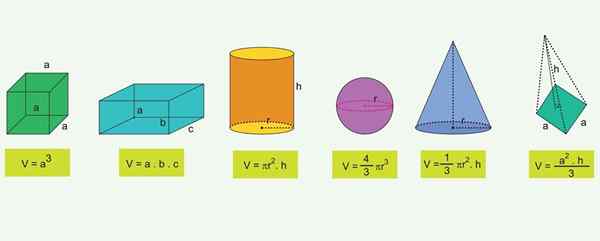
Liste des figures géométriques les plus courantes et la formule de leurs volumes

Pour les objets géométriques les plus connus, il existe des formules qui permettent de calculer son volume:

• cube

V = ℓ³ 

Où V représente le volume et ℓ est le bord (côté) du cube.

• Parallélépipède

Un parallélépipé est une boîte rectangulaire avec une largeur "A", une hauteur longue et "h". Son volume est donné par le produit de ses trois dimensions:

V = a ∙ ℓ ∙ h

• Sphère

Le volume de la sphère dépend de son rayon R:

Peut vous servir: Nicolás Copernico

• Cylindre circulaire droit

Le volume du cylindre circulaire droit est le produit entre la zone de sa base et sa hauteur "H". Comme la base est un album radio «R», dont la zone est a = π · r², Le volume demeure:

V = πr²∙ H

• Chatte

Le volume du cône est un tiers du produit entre la zone de la base circulaire A et la hauteur H. Comme a = πr², ensuite:

• Pyramide

Pour une pyramide dont la zone de base est A et a une hauteur «H», le volume est donné par:

Si la pyramide a une base carrée sur le côté "A", comme sur la figure, la zone de base de la base est de² Et le volume de la pyramide est:

V = (1/3) ⋅a²⋅H

• Prisme

Le volume du prisme est le produit entre la zone de la base A et la hauteur "H":

V = a ∙ h

Unités de volume

Dans le système international d'unités, l'unité de volume est le compteur cube ou M³, tandis que dans le système anglo-saxon, c'est le pied cube ou le ft³ (de Pieds, qui en anglais signifie "pied").

Il existe de nombreuses autres unités, selon la taille de l'espace occupé. Par exemple, kilomètres cubes km³ Pour des volumes plus grands ou des millimètres cubes mm³ Pour les petits volumes. Il existe également des unités d'utilisation locales.

Il est également nécessaire de mentionner les unités de capacité, étroitement liées à celles du volume, qui sont de préférence utilisées pour les liquides. L'unité de capacité centrale est le litre, l'abrégé L, qui équivaut à un DM³ (Décimètre cube).

Les autres unités qui méritent d'être mentionnées sont le gallon, le pouce cube, la tasse et la goutte, ce dernier utilisé pour dose des médicaments.

Peut vous servir: méthode comparative

Comment le volume est-il mesuré?

Le volume d'un corps, comme toute autre mesure, est réalisé en comparant avec un modèle adéquat, dans ce cas une unité de volume.

L'unité de volume est définie comme le cube dont le bord mesure 1 unité. Cette unité peut être un mètre, un centimètre, un pied, un pouce ou tout autre. Ensuite, le volume de l'objet correspond à la quantité d'unités cubes occupées par la figure et est toujours un montant positif.

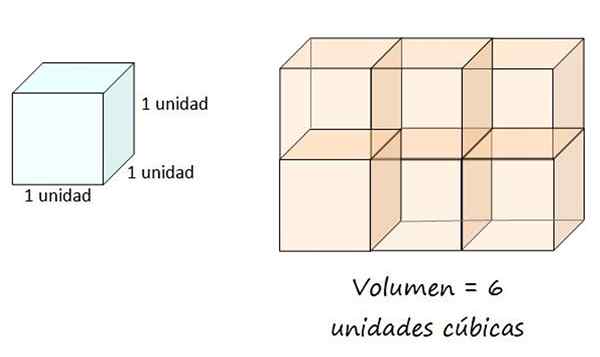Une unité cube est définie comme le volume d'un seau avec un bord égal à 1, donc la boîte à droite a un volume de 6 unités cubes. Source: F. Zapata.

Volume d'un corps géométrique

Lorsqu'il s'agit d'un corps géométrique comme déjà mentionné, le volume est calculé à travers la formule appropriée, mesurant les dimensions indiquées par la formule.

Par exemple, si vous voulez connaître le volume d'une sphère, il est nécessaire de mesurer son diamètre et avec elle son rayon est connu, qui est la moitié. S'il s'agit d'une boîte rectangulaire, la largeur, la hauteur et la profondeur de la même.

Ensuite, les valeurs demandées dans la formule sont insérées, en prenant soin que toutes les unités sont les mêmes, les opérations requises sont effectuées, il y a le volume de l'objet.

Volume d'un corps irrégulier

Les solides irréguliers n'ont pas de forme géométrique, comme une pierre ou un clin d'œil. Même ainsi, vous pouvez trouver son volume à l'aide d'un récipient gradué plein d'eau, au moyen de la méthode de déplacement liquide.

En premier lieu, le volume occupé par l'eau est déterminé puis l'objet irrégulier est complètement immergé, mesurant le nouveau volume, qui est supérieur à l'original. Le volume de l'objet irrégulier est la différence entre ce volume et celle de l'eau seule.

Peut vous servir: Genie Wiley, la fille sauvage qui n'a reconnu son nom que

Pour que cette méthode fonctionne, l'objet ne doit être fait d'une substance qui est facilement dissoute dans l'eau, elle doit rester complètement submergée et bien sûr, vous devez avoir un conteneur gradué de la taille nécessaire pour l'accueillir complètement.

Exemples de volume

Le volume approximatif de certains objets connus est:

• La terre: 1.08321 × 10¹² km³
• River Amazonas: 225.000 m³/ s (le volume par unité de temps est appelé "flux")
• La grande pyramide de Giza: 2.600.000 m³
• Un ballon de football: 5600 cm³
• Un sac à dos: 50 dm³

Volume et masse

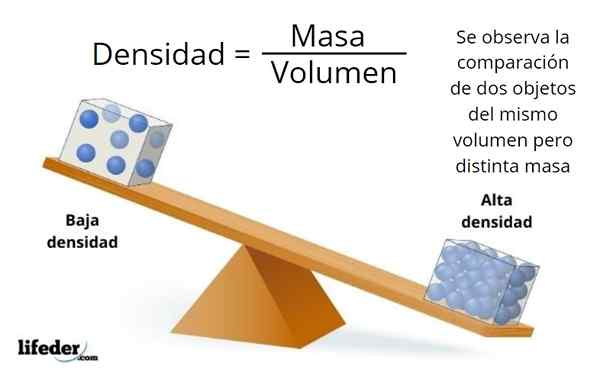
Le volume et la masse ne sont pas des synonymes, le premier est lié aux dimensions de l'objet et la seconde à la quantité de matière qu'il contient.

Il peut y avoir beaucoup de matière dans un objet de petites dimensions, ou très peu dans un grand objet, qui dépend de la densité du matériau, qui est le rapport entre la masse et le volume d'un objet:

Exercices résolus

Exercice 1

Calculez le volume d'une boîte rectangulaire dont les dimensions sont de 34 cm × 22 cm × 8 cm.

• Solution

Le volume d'une boîte rectangulaire est simplement le produit de ses trois dimensions:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Exercice 2

La base d'une pyramide quadrangulaire a une superficie de 16 cm² Et sa hauteur est de 6 cm. Calculez le volume de ladite pyramide.

• Solution

La formule donnée ci-dessus pour le volume d'une pyramide est utilisée, connu la zone de sa base:

Et les valeurs numériques sont remplacées:

V = (1/3) × 16 cm² × 6 cm = 32 cm³