Formules de vitesse moyennes, comment il est calculé et résolu l'exercice

La vitesse moyenne Pour une particule mobile, il est défini comme la raison entre la variation de la position qu'elle connaît et l'intervalle de temps utilisé dans le changement. La situation la plus simple est celle dans laquelle la particule se déplace le long d'une ligne droite représentée par l'axe x.

Supposons que l'objet mobile occupe les positions X₁ et x₂ Dans les temps t₁ et T₂ respectivement. La définition de la vitesse moyenne V_m Il est représenté mathématiquement comme suit:

Les unités de V_m Dans le système international, ils sont des compteurs / seconde (m / s). D'autres unités d'utilisation courantes qui apparaissent dans les textes et appareils mobiles sont les suivants: km / h, cm / s, miles / h, pieds / s et plus, à condition qu'ils soient la longueur / la forme du temps.

La lettre grecque "δ" lit "Delta" et est utilisée pour résumer la différence entre deux quantités.

[TOC]

Caractéristiques du vecteur de vitesse moyen V_m

La vitesse moyenne est une caractéristique importante du mouvement. Source: Pixabay

La vitesse moyenne est un vecteur, car il est lié au changement de position, qui à son tour est connu sous le nom Déplacement vectoriel.

Cette qualité est représentée en gras ou par une flèche sur la lettre qui désigne l'ampleur. Cependant, dans une dimension, la seule direction possible est celle de l'axe x et peut donc être distribuée avec la notation vectorielle.

Puisque les vecteurs ont l'ampleur, la direction et le sens, un regard initial sur l'équation indique que la vitesse moyenne aura la même direction et le même sens que le déplacement.

Imaginez la particule de l'exemple se déplaçant le long d'une ligne droite. Pour décrire votre mouvement, il est nécessaire d'indiquer un point de référence, qui sera «l'origine» et sera indiqué comme ou.

La particule peut s'éloigner ou s'approcher ou, soit à gauche, soit à droite. Vous pouvez également utiliser beaucoup ou peu de temps pour atteindre une certaine position.

Il peut vous servir: chaleur: formules et unités, caractéristiques, comment elle est mesurée, exemples

Les amplitudes qui ont été mentionnées: position, déplacement, intervalle de temps et vitesse moyenne, décrivent le comportement de la particule tout en se déplaçant. C'est une question de grandeur Cinématique.

Pour distinguer les positions ou les emplacements à gauche du signe ou le signe (-) est utilisé et ceux trouvés à droite ou portent le signe (+).

La vitesse moyenne a une interprétation géométrique qui peut être observée dans la figure suivante. C'est la pente de la ligne qui passe par les points P et Q. Lors de la coupe à la position vs position. Il est temps à deux points, c'est une ligne séchage.

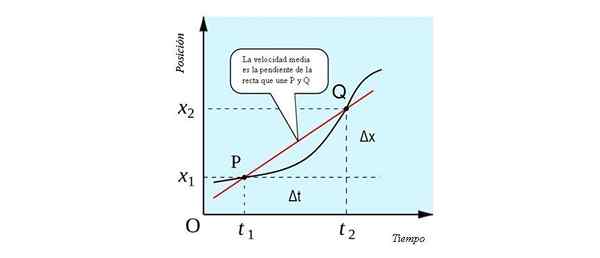Interprétation géométrique de la vitesse moyenne, comme une pente de la ligne qui rejoint les points P et Q. Source: すじにく シチュー [CC0].

Les signes de vitesse moyenne

Pour l'analyse suivante, il faut tenir compte que t₂ > t₁. C'est-à-dire que le moment suivant est toujours supérieur au courant. De cette manière t₂ - t₁ C'est toujours positif, ce qui a généralement du sens quotidien.

Alors le signe de la vitesse moyenne sera déterminé par le X₂ - X₁. Notez que c'est important.

Ou "avant" ou "dos", comme le lecteur préfère.

Si la vitesse moyenne est positive, cela signifie que En moyenne la valeur de "X«Augmente avec le temps, bien que cela ne signifie pas que cela aurait pu diminuer à un moment donné dans le temps considéré - Δt -.

Cependant en termes mondiaux, en fin de temps Δt, Elle s'est terminée avec une position plus grande que celle qu'elle avait au début. Les détails du mouvement sont ignorés dans cette analyse.

Vous pouvez vous servir: la troisième loi de Newton: applications, expériences et exercices

Et si la vitesse moyenne est négative? Eh bien, cela signifie que la particule se termine par une coordonnée plus petite que celle avec laquelle il a commencé. Le mode Groso a reculé. Regardons quelques exemples numériques:

Exemple 1: Compte tenu des positions initiales et finales indiquées, indiquez le signe de la vitesse moyenne. Où la particule a-t-elle bougé à l'échelle mondiale?

a) x₁ = 3 m; X₂ = 8 m

Répondre: X₂- X₁  = 8 m - 3 m = 5 m. Vitesse moyenne positive, la particule a avancé.

b) x₁ = 2 m; X₂ = -3 m

Répondre: X₂ - X₁ = -3 m -2 m = -5 m. Vitesse négative moyenne, la particule est reculé.

 c) x₁  = - 5 m; X₂ = -12 m

Répondre: X₂ - X₁   = -12 m - (- 5 m) = -7 m. Vitesse négative moyenne, la particule est reculé.

d) x₁  = - 4 m; X₂ = 10 m

Répondre: X₂ - X₁  = 10 m - (-4m) = 14 m. Vitesse moyenne positive, la particule a avancé.

La vitesse moyenne peut-elle être 0? Ouais. Tant que le point de départ et le point d'arrivée sont les mêmes. Est-ce à dire que la particule était nécessairement au repos tout le temps?

Non, cela signifie seulement que le voyage était aller-retour. Peut-être qu'il a voyagé rapidement ou peut-être très lentement. Pour l'instant il n'est pas connu.

La vitesse moyenne: une ampleur scalaire

Cela nous amène à définir un nouveau terme: le Vitesse moyenne. En physique, il est important de distinguer les amplitudes vectorielles et les amplitudes qui ne sont pas: les scalaires.

Pour la particule qui a fait l'aller-retour, la vitesse moyenne est de 0, mais elle aurait pu être très rapide ou peut-être pas. Pour le savoir, la vitesse moyenne est définie comme:

Les unités de la vitesse moyenne sont les mêmes que celles de la vitesse moyenne. La différence fondamentale entre les deux amplitudes est que la vitesse moyenne comprend des informations intéressantes sur la direction et la direction de la particule.

Il peut vous servir: condensat fermionique: propriétés, applications et exemples

D'un autre côté, la vitesse moyenne ne fournit que des informations numériques. Avec elle, on sait à quelle vitesse ou à ralentir la particule se déplaçait, mais pas s'il le faisait en avant ou en arrière. C'est pourquoi c'est une ampleur scalaire. Comment les distinguer pour les désigner? Une façon est de laisser audacieuse les vecteurs, ou de placer une flèche sur eux.

Et il est important de noter que la vitesse moyenne ne doit pas être égale à la vitesse moyenne. Pour l'aller-retour, la vitesse moyenne est nulle, mais la vitesse moyenne ne fait pas. Les deux ont la même valeur numérique lorsqu'ils voyagent toujours dans la même direction.

Exercice résolu

Vous rentrez chez vous de l'école tranquillement à 95 km / h par 130 km. Commencez à pleuvoir et réduit la vitesse à 65 km / h. Il rentre enfin à la maison après avoir conduit pendant 3 heures et 20 minutes.

a) Jusqu'où est la maison de votre école?

b) Quelle était la vitesse moyenne?

Réponses:

a) Certains calculs précédents sont nécessaires:

Le voyage est divisé en deux parties, la distance totale est:

D = d1 + d₂, Avec d1 = 130 km

Le temps total est de 3 heures et 20 minutes = 3 + 1/3 heures = 10/3 heures = 3.33 h (il est nécessaire de placer les mêmes unités pour le temps, dans ce cas, il est approprié).

T2 = 3.33 - 1.37 heures = 1.96 heures

Calcul de D_2:

d₂ = 65 km / h x 1.96 H = 125. 4 km.

L'école est d1 + d₂ = 255.4 km de la maison.

b) Vous pouvez maintenant trouver la vitesse moyenne:

Les références

1. Giancoli, D. La physique. Principes avec les applications. Sixième édition. Prentice Hall. 21-22.
2. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 20-21.
3. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7mame. Édition. Mexique. Cengage Learning Editors. 21-23.