Définition de vitesse instantanée, formule, calcul et exercices

La Vitesse instantanée Il est défini comme le changement instantané de déplacement dans le temps. C'est un concept qui ajoute une grande précision à l'étude du mouvement. Et c'est une avance en ce qui concerne la vitesse moyenne, dont les informations sont très générales.

Pour obtenir une vitesse instantanée, regardons un intervalle de temps aussi petit que possible. Le calcul différentiel est l'outil parfait pour exprimer cette idée mathématiquement.

La vitesse instantanée explique la vitesse mobile à chaque point de son itinéraire. Source: Pixabay.

Le point de départ est la vitesse moyenne:

Maintenant, faisons une approche Δt à 0 tout ce qui peut. C'est une limite et le résultat sera précisément la vitesse instantanée:

Cette limite est connue du nom de dérivé. Dans la notation du calcul différentiel, vous avez:

À condition que le mouvement soit limité à une ligne droite, il peut être distribué avec la notation vectorielle.

[TOC]

Calcul de vitesse instantanée: interprétation géométrique

La figure suivante montre l'interprétation géométrique du concept de dérivé: c'est la pente de la ligne tangente À la courbe x (t) vs. t À chaque point.

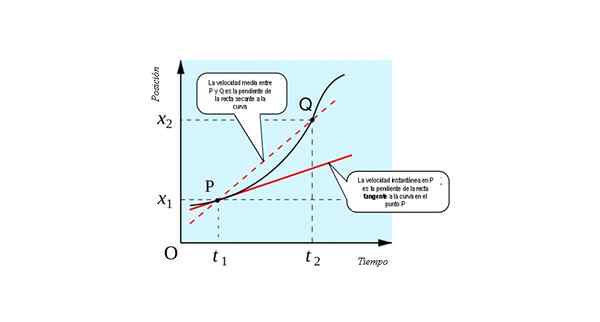La vitesse instantanée en p équivalent numériquement à la pente de la ligne tangente à la courbe x Vs. t au point p. Source: Source: すじにく シチュー [CC0].

Vous pouvez imaginer comment obtenir la limite si le point Q s'approche progressivement. Il arrivera un moment où les deux points seront si proches, que l'on ne peut pas être distingué de l'autre.

La ligne qui les unit alors sécher (droit qui coupe en deux points) pour être tangente (droite qui touche la courbe en un seul point). Par conséquent, pour trouver la vitesse instantanée d'une particule mobile, nous devrions avoir:

• Le graphique de la position de la particule en fonction du temps. Trouver la pente de la ligne tangente à la courbe à chaque moment du temps, vous avez la vitesse instantanée à chaque point occupé par la particule.

Peut vous servir: Ampère Loi: formule et équations, démonstration, exercices

Ou bien:

• La fonction de position des particules x (t), qui est dérivé pour obtenir la fonction de vitesse V (t), alors cette fonction est évaluée à chaque fois t, Une commodité. La fonction de position est censée être dérivable.

Quelques cas particuliers dans le calcul de la vitesse instantanée

-La pente de la ligne tangente à la courbe en p est 0. Une pente nul signifie que le mobile est arrêté et que sa vitesse bien sûr est 0.

-La pente de la ligne tangente à la courbe en p est supérieure à 0. La vitesse est positive. Dans le graphique ci-dessus, cela signifie que le mobile s'éloigne de ou.

-La pente de la ligne tangente à la courbe en p est inférieure à 0. La vitesse serait négative. Dans le graphique ci-dessus, il n'y a pas de points comme ça, mais dans ce cas, la particule approcherait ou.

-La pente de la ligne tangente à la courbe est constante en p et tous les autres points. Dans ce cas, le graphique est une ligne droite et le mobile a mouvement de ligne uniforme Mru (sa vitesse est constante).

En général, la fonction V (t) C'est aussi une fonction temporelle, qui à son tour peut avoir dérivé. Et s'il n'était pas possible de trouver ceux dérivés des fonctions x (t) et V (t)?

Dans le cas d x (t) Il se pourrait que la pente - la vitesse instantanée - ait changé de signe fortement. Ou qui passera de zéro à une valeur différente immédiatement.

Si c'est le cas les graphiques x (t) Il présenterait des conseils ou des coins aux changements soudains. Très différent du cas représenté dans l'image précédente, dans laquelle la courbe x (t) C'est une courbe douce, sans points, coins, discontinuités ou changements brusques.

Peut vous servir: Bose Einstein Condolaire

La vérité est que pour les vrais mobiles, les courbes douces sont celles qui représentent le mieux le comportement de l'objet.

Le mouvement général est assez complexe. Le mobile peut être arrêté pendant un certain temps, accélérez pour se déplacer du repos pour avoir une vitesse et s'éloigner du point de départ, garder la vitesse pendant un certain temps, puis s'arrêter pour s'arrêter et donc le style.

Ils peuvent recommencer et continuer dans la même direction. Ou agir le revers et le retour. C'est ce qu'on appelle un mouvement varié dans une dimension.

Ci-dessous, quelques exemples du calcul de la vitesse instantanée clarifieront l'utilisation des définitions données:

Exercices de vitesse instantanée résolus

Exercice 1

Une particule se déplace le long d'une ligne droite avec la loi de mouvement suivante:

x (t) = -t³ + 2 T² + 6 T - 10

Toutes les unités sont dans le système international. Trouver:

a) La position de la particule à t = 3 secondes.

b) La vitesse moyenne dans l'intervalle entre t = 0 s et t = 3 s.

c) La vitesse moyenne dans l'intervalle entre t = 0 s et t = 3 s.

d) La vitesse instantanée de la particule de la question précédente, à t = 1 s.

Réponses

a) Pour trouver la position de la particule, la loi de mouvement (fonction de position) à t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Il n'y a aucun problème que la position est négative. Le signe (-) indique que la particule est à gauche de l'origine ou.

b) Dans le calcul de la vitesse moyenne, les positions finales et initiales de la particule sont nécessaires dans les temps indiqués: x (3) et x (0). La position à t = 3 est x (3) et est connue du résultat précédent. La position à t = 0 secondes est x (0) = -10 m.

Peut vous servir: statique: histoire, quelles études, applications, lois

Comme la position finale est la même que celle initiale, il est immédiatement conclu que la vitesse moyenne est 0.

c) La vitesse moyenne est la raison entre la distance parcourue et le temps passé. Maintenant, la distance est le module ou l'ampleur du déplacement, donc:

Distance = | x2 - x1 | = | -10 - (- 10) | M = 20 m

Notez que la distance parcourue est toujours positive.

V_{m = 20 m / 3 s = 6.7 m / s}

d) Ici, il est nécessaire de trouver le premier dérivé de la position concernant le temps. Ensuite, il est évalué pour t = 1 seconde.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m / s = 6 m / s

Exercice 2

Vous trouverez ci-dessous le graphique de la position d'un mobile en fonction du temps. Trouvez la vitesse instantanée à t = 2 secondes.

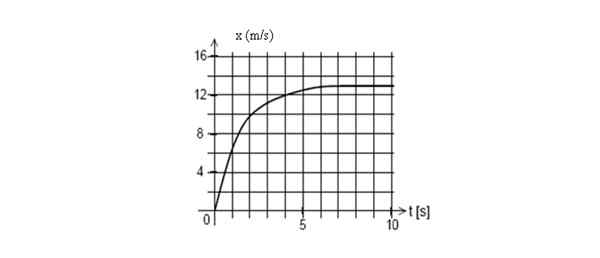Poster le graphique contre le temps pour un mobile. Source: auto-faite.

Répondre

Dessinez la ligne tangente sur la courbe à t = 2 secondes, puis calculez votre pente, en prenant deux points de la ligne.

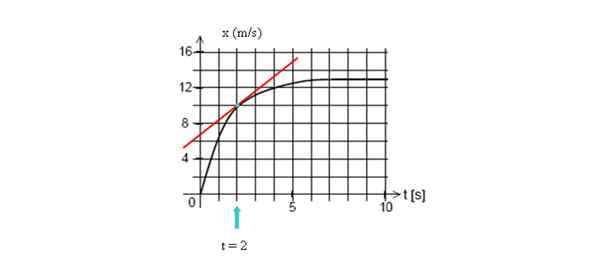Pour calculer la vitesse instantanée au point indiqué, tracez la ligne tangente à ce point et trouvez sa pente. Source: auto-faite.

Dans cet exemple, nous prendrons deux points facilement visualisés, dont les coordonnées sont (2 s, 10 m) et la coupe avec l'axe vertical (0 s, 7 m):

Les références

1. Giancoli, D. La physique. Principes avec les applications. 6^e Édition. Prentice Hall. 22-25.
2. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 21-22.
3. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7^mame. Édition. Mexique. Cengage Learning Editors. 23-25.