Vecteurs colinéaires

Nous expliquons ce que sont les vecteurs colinéaires, le système de vecteurs colinéaires et nous avons mis plusieurs exemples

Quels sont les vecteurs collinéaux?

Les Vecteurs colinéaires Ils sont l'un des trois types de vecteurs existants. Ce sont ces vecteurs qui sont dans le même sens ou la même ligne d'action. Cela signifie ce qui suit: deux vecteurs ou plus seront colinéaires s'il y a le cas où ils sont disposés en lignes parallèles les unes aux autres.

Un vecteur est défini comme une ampleur appliquée à un corps et se caractérise par une direction, un sens et une échelle. Les vecteurs peuvent être trouvés dans le plan ou dans l'espace et peuvent être de différents types: vecteurs colinéaires, vecteurs simultanés et vecteurs parallèles.

Quand y a-t-il des vecteurs colinéaux?

Les vecteurs sont colinéaires si la ligne d'action d'une est exactement la même ligne d'action de tous les autres vecteurs, quelle que soit la taille et la direction de chacun des vecteurs.

Les vecteurs sont utilisés comme représentations dans différents domaines tels que les mathématiques, la physique, l'algèbre et aussi en géométrie, où les vecteurs ne sont colinéaires que lorsque leur direction est la même, quelle que soit leur signification n'est pas.

Exemples de vecteurs colinéaires

• Deux vecteurs ou plus sont colinéaires si la relation entre les coordonnées est la même.

Exemple 1

Vous avez des vecteurs m = m_x; m_y et n = n_x; N_. Ce sont colinéaires si:

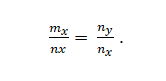
Exemple 2

Il peut être déterminé si les vecteurs j = 3,6,15 et p = 1,2,5 sont colinéaires à travers la relation de leurs coordonnées, que vous devez être proportionnelle les uns aux autres; c'est-à-dire: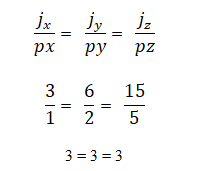

• Deux vecteurs ou plus sont colinéaires si la multiplication du produit ou des vecteurs est égale à zéro (0). En effet, dans le système de coordonnées, chaque vecteur est caractérisé par leurs coordonnées respectives, et si elles sont proportionnelles les unes aux autres, les vecteurs seront colinéaires. Ceci est exprimé comme suit:

Peut vous servir: ensembles équivalents: quelles sont, explication, exemples

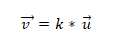
Exemple 1

Vous avez des vecteurs a = (10, 5) et b = (6, 3). Pour déterminer s'ils sont colinéaires, la théorie déterminante est appliquée, ce qui établit l'égalité des produits croisés. De cette façon, vous devez:

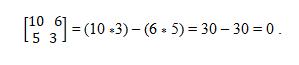
Système vectoriel colinéaire

Les vecteurs colinéaux sont représentés graphiquement en utilisant la direction et la direction de ceux-ci - ayant à l'esprit qu'il doit passer par le point d'application - et le module, qui est une échelle ou une longueur spécifique.

Le système vectoriel colinéaire est formé lorsque deux vecteurs ou plus agissent sur un objet ou un corps, qui représentent une force et agissent dans la même direction.

Par exemple, si deux forces colinéaires sont appliquées sur un corps, celles résultant ne dépendront que du sens dans lequel ils agissent. Il y a trois cas, qui sont:

Vecteurs colinéaires avec des sens opposés

Le résultat de deux vecteurs colinéaires est égal à la somme de ceux-ci:

R = ∑ f = f₁ + F_2.

Exemple

Si deux forces F agissent sur un chariot₁ = 40 N et F₂ = 20 N Dans la direction opposée (comme indiqué dans l'image), le résultat est:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

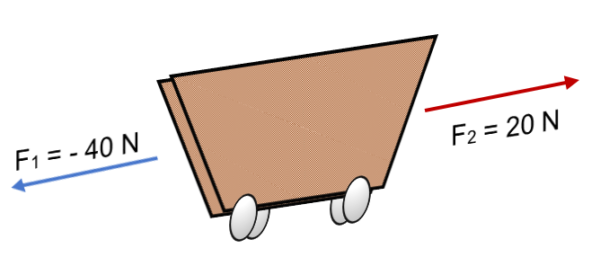Le signe négatif exprime que le corps se déplacera vers la gauche, avec une force équivalente à 20 N.

Vecteurs colinéaires dans le même sens

L'amplitude de la force résultante sera égale à la somme des vecteurs colinéaires:

R = ∑ f = f₁ + F_2.

Exemple

Si deux forces F agissent sur un chariot₁ = 35 n et f₂ = 55 N dans la même direction (comme indiqué dans l'image), le résultat est:

R = ∑ f = 35 n + 55n.

R = 90 n.

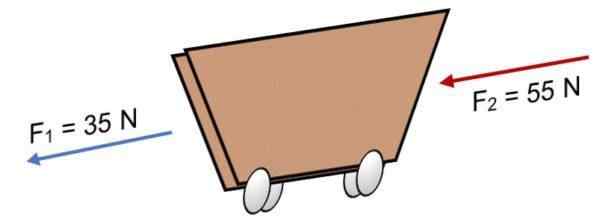
Le résultat positif indique que les vecteurs collinéaux agissent vers la gauche.

Il peut vous servir: règle t: caractéristiques, afin que ce soit, des exemples

Vecteurs colinéaires avec des amplitudes égales et des sens opposés

Le résultat des deux vecteurs colinéaux sera égal à la somme des vecteurs colinéaires:

R = ∑ f = f₁ + F_2.

Comme les forces ont la même ampleur mais dans la direction opposée - c'est-à-dire que l'on sera positif et un autre négatif -, en ajoutant les deux forces, le résultat sera égal à zéro.

Exemple

Si deux forces F agissent sur un chariot₁ = -7 n et f₂ = 7 n, qui ont la même ampleur, mais dans la direction opposée (comme indiqué dans l'image), le résultat est:

R = ∑ f = (-7 n) + 7n.

R = 0.

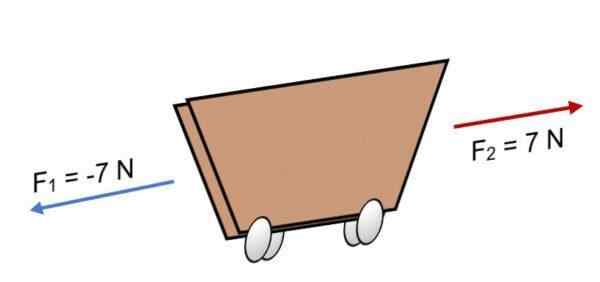
Comme le résultat est égal à 0, cela signifie que les vecteurs s'équilibrent entre eux et, par conséquent, le corps est en équilibre ou en repos (il ne bougera pas).

Différence entre les vecteurs colinéaires et simultanés

Les vecteurs colinéaires sont caractérisés par la même direction sur la même ligne, ou parce qu'ils sont parallèles à une ligne; C'est-à-dire que ce sont des vecteurs de directeurs parallèles.

De leur côté, les vecteurs simultanés sont définis car ils sont dans des lignes d'action différentes qui sont interceptées en un seul point.

En d'autres termes, ils ont le même point d'origine ou d'arrivée - Impossible de leur module, signification ou direction - formant un angle entre eux.

Les systèmes vectoriels simultanés sont résolus par des méthodes mathématiques ou graphiques, qui sont la méthode de parallélogramme des forces et la méthode du polygone des forces. Grâce à ceux-ci, la valeur d'un vecteur résultant sera déterminée, ce qui indique la direction dans laquelle un corps se déplacera.

Fondamentalement, la principale différence entre les vecteurs colinéaires et simultanés est la ligne d'action dans laquelle ils agissent: les colinéaux agissent dans la même ligne, tandis que les simultanément en différents.

Peut vous servir: système d'équations: méthodes de solution, exemples, exercices

C'est-à-dire que les vecteurs colinéaires agissent dans un seul plan, "x" ou "y"; Et l'acte simultané dans les deux plans, à partir du même point.

Les vecteurs colinéaires ne sont pas à un moment donné, comme le font les simultanément, car ils sont parallèles.

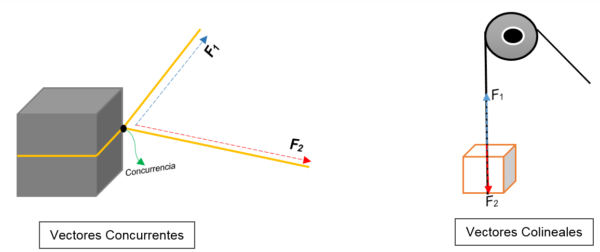
Dans l'image de gauche, vous pouvez voir un bloc. Il est attaché avec une corde et le nœud le divise en deux; Lorsqu'il est trouvé vers différentes orientations et avec différentes forces, le bloc se déplacera vers la même direction.

Deux vecteurs sont représentés à un moment donné (le bloc), quel que soit leur module, leur direction ou leur direction.

D'un autre côté, dans l'image droite, une poulie apparaît qui soulève une boîte. La corde représente la ligne d'action; Lorsqu'il est interrompu, deux forces (vecteurs) agissent dessus: une force de tension (lors de l'escalade du bloc) et une autre force, qui exerce le poids du bloc. Les deux ont la même direction, mais dans les sens opposés; Ils ne sont pas d'accord à un moment donné.