Caractéristiques et propriétés vectorielles, éléments, types, exemples

Les vecteurs Ce sont des entités mathématiques qui ont une ampleur positive -, généralement accompagnée d'une unité de mesure, en plus de la direction et du sens. Ces caractéristiques sont très appropriées pour décrire des quantités physiques telles que la vitesse, la force, l'accélération et bien d'autres.

Avec les vecteurs, il est possible d'effectuer des opérations telles que la somme, la soustraction et les produits. La division n'est pas définie pour les vecteurs et pour le produit, il y a trois classes que nous décrirons plus tard: produit scalaire ou point, vecteur ou produit transversal et produit d'un scalaire pour un vecteur.

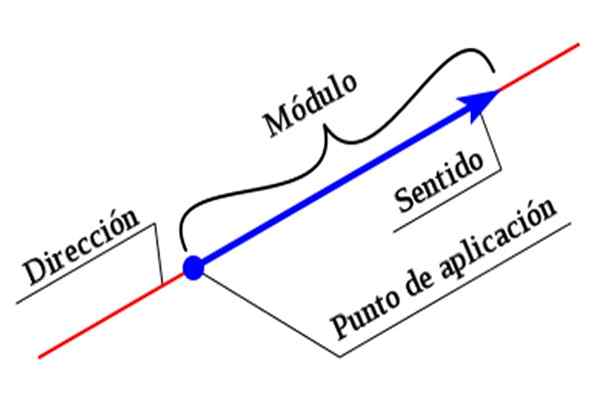Figure 1. Les éléments d'un vecteur. Source: Wikimedia Commons.

Pour décrire complètement un vecteur, il est nécessaire d'indiquer toutes ses caractéristiques. La magnitude ou le module est une valeur numérique accompagnée d'une unité, tandis que la direction et le sens sont établis à l'aide d'un système de coordonnées.

Regardons un exemple: Supposons qu'un avion vole d'une ville à l'autre à un rythme de 850 km / h dans la direction. Ici, nous avons un vecteur complètement spécifié, car l'ampleur est disponible: 850 km / h, tandis que la direction et le sens sont NE.

Les vecteurs sont généralement représentés graphiquement par des segments de ligne orientés, dont la longueur est proportionnelle à l'ampleur.

Alors que pour spécifier la direction et la signification, une ligne de référence est requise qui est généralement l'axe horizontal, bien que le nord puisse également être considéré comme une référence, tel est le cas de la vitesse du plan:

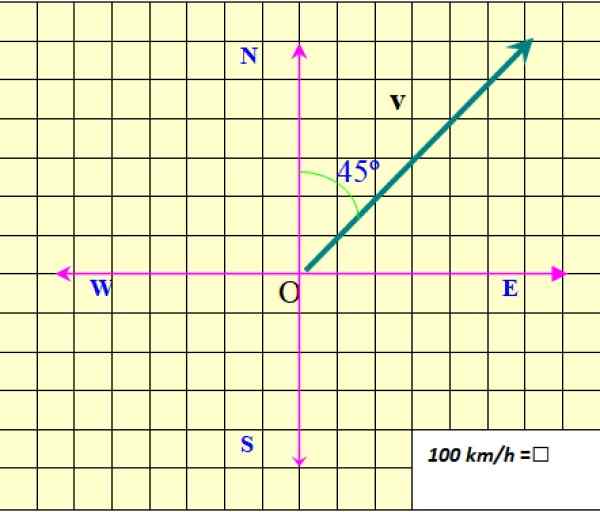Figure 2. Un vecteur de vitesse. Source: F. Zapata.

La figure montre le vecteur de vitesse du plan, qui est indiqué comme V dans gras, pour le distinguer d'une quantité scalaire, qui ne nécessite qu'une valeur numérique et une unité à spécifier.

[TOC]

Éléments d'un vecteur

Comme nous l'avons dit, les éléments vectoriels sont:

-Magnitude ou module, parfois aussi appelé valeur absolue ou norme vectorielle.

-adresse

-Sens

Dans l'exemple de la figure 2, le module de V C'est 850 km / h. Le module est indiqué comme V sans gras, ou comme |V|, Où les barres représentent la valeur absolue.

L'adresse de V est spécifié par rapport au nord. Dans ce cas, il est à 45 ° au nord de l'est (45 ° NE). Enfin, la pointe de la flèche informe sur la direction de V.

Dans cet exemple, l'origine vectorielle a été dessinée en coïncidant avec le système d'origine ou de coordonnées, c'est ce qu'on appelle Vecteur lié. D'un autre côté, si l'origine du vecteur ne correspond pas à celle du système de référence, il est dit que c'est un vecteur libre.

Il convient de noter que pour spécifier complètement le vecteur, ces trois éléments doivent être indiqués, sinon la description du vecteur serait incomplète.

Composants rectangulaires d'un vecteur

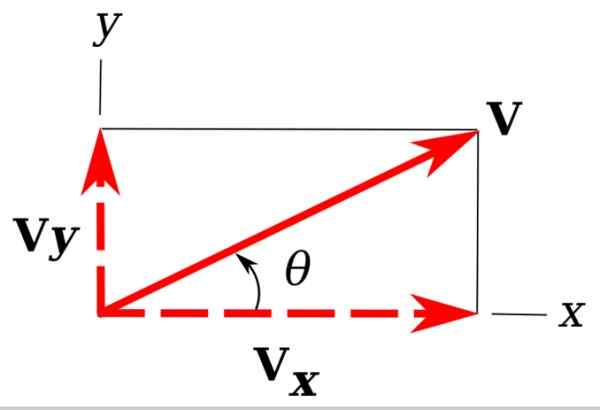figure 3. Composants rectangulaires d'un vecteur dans le plan. Source: Wikimedia Commons. Unther [cc by-sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Dans l'image, nous avons le retour de notre exemple de vecteur V, c'est dans l'avion Xy.

Il est facile de remarquer que les projections V sur les axes de coordonnées x et y déterminent un triangle droit. Ces projections sont V_et et V_X et sont appelés composants rectangulaires de V.

Un moyen de désigner V À travers ses composants rectangulaires, c'est comme ceci: V = X, V_et>. Ces crochets sont utilisés à la place des parenthèses pour souligner le fait qu'il s'agit d'un vecteur et non d'un point, car dans ce cas, des parenthèses seraient utilisées.

Peut vous servir: James Chadwick: biographie, modèle atomique, expériences

Si le vecteur est dans l'espace à trois dimensions, un autre composant est nécessaire, de sorte que:

V = X, V_et, V_z>

Connaissant les composants rectangulaires, l'ampleur du vecteur est calculée, équivalente à trouver l'hypoténuse du triangle droit dont les jambes sont V_X et V_et,. À travers le théorème de Pythagore, il s'ensuit que:

|V|² = (V_X)² +  (V_et)²

Forme polaire d'un vecteur

Lorsque l'ampleur du vecteur est connue |V| Et l'angle θ que cette forme avec l'axe de référence, généralement l'axe horizontal, le vecteur est également spécifié. On dit alors que le vecteur est exprimé sous forme polaire.

Les composants rectangulaires dans ce cas sont facilement calculés:

V_X = |V|.cos θ

V_et = |V|.sin θ

Selon ce qui précède, les composants rectangulaires du vecteur de vitesse V de l'avion serait:

V_X = 850 . cos 45º km / h = 601.04 km / h

V_et = 850 . Sen 45º km / h = 601.04 km / h

Gars

Il existe différents types de vecteurs. Il y a des vecteurs de veine, la position, le déplacement, la force, le champ électrique, la quantité de mouvement et bien d'autres. Comme nous l'avons déjà dit, en physique, il y a beaucoup d'amplitudes vectorielles.

Quant aux vecteurs qui ont certaines caractéristiques, nous pouvons mentionner les types de vecteurs suivants:

-Nul: Ce sont des vecteurs dont l'ampleur est 0 et qui sont désignés comme 0. N'oubliez pas que la lettre audacieuse symbolise les trois caractéristiques fondamentales d'un vecteur, tandis que la lettre normale représente uniquement le module.

Par exemple, sur un corps en équilibre statique, la somme des forces doit être un vecteur nul.

-Gratuit et lié: Les vecteurs gratuits sont ceux dont les points d'origine et d'arrivée sont toutes les paires de points de l'avion ou de l'espace, contrairement aux vecteurs liés, dont l'origine coïncide avec celle du système de référence utilisé pour les décrire.

La paire ou le moment produit par quelques forces est un bon exemple de vecteur gratuit, car le couple ne s'applique pas à un point particulier.

-Équipement: Ce sont deux vecteurs gratuits qui partagent des caractéristiques identiques. Par conséquent, ils ont la même ampleur, la même direction et le même sens.

-Coplanares ou coplanarios: vecteurs qui appartiennent au même plan.

-Opposés: vecteurs avec une ampleur et une direction égales, mais les sens opposés. Le vecteur opposé à un vecteur V C'est le vecteur -V Et la somme des deux est le vecteur nul: V + (-V) = 0.

-Concurrent: vecteurs dont les lignes d'action passent tous par le même point.

-Glisser: Ces vecteurs dont le point d'application peuvent glisser le long d'une ligne particulière.

-Coménéal: vecteurs situés sur la même ligne.

-Unitaires: Ces vecteurs dont le module est 1.

Vecteurs unitaires orthogonaux

Il existe un type de vecteur très utile en physique appelé vecteur d'unité orthogonal. Le vecteur d'unité orthogonal a un module égal à 1 et les unités peuvent être n'importe laquelle, par exemple celles de la vitesse, de la position, de la force ou autre.

Il existe un ensemble de vecteurs spéciaux qui aident à représenter facilement d'autres vecteurs et à effectuer des opérations avec eux: ce sont les vecteurs d'unité orthogonaux Toi, J et k, Unitaires et perpendiculaires les uns aux autres.

En deux dimensions, ces vecteurs sont dirigés tout au long du sens positif des deux axes X comme l'axe et. Et en trois dimensions, un vecteur unitaire est ajouté dans le sens de l'axe z positif. Ils sont représentés comme suit:

Peut vous servir: quelle est la structure de la recherche documentaire?

Toi =

J =

k =

Un vecteur peut être représenté par des vecteurs unitaires Toi, J et k comme suit:

V = V_X Toi + V_et J + V_z k

Par exemple le vecteur de vitesse V D'après les exemples précédents, vous pouvez écrire en tant que:

V = 601.04 Toi + 601.04 J km / h

Le composant dans k Ce n'est pas nécessaire, car ce vecteur est dans l'avion.

Somme des vecteurs

La somme des vecteurs apparaît très fréquemment dans diverses situations, par exemple lorsque vous souhaitez trouver la force résultante sur un objet affecté par diverses forces. Pour commencer, supposer que vous avez deux vecteurs gratuits ou et V dans l'avion, comme le montre la gauche suivante:

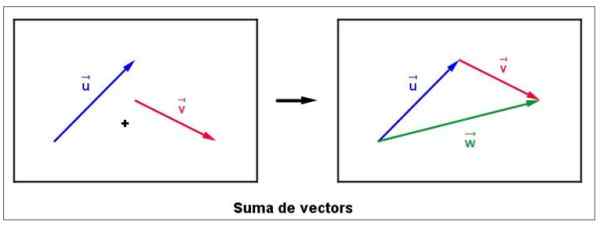Figure 4. Somme graphique de deux vecteurs. Source: Wikimedia Commons. Lluc Cabanach [cc by-sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)].

Il déménage immédiatement vers le vecteur V, sans modifier son ampleur, sa direction ou son sens, de sorte qu'il provient coïncide avec la fin de ou.

Le vecteur de somme est appelé W et est tiré à partir de u se terminant par V, Selon la bonne figure. Il est important de noter que l'ampleur du vecteur W Ce n'est pas nécessairement la somme des amplitudes de V et ou.

S'il se reflète soigneusement à cet égard, la seule occasion où l'ampleur du vecteur résultant est la somme des amplitudes des addeds, c'est lorsque les deux toxicomanes sont dans le même sens et ont la même signification.

Et que se passe-t-il si les vecteurs ne sont pas libres? Il est également très facile de les ajouter. La voie à faire est d'ajouter des composants de composants ou une méthode analytique.

Par exemple, considérons les vecteurs de la figure suivante, la première chose est de les exprimer à partir de l'une des formes cartésiennes expliqué précédemment:

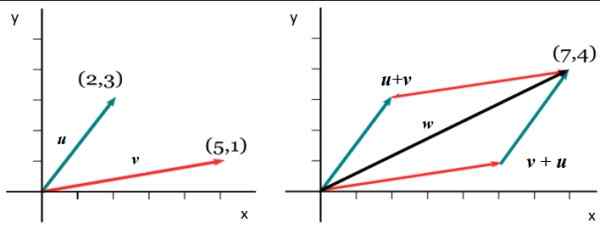Figure 5. Somme de deux vecteurs liés. Source: Wikimedia Commons.

V =

ou =

Pour obtenir le composant dans X du vecteur ajoute W, Les composants respectifs sont ajoutés X de V et ou: W_X = 5 + 2 = 7. Et pour obtenir W_et Une procédure analogue est suivie: w_et = 1 + 3. Donc:

ou =

Propriétés de la somme des vecteurs

-La somme de deux vecteurs ou plus se traduit par un autre vecteur.

-Il est commutatif, l'ordre des ajouts ne modifie pas la somme, de sorte que:

ou + V = V + ou

-L'élément neutre de la somme des vecteurs est le vecteur nul: V + 0 = V

-La soustraction de deux vecteurs est définie comme la somme de l'inverse: v - u = V + (-ou)

Exemples de vecteurs

Comme nous l'avons dit, il existe de nombreuses quantités vectorielles en physique. Parmi les plus connus figurent:

-Position

-Déplacement

-Vitesse moyenne et vitesse instantanée

-Accélération

-Force

-Quantité de mouvement

-Couple ou moment de force

-Impulsion

-Champ électrique

-Champ magnétique

-Moment magnétique

D'un autre côté, ce ne sont pas des vecteurs mais de l'escalade:

-Temps

-Masse

-Température

-Volume

-Densité

-Travail mécanique

-Énergie

-Chaleur

-Pouvoir

-Tension

-Courant électrique

Autres opérations entre les vecteurs

En plus de la somme et de la soustraction des vecteurs, il existe trois autres opérations entre les vecteurs très importants, car ils donnent naissance à de nouvelles amplitudes physiques très importantes:

-Produit d'un scalaire pour un vecteur.

-Le produit scalaire ou le produit ponctuel entre les vecteurs

-Et le produit croisé ou vecteur entre deux vecteurs.

Produit d'un scalaire pour un vecteur

Considérez la deuxième loi de Newton, qui stipule que cette force F et accélération pour Ils sont proportionnels. La constante de proportionnalité est la masse m de l'objet donc:

F = m.pour

La pâte est un scalaire; Pour sa part, la force et l'accélération sont des vecteurs. Comme la force est obtenue en multipliant la masse par l'accélération, il est le résultat du produit d'un scalaire par un vecteur.

Peut vous servir: exemples de cadre théorique

Ce type de produit se traduit toujours par un vecteur. Ici un autre exemple: la quantité de mouvement. Être P La quantité vectorielle de mouvement, V Le vecteur de vitesse et comme toujours, m est la masse:

P = m.V

Produit scalaire ou produit ponctuel entre les vecteurs

Nous avons placé des travaux mécaniques dans la liste des amplitudes qui ne sont pas des vecteurs. Cependant, le travail en physique est le résultat d'une opération entre les vecteurs appelée produit scalaire, produit interne ou produit ponctuel.

Être les vecteurs V et ou, Le produit de point ou d'escalade est défini entre eux:

V∙ou = |V| ∙ |ou |.cos θ

Étant θ l'angle entre eux. À partir de l'équation montrée, il est immédiatement déduit que le résultat du produit ponctuel est un scalaire et aussi que si les deux vecteurs sont perpendiculaires, leur produit scalaire est 0.

Retour au travail mécanique W, C'est le produit scalaire entre le vecteur de résistance F et le déplacement vectoriel ℓ.

W = F∙ℓ                  

Lorsque des vecteurs sont disponibles en termes de leurs composants, le produit ponctuel est également très simple à calculer. Ouais V = X, V_et, V_z > et ou = X, ou_et, ou_z >, Le produit ponctuel entre les deux est:

V∙ou = V_X ou_X + V_et ou_et + V_z ou_z

Le produit ponctuel entre les vecteurs est donc commutatif:

V∙ou = ou∙V

Produit croisé ou produit vectoriel entre les vecteurs

Ouais V Et vous êtes nos deux exemples de vecteurs, le produit vectoriel est défini comme:

V X ou = W

Il s'ensuit immédiatement que le produit croisé se traduit par un vecteur, dont le module est défini comme:

|V X u | = | V | . | u |. sin θ

Où θ C'est l'angle entre les vecteurs.

Le produit croisé n'est pas commutatif, donc V X u ≠ u X V. En fait V X U = - (u X V).

Si les deux exemples de vecteurs sont exprimés en termes de vecteurs unitaires, le calcul du produit vectoriel est facilité:

V = V_X Toi + V_et J + V_z k

ou = u_X Toi + ou_et J + ou_z k

Traverser les produits entre les vecteurs unitaires

Le produit croisé entre les vecteurs unitaires identiques est nul, car l'angle entre eux est de 0º. Mais parmi différents vecteurs unitaires, l'angle entre eux est de 90 ° et du péché 90º = 1.

Le schéma suivant aide à trouver ces produits. En direction de la flèche, il a un sens positif et dans la direction opposée:

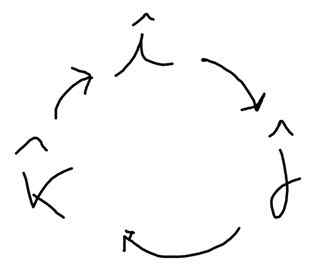
Toi X J = K, J X k = Yo; k X Toi = J; J X i = -k; k X J = -Yo; Toi X k = -J

Appliquer une propriété distributive, qui reste valable pour les produits parmi les vecteurs plus les propriétés des vecteurs unitaires, vous avez:

V X ou = (V_X Toi + V_et J + V_z k) X (u_X Toi + ou_et J + ou_z k) =  

= (V_etou_z - V_zou_et )Toi + (V_zou_X - V_Xou_z )J + (V_Xou_et - V_etou_X )k

Exercices résolus

- Exercice 1

Compte tenu des vecteurs:

V = -5 Toi + 4J + 1 k

ou = 2 Toi -3 J + 7k

Quel devrait être le vecteur W pour que la somme V + ou + W résultats 6 Toi +8 J -dixk?

Solution

-5 Toi + 4J + 1 k

2 Toi -3 J + 7k

 W_X Toi + W_et J + W_z k  +

--

6Toi + 8 J -dix k

Par conséquent, il faut accomplir que:

-5 +2 + W_X = 6 → W_X = 9

4-3 + W_et = 8 → W_et = 7

1 + 7 + W_z = -10 → W_z = -18

La réponse est: W = 9 Toi +7 J - 18k

- Exercice 2

Quel est l'angle entre les vecteurs V et ou de l'exercice 1?

Solution

Nous utiliserons le produit scalaire. Nous avons:

cos θ = V∙ou / |V| ∙ |ou|

V∙ou= -10 -12 + 7 = -15

|V| = √ (-5)² +4² +1²= √42 = 6.48

|ou| = √2² +(-3)² +7²= √62 = 7.87

Remplacement de ces valeurs:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.1er

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
2. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
3. Rex, un. 2011. Fondamentaux de la physique. Pearson.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
5. SERAY, R., Jewett, J. 2008. Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.