Concept de variation linéaire, exemples, exercice résolu

La Variation linéaire Il se produit entre deux amplitudes physiques lorsque le graphique qui les représente est une ligne droite. Il équivaut à affirmer que les variables sont en dépendance linéaire, de sorte que si l'un d'eux nous l'appelons "y" et l'autre "x", ils seront liés par l'expression mathématique:

y = mx + b

Dans cette formule, M et B sont des nombres réels. La valeur de m représente la pente ou l'inclinaison de la ligne - qui est toujours constante - et b est la coupe de la ligne avec l'axe vertical.

La variation linéaire d'une ampleur par rapport à un autre signifie que son graphique est une ligne droite. Source: JoulerGio / CC By-S (https: // CreativeCommons.Org / licences / by-sa / 4.0)

Chaque phénomène qui répond à une variation linéaire a des noms différents pour les variables, comme nous le verrons dans les exemples suivants. Cependant, la forme mathématique de l'équation est la même.

Expérimentalement peut être établi s'il existe une relation linéaire entre deux amplitudes, mesurer les couples de valeurs (x, y).

Les points obtenus sont graphiques dans un papier millimètre et sont observés s'ils ont une tendance linéaire, c'est-à-dire s'il y a une ligne qui s'adapte adéquate aux données expérimentales.

Dans le premier cas, cette ligne peut être tracée visuellement, mais au moyen d'un régression linéaire Ils peuvent être trouvés analytiquement, les valeurs de m et b de la ligne qui correspondent le mieux aux points expérimentaux.

[TOC]

Exemples de variation linéaire

Il existe de nombreux phénomènes naturels, ainsi que des relations établies entre les modèles de mesure, qui obéissent à une variation linéaire, par exemple:

Vitesse dans le mouvement rectiligne uniformément varié

La vitesse en fonction du temps V (t) d'un mobile qui se déplace le long d'une ligne avec une accélération constante à et la vitesse initiale V_soit  différent de 0. Ce mouvement est connu comme Mouvement rectiligne uniformément varié Et l'équation de vitesse est:

Peut vous servir: densité

v (t) = v_soit + À

Dilatation thermique

Un autre phénomène naturel dont la variation est linéaire est l'augmentation de la longueur qui éprouve une tige ou un fil lorsqu'il est chauffé.

En effet, lorsque la température de n'importe quel objet augmente, ses dimensions également, et cette augmentation dépend du changement de température ΔT et d'une quantité appelée Coefficient de dilatation linéaire indiqué par la lettre grecque α:

L = L_soit + α Δt

Dans cette expression, la longueur finale de l'objet et L_soit est sa longueur initiale.

Position d'un mobile à vitesse constante

Un mobile avec vitesse constant se déplace toujours en ligne droite. Si la ligne droite est l'axe horizontal x, la position x (t) à tout moment est donnée par:

x (t) = x_soit + Vermont

Où x_soit C'est la position initiale, v est la vitesse et t est le temps. De cette façon, il est dit que la position X varie linéairement avec le temps t.

Une stature de personne

Les médecins et les anthropologues peuvent estimer la stature d'une personne en mesurant la durée du fémur.

Plus une personne est élevée, plus les jambes sont longues, donc il existe des modèles linéaires pour prédire la hauteur d'une personne adulte H (en pouces) si la longueur L (également en pouces) de son fémur est connue, selon l'équation:

H = 1.880⋅l + 32.010

Échelles de température

Les échelles Celsius et Fahrenheit sont utilisées quotidiennement pour mesurer les températures. Cette dernière échelle est couramment utilisée dans les pays en anglais. Il y a une équivalence pour se déplacer de l'un à l'autre:

F = (9/5) C + 32

Où f est la température en degrés Fahrenheit et C est la température en degrés Celsius.

Pression et profondeur

La pression absolue P dans un fluide incompressible tel que l'eau, dont la densité constante est ρ, varie en fonction de la profondeur H comme:

Il peut vous servir: tir horizontal: caractéristiques, formules et équations, exercices

P = P_soit + ρgh

Où p_soit C'est la pression sur la surface libre du liquide. Si le liquide est dans un récipient ouvert à l'atmosphère, cette pression est simplement la pression atmosphérique P_{AU M}, Pouvoir écrire alors:

P = P_{AU M} + ρgh

La pression atmosphérique au niveau de la mer est d'environ 101 kPa. Cette relation entre P et H signifie que la pression augmente linéairement avec la profondeur.

La pression subie par le plongeur varie linéairement avec la profondeur. Source: Ahmed Samy / Pexels.

Exercice résolu

Coût de conduite

Le coût mensuel C de la gestion d'une voiture comprend un coût fixe mensuel C_soit plus le coût du kilométrage ou le kilométrage parcouru chaque mois. Un conducteur observe que dans un mois, le coût de gestion était de 380 $ pour 480 $, et le mois suivant, il était de 460 $ par 800 miles.

Que le nombre de miles soit parcouru par mois par le conducteur, avec les données fournies, trouver:

a) La variation linéaire entre C et D.

b) Combien la voiture coûterait par mois pour un voyage de 1500 milles?

c) le graphique de C versus d.

Solution à

Supposons que les variables aient une relation donnée par:

C = C_soit + POUR.d

Où a et c_soit Ils sont constants pour déterminer. A est la pente de la ligne qui représente graphiquement la relation entre C et D. CO est la coupe avec l'axe vertical, le coût fixe mensuel que le conducteur doit payer pour le simple fait d'avoir la voiture disponible. Ici, les coûts de maintenance et d'imposition peuvent être inclus, par exemple.

Pour déterminer sans équivoque une ligne, il est nécessaire de connaître sa pente. Pour cela, nous avons les points:

P₁: 480 miles, 380 $

P₂: 800 miles, 460 $

Ces points, de coordonnées (d, c) ou (distance, coût) sont analogues aux points de coordonnées (x, y) du plan cartésien, quels changements sont les noms. La pente de la ligne est alors donnée par:

Peut vous servir: plan incliné

A = (c₂ - C₁)/(D₂ - d₁)

A = [(460 - 380) $ / (800 - 480) miles] = (1/4) $ / mile

La pente de la ligne représente le coût par mile, de cette manière:

C = C_soit + POUR.D = CO + (1/4).d

Pour déterminer le coût de base C_soit Cette équation est prise et l'un des points que nous connaissons lui appartient, par exemple p₁:

380 $ = c_soit + [(1/4) $ / mile] . 480 mile → 380 $ = c_soit + 120 $

C_soit = 260 $

Nous pouvons maintenant formuler le modèle de variation linéaire tel que:

C = 260 + (1/4) D

Solution B

Le coût mensuel du déplacement de 1500 miles est:

C = 260 + (1/4) x 1500 $ = 635 $

Solution C

Le graphique de C en fonction de D est:

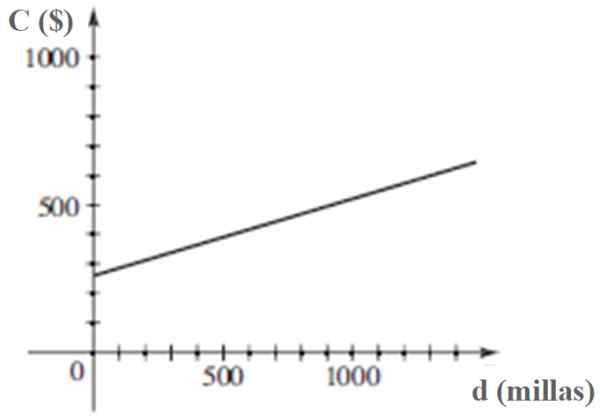Le coût C de la manipulation d'un véhicule est une fonction linéaire de la distance parcourue d. Source: Stewart, J. Précalation.

Les références

1. Baldor. 1977. Algèbre élémentaire. Éditions culturelles vénézuéliennes.
2. Hoekenga, C. Équations linéaires en science. Récupéré de: VisionLearning.com.
3. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
4. Jiménez, R. 2008. Algèbre. Prentice Hall.
5. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
6. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.