Caractéristiques variables continues, exemples et exercices

La Variable continue C'est celui qui peut prendre un nombre infini de valeurs numériques entre deux valeurs données, même si ces deux valeurs sont arbitrairement fermées. Ils sont utilisés pour décrire les attributs mesurables; par exemple la taille et le poids. Les valeurs prises par une variable continue peuvent être des nombres rationnels, des nombres réels ou des nombres complexes, bien que ce dernier cas soit moins fréquent en statistique. 

La principale caractéristique des variables continues est qu'entre deux valeurs rationnelles ou réelles peuvent toujours être trouvées, et entre cet autre et le premier peut trouver une autre valeur, et donc indéfiniment.

Figure 1. La courbe représente une distribution continue et les barreaux sont discrets. Source: Pixabay

Par exemple, supposons la variable de poids dans un groupe où le poids le plus important a 95 kg et le poids le plus bas de 48 kg; Ce serait la plage de la variable et le nombre de valeurs possibles est infinie.

Par exemple entre 50,00 kg et 50,10 kg peut être de 50,01. Mais entre 50,00 et 50,01, la mesure peut être de 50 005. C'est une variable continue. D'un autre côté, si dans le poids possible, une seule précision décimale était établie, la variable utilisée serait discrète.

Les variables continues appartiennent à la catégorie des variables quantitatives, car elles ont une valeur numérique associée. Avec cette valeur numérique, il est possible d'effectuer des opérations mathématiques allant de l'arithmétique aux méthodes de calcul infinitésimal. 

[TOC]

Exemples

La plupart des variables de la physique sont des variables continues, parmi lesquelles nous pouvons nommer: longueur, temps, vitesse, accélération, énergie, température et autres.

Variables continues et variables discrètes

En statistiques, divers types de variables peuvent être définis, à la fois qualitatifs et quantitatifs. Les variables continues appartiennent à cette dernière catégorie. Avec eux, il est possible d'effectuer des opérations arithmétiques et de calcul.

Par exemple la variable H, Correspondant aux personnes avec une hauteur entre 1,50 m et 1,95 m, c'est une variable continue. 

Comparons cette variable avec cet autre: le nombre de fois coûteux dans le lancement d'une monnaie, que nous appellera n.

La variable n Vous pouvez cependant prendre des valeurs entre 0 et Infinity n Ce n'est pas une variable continue car elle ne peut pas prendre la valeur 1.3 ou 1,5, car entre les valeurs 1 et 2, il n'y a pas d'autre. Ceci est un exemple de Variable discrète.

Exercice de variables continues

Considérez l'exemple suivant: Une machine produit des matchs de phosphore et les emballez dans sa boîte. Deux variables statistiques sont définies:

Peut vous servir: processus isobare: formules, équations, expériences, exercices

Variable 1: L = longueur de pliage.

Variable 2: n = nombre de porcs par boîte.

La longueur nominale des correspondances est de 5,0 cm avec une tolérance de 0,1 cm. Le nombre de porcs par boîte est de 50 avec une tolérance de 3.

a) Indiquez la plage de valeurs qui peuvent prendre L et N.

b) Combien de valeurs pouvez-vous prendre L?

c) Combien de valeurs pouvez-vous prendre n?

Disons dans chaque cas s'il s'agit d'une variable discrète ou continue.

Solution

Les valeurs de L Ils sont compris dans l'intervalle [5,0-0.1; 5,0 + 0,1]; c'est-à-dire que la valeur de L est dans l'intervalle [4,9 cm; 5,1 cm] et la variable L Vous pouvez prendre des valeurs infinies entre ces deux mesures. C'est alors une variable continue.

La valeur de la variable n est dans l'intervalle [47; 53]. La variable n Il ne peut prendre que 6 valeurs possibles dans l'intervalle de tolérance, c'est alors une variable discrète.

Exercer distribution de probabilité

Si, en plus d'être continu, les valeurs prises par la variable ont associé une certaine probabilité d'occurrence, alors c'est un Variable aléatoire continue. Il est très important de distinguer si la variable est discrète ou continue, car les modèles probabilistes s'applicables les uns aux autres sont différents.

Une variable aléatoire continue est complètement définie lorsque les valeurs qu'ils peuvent supposer sont connues, et la probabilité que chacun d'eux doit se produire.

-Exercice 1 des probabilités

L'usine de correspondance les rend de telle manière que la longueur des bâtons se situe toujours entre les valeurs de 4,9 cm et 5,1 cm, et zéro de ces valeurs. Il y a la probabilité d'obtenir un bâton qui mesure entre 5,00 et 5,05 cm, bien que nous puissions également extraire l'un des 5.0003 cm. Ces valeurs sont-elles également probables?.

Peut vous servir: densité relative: calcul, exemples, exercices

Solution

Supposons que la densité de probabilité est uniforme. Ensuite, les chances de trouver un phosphore avec une certaine longueur sont répertoriées:

-Qu'un phosphore se trouve dans la gamme [4,9; 5,1] a une probabilité = 1 (ou 100%), car la machine ne retire pas les correspondances de ces valeurs.

-Trouver un phosphore entre 4,9 et 5,0 a une probabilité = ½ = 0,5 (50%), car il s'agit de la moitié de la plage de longueurs.

-Et la probabilité que la correspondance ait une longueur entre 5,0 et 5,1 est également de 0,5 (50%)

-On sait qu'il n'y a pas de bâtons de phosphore qui ont une longueur entre 5,0 et 5,2. Probabilité: zéro (0%).

Probabilité de trouver un bâton dans une certaine gamme

Maintenant observons les probabilités suivantes p pour obtenir des bâtons dont la longueur est entre L₁ et moi₂:

 P = (l₂ -l₁) / (L_Max - L_min)

-P qu'une correspondance a une longueur entre 5,00 et 5,05 est indiquée comme P ([5,00; 5.05]):

P ([5,00; 5,05]) = (5,05 - 5,00) / (5,1 - 4,9) = 0,05 / 0,2 = ¼ = 0,25 (25%)

-P que le Cerrillo a une longueur entre 5,00 et 5,01 est:

P ([5,00; 5,01]) = (5,00 - 5,01) / (5,1 - 4,9) = 0,01 / 0,2 = 1/20 = 0,05 (5%)

-P que le Cerrillo a une longueur entre 5 000 et 5 001 est encore plus bas:

P (5 000; 5 001) = 0,001 / 0,2 = 1/200 = 0,005 (0,5%)

Si nous continuons à diminuer l'intervalle pour approcher de plus en plus à 5,00, la probabilité qu'un bâton ait exactement 5,00 cm est nul (0%). Ce que nous avons, c'est la probabilité de trouver une correspondance dans une certaine plage.

Probabilité de trouver plusieurs bâtons dans une certaine gamme

Si les événements sont indépendants, la probabilité que deux bâtons soient dans une certaine plage est le produit de leurs probabilités.

-La probabilité que deux bâtons se situent entre 5,0 et 5,1 est de 0,5 * 0,5 = 0,25 (0,25%)

-La probabilité que 50 bâtons se situent entre 5,0 et 5,1 est (0,5) ^ 50 = 9 × 10 ^ -16, c'est presque nulle.

-La probabilité que 50 bâtons se situent entre 4,9 et 5,1 est (1) ^ 50 = 1 (100%)

-Exercice 2 des probabilités

Dans l'exemple précédent, l'hypothèse a été faite que la probabilité est uniforme dans l'intervalle donné, mais ce n'est pas toujours le cas.

Peut vous servir: pression hydrostatique: formule, calcul, exemples, exercices

Dans le cas de la machine réelle qui produit les bâtons, la possibilité que le bâton soit dans la valeur centrale est supérieure à l'une des valeurs extrêmes. Du point de vue mathématique, il est modélisé avec une fonction f (x) connue sous le nom de densité de probabilité.

La probabilité que la mesure soit entre a et b est calculée par l'intégrale définie de la fonction f (x) entre a et b. 

À titre d'exemple, supposons que nous voulons trouver la fonction F (x), qui représente une distribution uniforme entre les valeurs 4.9 et 5.1 de l'exercice 1. 

Si la distribution de probabilité est uniforme, alors f (x) est égal à la constante C, qui est déterminée en prenant l'intégrale entre 4,9 et 5,1 de C. Comme cette intégrale est la probabilité, le résultat doit donc être 1.

Figure 2. Densité de probabilité uniforme. (Élaboration propre)

Ce qui signifie que c vaut 1 / 0,2 = 5. En d'autres termes, la fonction de densité de probabilité uniforme est f (x) = 5 si 4.9≤x≤5.1 et 0 de cette gamme. La figure 2 montre une fonction de densité de probabilité uniforme.

Remarque Comme dans les intervalles de la même largeur (par exemple 0,02), la probabilité est la même au centre qu'à la fin de la plage variable continue L (Longueur de cornichon).

Un modèle plus réaliste serait une fonction de densité de probabilité comme suit:

-f (x) = -750 ((x-5.0) ^ 2-0,01) Si 4.9≤x≤5,1

-0 en dehors de cette gamme 

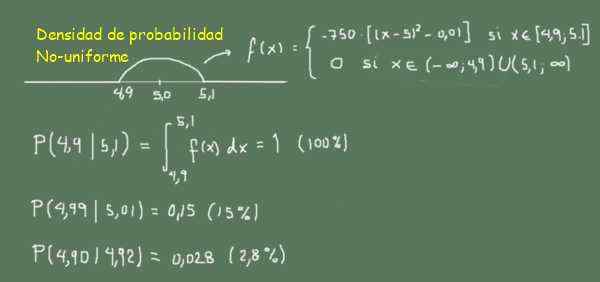figure 3. Fonction de densité de probabilité non uniforme. (Élaboration propre)

Dans la figure 3, il peut être observé comme la probabilité de trouver des bâtons entre 4,99 et 5,01 (largeur 0,02) que la recherche de bâtons entre 4,90 et 4,92 (largeur 0,02)

Les références

1. Dinov, Ivo. Variables aléatoires discrètes et distributions de probabilité. Récupéré de: stat.Ucla.Édu
2. Variables aléatoires discrètes et continues. Récupéré de: OCW.mit.Édu
3. Variables aléatoires discrètes et distributions de probabilité. Récupéré de: page d'accueil.Ddms.Uiowa.Édu
4. H. Peshro. Introduction à la probabilité. Récupéré de: Cours de probabilité.com
5. Mendenhall, w. 1978. Statistiques pour l'administration et l'économie. Groupe éditorial ibero-américain. 103-106.
6. Problèmes variables aléatoires et modèles de probabilité. Récupéré de: ugr.est.
7. Wikipédia. Variable continue. Récupéré de Wikipedia.com
8. Wikipédia. Variable statistique. Récupéré de Wikipedia.com.