Valeur relative

Quelle est la valeur relative d'un nombre?

Il valeur relative d'un nombre o Le chiffre du système décimal dépend de la position qu'elle occupe lorsqu'elle fait partie d'un chiffre. Par conséquent, on dit que c'est une valeur de position. Un exemple très simple: le valeur relative de 1 Au numéro 123, Ce sera 100, Parce que 1 occupe la position des centaines.

Autre exemple: le numéro 58 est formé par les chiffres 5 et 8. En examinant ce chiffre de droite à gauche, la valeur relative de 8 est de 8, pour être en position des unités et la valeur relative de 5 est de 50, pour occuper le site des dizaines. Le nombre est lu "cinquante-huit".

D'un autre côté, les mêmes chiffres ont des valeurs relatives différentes dans le nombre 85, car ils ont échangé des positions. En commençant de droite à gauche, la valeur relative de 5 dans ce cas est de 5, la valeur relative de 8 est de 80 et le nombre est lu "quatre-vingt-cinq".

Comment trouver la valeur relative d'un nombre?

La procédure générale pour trouver la valeur relative de chaque chiffre est la suivante:

• Le premier chiffre de droite à gauche est en position des unités et leur valeur est multipliée par 1.
• Le chiffre suivant correspond aux dizaines et est multiplié par 10.
• La position suivante correspond aux centaines et la valeur du chiffre est multipliée par 100.
• La position suivante est mille, donc le chiffre est multiplié par 1000.

Et ainsi de suite pour des nombres plus grands, multipliant le chiffre par la puissance 10 correspondante: 100000, 100000 et au-delà.

Par exemple, le numéro 321 peut être écrit comme 3 * 100 + 2 * 10 + 1 * 1, ou équivalent 300 + 20 + 1. Dans l'exemple précédent, on peut rapidement voir que la valeur relative de 3 est de 300, 2 est 20 et 1 est 1.

Peut vous servir: propriété distributive

Exemples de valeurs relatives

Numéro 727

Pour déterminer la valeur relative d'un chiffre, vous devez être guidé par le principe de base suivant de la numérotation écrite du système décimal:

Tout chiffre à gauche d'un autre représente une unité 10 fois plus élevée, et vice versa: chaque chiffre à droite d'un autre, représente une unité 10 fois plus petite. 

Par exemple, la figure 727, qui se lit «sept cent vingt-sept», se compose de chiffres 2 et 7, avec 7 répétitions, mais occupant des positions différentes.

En lisant 727 de droite à gauche, il est observé que le 7 à droite occupe la position de l'unité, donc il est multiplié par 1:

7 x 1 = 7

Et sa valeur relative est 7.

Le chiffre 2 au milieu occupe la position des dizaines et pour trouver leur valeur relative, il est multiplié par 10:

2 x 10 = 20

Enfin sur le 7 à l'extrême gauche a la position des centaines. Alors vous devez multiplier par 100 et sa valeur relative est:

7 x 100 = 700

Notez que ce n'est que lorsque le chiffre occupe la position de l'unité est que sa valeur absolue et sa valeur relative sont égales. Par conséquent, si la valeur relative du nombre est VR et que sa valeur absolue est VA, la formule générale pour trouver la valeur relative est:

VR = valeur absolue VA × valeur de sa position

Une figure peut être écrite comme la somme des valeurs relatives de ses chiffres, c'est ce qu'on appelle notation développée. Poursuivant avec l'exemple du numéro 727, vous devez:

727 = 700 + 20 + 7

Et si vous préférez utiliser les pouvoirs de 10, le nombre 727 est également exprimé équivalent comme:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Il peut vous servir: Multiples of 8: Que sont et explications

Où les exposants de la puissance basés sur 10 représentent la position de chaque chiffre et sont appelés Indices. Dans la figure suivante, un autre exemple est illustré.

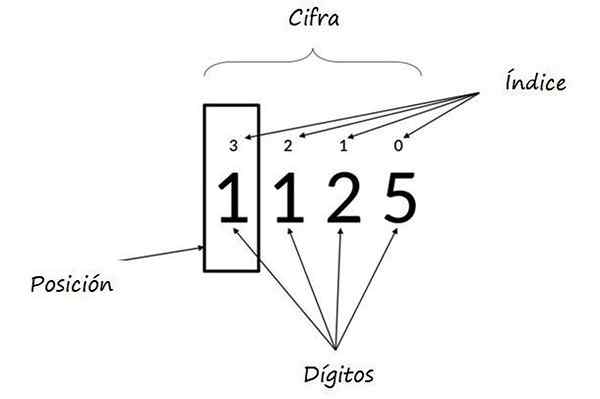Dans le nombre 1125, la valeur relative de 5 est de 5, le 2 est 20, le 1 est 100 et le 1 gauche dans la boîte est 1000. Source: Wikimedia Commons.

Numéro 63

En partant de gauche à droite, le 3 est donc en position des unités:

Valeur relative de 3: 3 x 1 = 3

Quant à 6, c'est dans la position des dizaines, alors:

Valeur relative de 6: 6 x 10 = 60

Numéro 603

Cette figure est différente de la précédente, car bien que la valeur relative de 0 soit 0, les autres chiffres ont des valeurs relatives différentes. Partant de droite à gauche comme toujours:

• Valeur relative de 3: 3 x 1 = 3
• Valeur relative de 0: 0 x 10 = 0
• Valeur relative de 6: 6 x 100 = 600

Numéro 630

Dans ce cas, 0 est en position des unités:

• Valeur relative de 0: 0 x 1 = 0
• Valeur relative de 3: 3 x 10 = 30
• Valeur relative de 6: 6 x 100 = 600

Exercices résolus

Exercice 1

Indiquez la valeur relative des nombres soulignés:

a) 1209

b) 2782

c) 376

d) 3045

E) 273

Solution

a) Le chiffre 1 sur 1209 occupe la position des milliers ou des milliers. Par conséquent, sa valeur relative est de 1000.

VR (1) = 1 x 1000 = 1000

b) Le 2 occupe la position des unités en 2782, donc sa valeur relative est 2.

c) En 376, le 7 est en position des dizaines et:

VR (7) = 7 x 10 = 70.

d) En 3045, le 4 est également en position des dizaines:

VR (4) = 4 x 10 = 40.

e) En 273, le 3 est à la place des unités et leur valeur relative coïncide avec la figure du chiffre, c'est-à-dire:

Peut vous servir: pyramide hexagonale

Vr (3) = 3 x 1 = 3

Exercice 2

Écrivez le nombre le plus bas de 5 chiffres, sans aucun est répété et remplissez les conditions suivantes:

a) que tous les chiffres sont différents

b) il a un 7 sur le mille

c) Le 8 est en position des unités.

Solution à

Le plus petit numéro de 5 chiffres, avec tous, doit commencer par 1, car bien que 0 soit inférieur, car le premier chiffre à gauche ne compte pas, le nombre recherché est donc:

10234

Solution B

La position Millar pour 7 correspond à 7000, mais comme vous voulez le plus petit chiffre possible qui contient 5 chiffres, le nombre doit commencer par 1, suivi de 7 puis 023 dans les positions restantes, car aucun chiffre ne doit être répété.

Par conséquent, le nombre est:

17023

Solution C

Comme demandé que les 8 soient en position des unités, ce doit être à l'extrême droite. Étant le nombre le moins possible, sans que ses 5 chiffres soient répétés, le nombre recherché est:

10238

Exercice 3

Calculez la valeur absolue et relative (de chaque figure) du nombre 579.

Solution

Il a que 579 est égal à 5 ​​× 100 + 7 × 10 + 9 × 1, ou équivalent, il est égal à 500 + 70 + 9. Par conséquent, la valeur relative de 5 est de 500, la valeur relative de 7 est de 70 et le 9 est 9.

D'un autre côté, la valeur absolue de 579 est égale à 579.

Exercice 4

Donnez le numéro 9.648.736, quelle est la valeur relative de 9 et 6 (de gauche à droite)? Quelle est la valeur absolue du nombre donné?

Solution

En réécrit au numéro 9.648.736 Il est obtenu que cela équivaut à

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

ou vous pouvez écrire comme

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

De sorte que la valeur relative de 9 est 9.000.000 et la valeur relative des 6 premiers est 600.000.

D'un autre côté, la valeur absolue du nombre donné est 9.648.736.