Caractéristiques ovales (figure géométrique), exemples, exercices

Il ovale Symétrique est définie comme une courbe plate et fermée, qui a deux axes de symétrie perpendiculaire - un majeur et un mineur - et est composé de deux arches de cercle égales deux à deux à deux à deux à deux à deux à deux à deux à deux.

De cette façon, vous pouvez dessiner à l'aide d'une boussole et quelques points de référence sur l'un des axes de symétrie. En tout cas, il y a plusieurs façons de le dessiner, comme nous le verrons plus tard.

Figure 1. Vue du Colosseum de Rome, un exemple de forme ovale en architecture. Source: Pixabay.

C'est une courbe très familière, car elle est reconnue comme le contour d'une ellipse, ce qui est un cas particulier de l'ovale. Mais l'ovale n'est pas une ellipse bien qu'elle semble parfois beaucoup, car ses propriétés et tracé diffèrent. Par exemple, l'ellipse n'est pas construite avec une boussole.

[TOC]

Caractéristiques

L'Ovale a des applications très variées: l'architecture, l'industrie, la conception graphique, l'horlogerie et les bijoux ne sont que quelques domaines où son utilisation se démarque.

Les caractéristiques les plus remarquables de cette courbe importante sont les suivantes:

-Il appartient au groupe de courbes techniques: il est tracé en formant des arcs de circonférence à l'aide d'une boussole.

-Tous ses points sont sur le même plan.

-Il manque de courbes ou de liens.

-Sa disposition est continue.

-La courbe ovale doit être douce et convexe.

-Lorsque vous tracez une ligne tangente vers l'ovale, tout est du même côté de la ligne.

-Un ovale prend en charge deux tangentes parallèles à la plupart.

Exemples

Il existe plusieurs méthodes pour construire des ovales qui nécessitent l'utilisation de la règle, de l'équipe et de la boussole. Ensuite, nous mentionnerons certains des plus utilisés.

Peut vous servir: inégalité du triangle: démonstration, exemples, exercices résolus

Construction d'un ovale par les circonférences concentriques

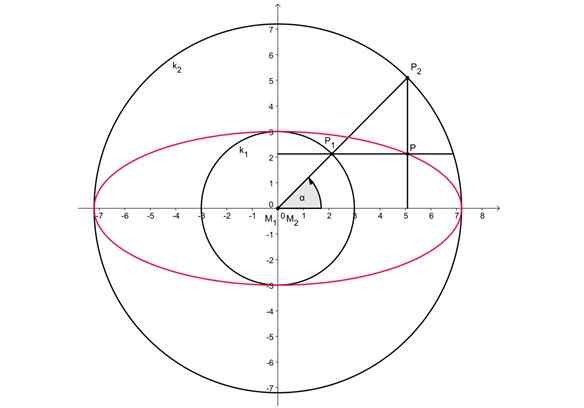Figure 2. Façon de dessiner un ovale à travers deux circonférences concentriques. Source: Wikimedia Commons. Kmhkmh [cc par 3.0 (https: // CreativeCommons.Org / licences / par / 3.0)]

La figure 2, ci-dessus, montre deux circonférences concentriques au centre à l'origine. Le principal axe ovale mesure le même que le diamètre de la circonférence externe, tandis que le plus petit axe correspond au diamètre de la circonférence intérieure.

-Un rayon arbitraire est attiré par la circonférence externe, qui coupe les deux circonférences dans les points P₁ Et P₂.

-Alors le point P est projeté₂ Sur l'axe horizontal.

-D'une manière similaire, le point P est projeté₁ sur l'axe vertical.

-L'intersection des deux lignes de projection est le point P et appartient à l'ovale.

-Tous les points de cette section de l'ovale peuvent être dessinés de cette manière.

-Le reste de l'ovale est dessiné avec la procédure analogue, réalisée dans chaque quadrant.

Exercices

Alors d'autres moyens de construire des ovales seront examinés, étant donné une certaine mesure initiale, qui déterminera sa taille.

- Exercice 1

Dessinez avec une règle et compasse un ovale, connu son principal axe dont la longueur est de 9 cm.

Solution

Dans la figure 3, qui est illustrée ci-dessous, l'ovale résultant apparaît en rouge. Une attention particulière doit être accordée aux lignes pointillées, qui sont les constructions auxiliaires nécessaires pour dessiner un ovale dont le principal axe est spécifié. Nous indiquerons toutes les étapes nécessaires pour atteindre le dessin final.

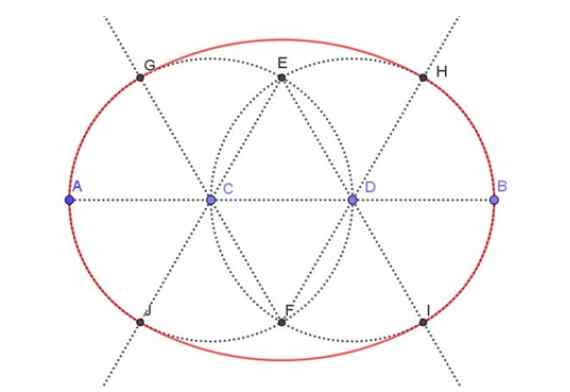figure 3. Construction d'un ovale compte tenu de son axe majeur. Source: F. Zapata.

Étape 1

Dessinez le segment AB de 9 cm avec une règle.

Peut vous servir: Théorème de Bayes

Étape 2

Trisectation du segment AB, c'est-à-dire le divisant en trois segments de longueur égale. Comme le segment AB d'origine mesure 9 cm, les segments AC, CD et DB doivent mesurer 3 cm chacun.

Étape 3

Avec la boussole, la fabrication d'ouverture C et CA attire une circonférence auxiliaire. De même, la circonférence auxiliaire du centre D et de la DB radio est dessinée avec la boussole.

Étape 4

Les intersections des deux circonférences auxiliaires construites à l'étape précédente sont marquées. Nous l'appelons points E et F.

Étape 5

Avec la règle le semi-décrencement suivant.

Étape 6

La semi-sort de l'étape précédente a été coupée aux deux circonférences auxiliaires aux points g, h, i, j respectivement.

Étape 7

Avec la boussole, il est fabriqué au centre en F et avec l'ouverture (ou la radio) FG, l'arc est dessiné GH. De même, faire du centre sur e et avec la radio ei, l'arc est dessiné Ij.

Étape 8

L'union des arches GJ, Ji, Ih et HG Ils forment un ovale dont l'axe principal mesure 9 cm.

Étape 9

Les points et coups auxiliaires sont effacés (masquer).

- Exercice 2

Dessinez avec la règle et la boussole un ovale, dont l'axe mineur est connu et sa mesure est de 6 cm.

Solution

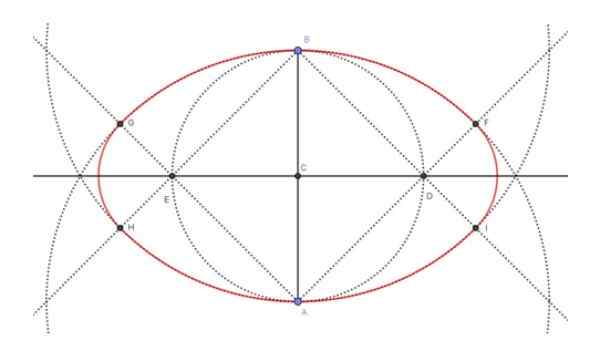Figure 4. Construction d'un ovale compte tenu de son axe mineur. Source: F. Zapata.

La figure ci-dessus (figure 4) montre le résultat final de la construction de l'ovale (en rouge), ainsi que les constructions intermédiaires nécessaires pour l'atteindre. Les étapes qui ont été suivies pour construire l'axe mineur ovale 6 cm étaient les suivantes:

Étape 1

Le segment de 6 cm de long AB est dessiné avec la règle.

Peut vous servir: Théorie des ensembles: caractéristiques, éléments, exemples, exercices

Étape 2

Avec la boussole et la règle, la média est attirée par le segment AB.

Étape 3

L'intersection du MediaTrix avec le segment AB, entraîne le point C du segment AB.

Étape 4

Avec la boussole, la circonférence de Centro C et Radio CA est dessinée.

Étape 5

La circonférence tracée à l'étape précédente intercepte le médiat de l'AB aux points E et D.

Étape 6

Les semi-droits [AD), [AE), [BD) et [BE) sont dessinés.

Étape 7

Avec la boussole, le centre A et la radio AB et le Centro B et Radio BA Radio B et Radio BA sont dessinés.

Étape 8

Les intersections des circonférences dessinées à l'étape 7, avec la semi-sort construite dans l'étape 6, déterminent quatre points, à savoir: f, g, h, i.

Étape 9

Avec le centre-ville en D et Radio di-l'arc si est dessiné. De la même manière, avec E et Radio EG, l'arc GH est dessiné.

Étape 10

L'union de la circonférence arcs fg, gh, hi et si déterminez l'ovale recherché.

Les références

1. En plastique. Courbes techniques: ovale, ovoïde et spirale. Récupéré de: dessiner.Wordpress.com.
2. Mathematische Basteleien. Courbes d'oeufs et ovales. Récupéré de: Mathematische-Basteleien.
3. Université de Valence. Courbes techniques coniques et plates. Récupéré de: OCW.UV.est.
4. Wikipédia. ovale. Récupéré de: est.Wikipédia.org.
5. Wikipédia. ovale. Récupéré de: dans.Wikipédia.org.