Symboles et formules de diamètre, comment le retirer, circonférence

Il diamètre C'est la ligne droite qui passe au centre d'une courbe plate fermée ou d'une figure en deux ou trois dimensions et qui rejoint également ses points opposés. C'est généralement un cercle (une courbe plate), un cercle (une figure plate), une sphère ou un cylindre circulaire droit (objets à trois dimensions).

Bien que la circonférence et le cercle soient généralement considérés comme des synonymes, il y a une différence entre les deux termes. La circonférence est la courbe fermée qui enferme au cercle, qui répond à la condition que la distance entre l'un de ses points et le centre est le même. Cette distance n'est autre que le rayon de la circonférence. Au lieu de cela, le cercle est une figure plate limitée par la circonférence.

Figure 1. Le diamètre des roues à vélo est une caractéristique importante de sa conception. Source: Pixabay.

En cas de circonférence, de cercle et de sphère, le diamètre est un segment droit qui contient au moins trois points: le centre plus deux points du bord de la circonférence ou du cercle, ou la surface de la sphère.

Et quant au cylindre circulaire droit, le diamètre fait référence à la section transversale qui, avec la hauteur, sont ses deux paramètres caractéristiques.

Le diamètre de la circonférence et du cercle, symbolisés par Ø ou simplement la lettre "D" ou "D", est liée à son périmètre, son contour ou sa longueur, qui est indiqué avec la lettre L:

L = π.D = π. soit

Chaque fois que vous avez une circonférence, le quotient entre sa longueur et son diamètre est le nombre irrationnel π = 3.14159 ..., de cette manière:

π = l / d

[TOC]

Comment obtenir le diamètre?

Lorsque le dessin de la circonférence ou du cercle est disponible, ou directement l'objet circulaire, comme une devise ou un anneau par exemple, il est très facile de prendre le diamètre avec une règle. Vous devez simplement vous assurer que le bord de la règle en même temps a deux points de circonférence et le centre de la même.

Peut vous servir: algébrique

Un calibre, Vernier ou King's Foot est très adapté pour mesurer les diamètres externes et internes dans les pièces, les cerceaux, les anneaux, les noix, les tubes et plus.

Figure 2. Vernier numérique mesurant le diamètre d'une pièce. Source: Pixabay.

Si au lieu de l'objet ou de son dessin, vous avez des données comme la radio R, Puis en multipliant par 2, vous avez le diamètre. Et si la longueur ou le périmètre de la circonférence est connu, le diamètre peut également être connu, par autorisation:

D = 2.R
D = l / π

Une autre façon d'obtenir le diamètre est de connaître la zone du cercle, la surface sphérique, la section transversale du cylindre, la zone incurvée de celle-ci ou des volumes de la sphère ou du cylindre. Tout dépend de la figure géométrique. Par exemple, le diamètre est impliqué dans les domaines et volumes suivants:

-Zone de cercle: π.(D / 2)²
-Surface sphérique: 4π.(D / 2)²
-Volume de sphère: (4/3) π.(D / 2)³
-Volume de cylindre circulaire droit: π.(D / 2)².H (H est la hauteur du cylindre)

Figures de constante

Le cercle est une figure plate de constante large, car partout où elle a l'air, la largeur est diamètre D. Cependant, il existe d'autres figures peut-être moins connues dont la largeur est également constante.

Voyons d'abord ce qui est compris par la largeur d'une figure: c'est la distance entre deux lignes parallèles-soupage de support -, qui à leur tour sont perpendiculaires à la direction donnée et qui emprisonne la figure, comme le montre l'image de gauche:

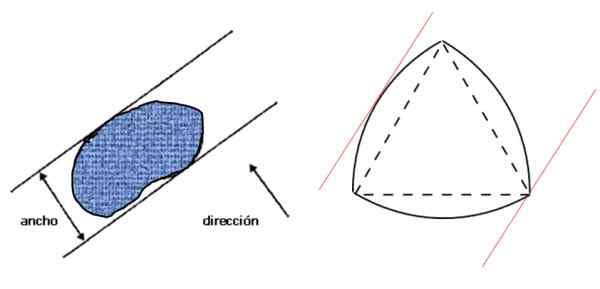figure 3. Largeur de toute figure plate (à gauche) et triangle Reuleaux, une figure large constante (à droite). Source: F. Zapata.

Ensuite, à droite se trouve le triangle Reuleaux, qui est une figure large constante et qui répond à la condition spécifiée dans la figure de gauche. Si la largeur de la figure est D, son périmètre est donné par le théorème de Barbier:

Peut vous servir: mesure approximative des figures amorphes: exemple et exercice

L = π.D

Les égouts de la ville de San Francisco en Californie sont en forme de triangle de Reuleaux, nommé par l'ingénieur allemand Franz Reuleaux (1829 - 1905). De cette façon, les tapas ne peuvent pas tomber dans le trou et dépenser moins de matériau pour les fabriquer, car leur zone est inférieure à celle du cercle:

A = (1- √3).πd² = 0.705.D²

Tandis que pour un cercle:

A = π.(D / 2)² = (π / 4) D²= 0.785.D²

Mais ce triangle n'est pas la seule figure large constante. Les appels peuvent être construits Polygones Reuleaux avec d'autres polygones qui ont un numéro de côtés étranges.

Diamètre d'une circonférence

Dans la figure suivante se trouvent les éléments de la circonférence, définis comme suit:

Corde: segment de ligne qui rejoint deux points de circonférence. Dans la figure est la corde qui rejoint les points C et D, mais les cordes infinies peuvent être tracées qui uniques sont uniques tous les couples de la circonférence.

Diamètre: C'est la corde qui passe par le centre, en joignant deux points de circonférence avec le centre ou. C'est la corde la plus longue d'une circonférence, pour cette raison, elle est appelée "corde majeure".

Radio: segment de ligne qui rejoint le centre avec n'importe quel point de la circonférence. Sa valeur, comme le diamètre, est constante.

Circonférence: C'est l'ensemble de tous les points qui égalisent ou.

Arc: Il est défini comme un segment de circonférence délimité par deux radios (non dessinés sur la figure).

Figure 4. Parties de la circonférence, y compris le diamètre, qui passe par le centre. Source: Wikimedia Commons.

- Exemple 1

Le rectangle montré mesure 10 pouces de hauteur, ce qui, lors de son enroulement, forme un cylindre circulaire droit dont le diamètre est de 5 pouces. Répondre aux questions suivantes:

Il peut vous servir: événements mutuellement exclusifs: propriétés et exemples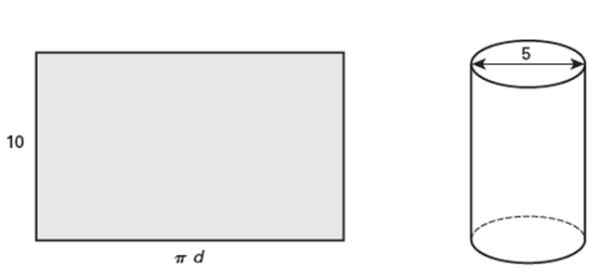Figure 5. Un rectangle roulé devient un cylindre circulaire droit. Source: Jiménez, R. Mathématiques II. Géométrie et trigonométrie. 2e. Édition. Pearson.

a) Quel est le contour du tube?
b) Trouvez la zone rectangulaire
c) Calculer la zone de section transversale du cylindre.

Solution à

Le contour du tube est l = π.D = 5π plg = 15.71 PLG.

Solution B

La zone du rectangle est Base x hauteur, Étant la base L déjà calculée et la hauteur est de 10 plg selon l'énoncé, donc:

A = 15.71 PLG x 10 PLG = 157.1 PLG².

Solution C

Enfin, la zone demandée est calculée comme suit:

A = π.(D / 2)² = (π / 4) D² = (π / 4) x (5 plg)²= 19.63 PLG².

- Exemple 2

Calculez la zone ombrée de la figure 5A. Le carré a le côté L.

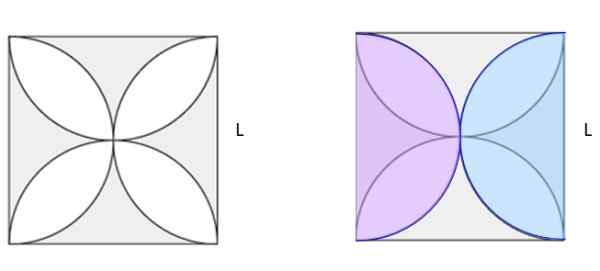Figure 6. Trouvez la zone ombrée dans la figure de gauche. Jiménez, R. Mathématiques II. Géométrie et trigonométrie. 2e. Édition. Pearson.

Solution

Dans la figure 5b, deux demi-cercles identiques de taille dans les couleurs roses et bleus ont été dessinés, superposés à la figure d'origine. Entre eux, ils font un cercle complet. Si le carré du carré est calculé et que la zone du cercle est soustraite, il fait la zone ombrée de la figure 5B. Et l'air bien, il s'avère que c'est la moitié de la zone ombragée en 5A.

-Carré de zone: L²
-Diamètre semi -Circle: L
-Zone de cercle: π.(L / 2)²= (π / 4) L²
-Différence des zones = moitié de la zone ombragée =

L² - (π / 4) L² = [(4 - π) / 4] L²= 0.2146 L²

-Zone ombrée = 2 x 0.2146 L²= 0.4292L2

Combien de diamètres une circonférence a-t-elle?

Des diamètres infinis peuvent être dessinés en cercle, et chacun d'entre eux mesure le même.

Les références

1. Antonio. Triangles de reuleaux et autres courbes de largeur constante. Récupéré de: disseminateurs.com.
2. Baldor, un. 2002. Géométrie plate et espace et trigonométrie. Groupe de patrie culturelle.
3. Jiménez, R. Mathématiques II. Géométrie et trigonométrie. 2e. Édition. Pearson.
4. Wikipédia. Triangle de reuleaux. Récupéré de: c'est.Wikipédia.org.
5. Wolfram Mathworld. Diamètre. Récupéré de: Mathworld.Wolfram.com.