UN rhomboïde C'est une figure plate de quatre côtés, -Un quadrilatère -in que ses côtés et ses angles internes sont différents deux à deux. Par conséquent, le rhomboïde appartient au groupe de parallélogrammes obliques.

Les chiffres géométriques font partie de la nature et en particulier ceux de quatre côtés comme le Rhomboid, ont de nombreuses applications en architecture et en conception.

Figure 1. Les panneaux d'éclairage du stade Allianz Arena à Munich, en Allemagne, s'allument avec les couleurs de l'équipe locale et de la lumière blanche lorsque la sélection de ce pays joue. Source: pxhere.

Nous faisons partie de la façade du stade de football Allianz Arena à Munich. Ce sont des panneaux de rhomboïdes qui s'allument avec les couleurs de l'équipe locale.

C'est donc une figure avec beaucoup de dynamisme visuel, car contrairement à d'autres quadrilatères, il n'a pas d'axe de symétrie. La figure suivante montre divers rhomboïdes avec des orientations variées dans le plan.

Figure 2. Plusieurs rhomboïdes avec différentes orientations dans le plan. Source: F. Zapata.

[TOC]

Caractéristiques des Romboïdes

Ensuite, les principales caractéristiques de cette figure géométrique intéressante:

-Numéro de feuille: 4.

-Nombre de sommets: 4.

-Les côtés opposés sont les mêmes et parallèles, mais les côtés adjacents sont inégaux.

-Il a 4 angles internes: deux aigus (moins de 90 °), désignés par la lettre grecque α et deux obtus (plus de 180 °), appelée β (voir figure 3).

-En ajoutant deux angles contigus du rhomboïde, 180º est obtenu, donc α et β sont donc Supplémentaire.

-La somme des 4 angles internes est égal à 360º.

-Une diagonale est un segment qui commence à partir d'un sommet et se termine au sommet opposé.

-Le point auquel les diagonales de la rhomboïde se croisent est appelée barycenter.

-Les diagonales rhomboïdes ont des tailles différentes.

À propos des diagonales du rhomboïde, il y a des détails importants que nous discuterons ci-dessous.

Peut vous servir: en attente de ligne: formule et équations, représentation, exemples

Diagonales du rhomboïde

Il est très important de souligner que les diagonales des rhomboïdes ne sont pas bisectiques, c'est-à-dire qu'ils ne divisent pas les angles internes de la figure en deux parties égales.

Les diagonales ne sont pas perpendiculaires les unes aux autres. Cependant, nous pouvons facilement les calculer avec le théorème du cosinus. Ainsi, la principale diagonale D_M Dans le rhomboïde de la figure 3 est:

D_M = √ (a² + b² - 2.UN B.cos β)

Et la diagonale mineure D_m serieuse:

D_m = √ (a² + b² - 2.UN B.cos α)

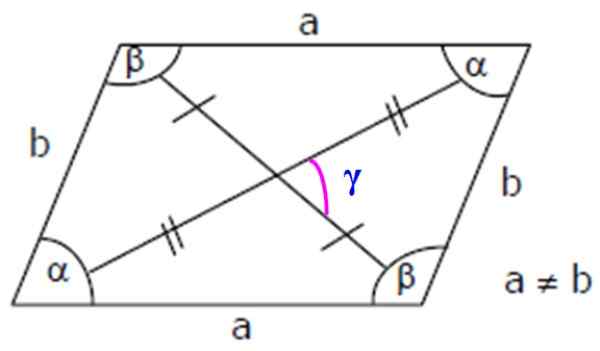figure 3. Éléments habites: côtés, angles internes et diagonaux. Source: Wikimedia Commons.

Important: Comme α et β sont supplémentaires, il est accompli que:

sin α = sin β

cos α = -cos β

Ces propriétés des raisons trigonométriques doivent être prises en compte lors de la résolution des exercices.

Comment éliminer le périmètre et la zone

Pour trouver le périmètre et la zone que nous donnerons le nom des côtés du rhomboïde, ce sera pour et b. Nous avons également la hauteur du rhomboïde, appelé H, qui est la ligne tracée de l'un des sommets et dirigée perpendiculairement du côté opposé de la figure.

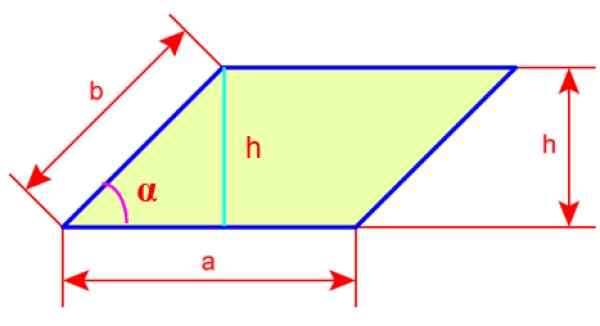Figure 4. Côtés et hauteur de rhomboïdes. Source: Wikimedia Commons.

Périmètre du rhomboïde

Le périmètre du rhomboïde est calculé en ajoutant les longueurs de ses quatre côtés. Appelons P au périmètre, alors:

P = 2a + 2b

Nous pouvons également l'exprimer à travers:

P = 2 (a + b)

Périmètre connaissant la hauteur

Si nous regardons bien, la hauteur H peut être déterminée à partir du triangle à gauche sur la figure 4. Le côté B serait l'hypoténuse et la hauteur h le cateto opposé à l'angle α, donc:

sin α = opposé / Hypotenusa cateto

Ou bien:

sin α = h / b

Ensuite, nous nettoyons B:

b = h / sin α

Nous remplaçons dans le périmètre P:

P = 2 [a + (h / sin α)]

Zone habituelle

La zone rhomboïde est la mesure de sa surface. Et comme il s'agit d'un parallélogramme, sa zone A est donnée par l'expression bien connue:

Peut vous servir: facteur commun pour le regroupement des termes: exemples, exercices

A = hauteur de base x

Que selon les figures 3 et 4, il s'exprime à travers:

A = a x h

Zone connaissant les deux côtés et un angle interne

En appliquant la trigonométrie de base de la section précédente, nous trouvons des expressions équivalentes pour la zone des rhomboïdes:

h = b. Sin α

Ensuite, la zone est comme ceci:

A = a. b. Sin α

Se souvenir de ce que nous avons dit ci-dessus sur les angles supplémentaires, nous pouvons remplacer Sen α par Sen β si nécessaire.

Zone connaissant les diagonales et l'angle entre eux

Enfin, si nous connaissons les diagonales D_M et d_m, plus l'angle γ entre eux (voir figure 3), la zone peut être calculée par le semi-produit des diagonales à travers le sein dudit angle:

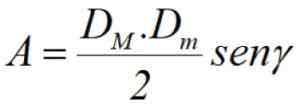
Exercice résolu

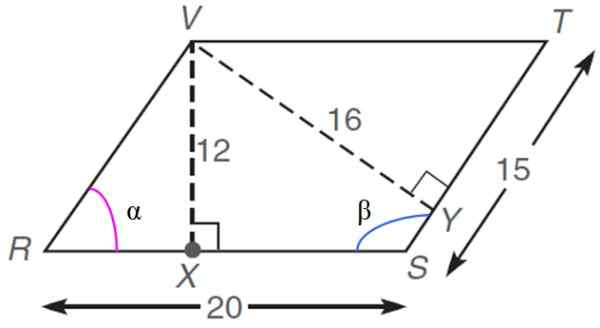
Dans le rhomboïde suivant, dont les dimensions sont données dans des unités arbitraires ou.pour., trouver:

a) La valeur du périmètre

b) la zone

c) angles internes α et β

d) la longueur du segment Rx

e) la mesure de chacune des diagonales

Solution à

Le périmètre P est:

P = 2 (a + b)

Nous identifions d'abord les valeurs de A et B:

A = 20

B = 15

Nous remplaçons la formule et calculons:

P = 2. (20 + 15) = 70 u.pour.

Solution B

Le diagramme fournit la hauteur h = 12 u.A, par conséquent, la zone peut être calculée avec la formule:

A = a x h

A = 20 x 12 u.pour.² = 240 u.pour.²

Quelle que soit l'unité sélectionnée pour mesurer les côtés et la hauteur, la zone est toujours exprimée en unités carrées.

Le même résultat si vous obtenez lors du calcul de la zone avec l'autre hauteur du rhomboïde, qui vaut 16 U.pour. En effet:

A = 16 x 15 u.pour.² = 240 u.pour.²

Solution C

L'angle α peut être calculé à travers:

Il peut vous servir: mesures de position, tendance centrale et dispersion

h = b. Sin α

Car les valeurs H et B sont donc connues:

α = arcsen (h / b) = arcsen (12/15) = 53.13e

Rappelant que les angles α et β sont supplémentaires, il est rempli:

α + β = 180º ⇒ β = 180 - 53.13e = 126.87º

Solution d

La longueur du segment RX est facilement calculée, car il y a suffisamment d'informations pour les trouver. Par exemple à travers:

Rx = RV . cos α = 15 . COS 53.13e u.pour. = 9 u.pour.

Aussi à travers le théorème de Pythagore à travers le triangle rectangle des côtés 15 et 12 u.pour:

(RV)² = (Rx)² + H²

Effacer la durée du segment des intérêts:

Rx = √ [(RV)² - H²] = √ [15² - 12²] = √81 = 9

Solution E

La mesure de l'une des diagonales, par exemple la diagonale qui rejoint les sommets R et T, qui est une diagonale majeure, est donnée par le théorème de cosinus, comme expliqué précédemment, nous remplacez donc les valeurs: là-bas:

D_M = √ (20² + 25² - 2. vingt. quinze .Cos 126.87º) = 37.22 u.pour.

Pour la diagonale mineure:

D_m = √ (20² + 25² - 2. vingt. quinze .COS 53.13e) = 25.79 u.pour.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Baldor, un. 1973. Géométrie et trigonométrie. Éditorial culturel d'Amérique centrale.
3. ET. POUR. 2003. Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
4. Jiménez, R. 2010. Mathématiques II. Géométrie et trigonométrie. Deuxième édition. Prentice Hall.
5. Polygones réguliers. Récupéré de: mec.ingénierie.USAC.Édu.GT.
6. Formules d'univers. Rhomboïde. Récupéré de: universoformules.com.
7. Wikipédia. Rhomboïde. Récupéré de: est.Wikipédia.org.