Caractéristiques du triangle Balacket, propriétés, formules, zone

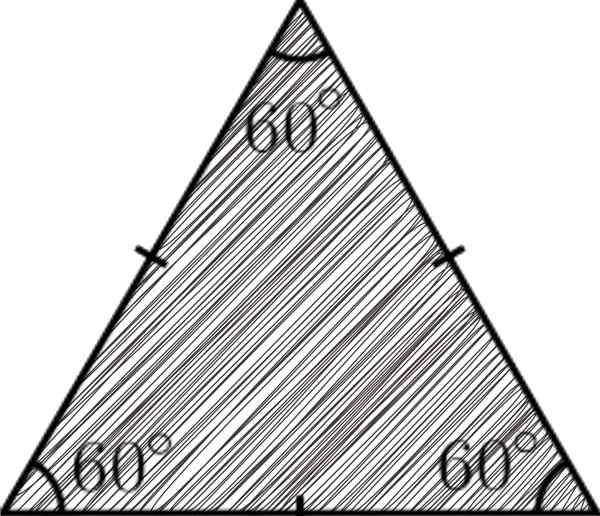
UN triangle équilatéral C'est un polygone à trois faces, où tous sont les mêmes; c'est-à-dire qu'ils ont la même mesure. Pour cette caractéristique, il a reçu le nom d'équilatéral (côtés égaux).

Les triangles sont des polygones considérés comme les plus simples en géométrie, car trois côtés, trois angles et trois sommets se forment. Dans le cas du triangle équilatéral, pour avoir des côtés égaux, il implique que ses trois angles seront également.

Un exemple du triangle équilatéral

[TOC]

Caractéristiques des triangles d'équilibre

- Côtés égaux

Les triangles équilatéraux sont des figures plates et fermées, composées de trois lignes de lignes. Les triangles sont classés par leurs caractéristiques, par rapport à leurs côtés et à leurs angles; L'équilatéral a été classé en utilisant la mesure de leurs côtés comme paramètre, car ce sont exactement les mêmes, c'est-à-dire qu'ils sont congrus.

Le triangle équilatéral est un cas particulier du triangle isocèle car deux de ses côtés sont congruents. C'est pourquoi tous les triangles équilatéraux sont également isocèles, mais tous les triangles isoscéles ne seront pas équilatéraux.

De cette façon, les triangles équilatéraux ont les mêmes propriétés d'un triangle isocèle.

Les triangles équilatéraux peuvent également être classés par l'amplitude de leurs angles internes comme un triangle aigu équilatéral, qui a les trois côtés et les trois angles internes avec la même mesure. Les angles seront aigus, c'est-à-dire qu'ils seront inférieurs à 90^soit.

- Composants

Les triangles en général ont plusieurs lignes et points qui le composent. Ils sont utilisés pour calculer la zone, les côtés, les angles, la médiane, la bissectrice, la média et la hauteur.

• La médiane: C'est une ligne qui part du point médian d'un côté et atteint le sommet opposé. Les trois médiums assistent à un point appelé baricentro ou centroïde.
• La bissectrice: C'est un semi-droit qui divise l'angle des sommets en deux angles de mesure égale, il est donc appelé axe de symétrie. Le triangle équilatéral a trois axes de symétrie. Dans le triangle équilatéral, la bissectrice est tirée du sommet d'un angle par rapport à son côté opposé, le coupant en milieu médian. Vous êtes à point appelé incitateur.
• Le MediaTrix: C'est un segment perpendiculaire au côté du triangle qui provient au milieu de ce. Il y a trois médias dans un triangle et ils sont d'accord à un point appelé circoncentro.
• L'hauteur: C'est la ligne qui va du sommet au côté qui est opposé et que cette ligne est perpendiculaire à ce côté. Tous les triangles ont trois hauteurs qui coïncident à un point appelé OrtoSenter.

Dans le graphique suivant, nous observons un triangle scalène où certains des composants susmentionnés sont détaillés

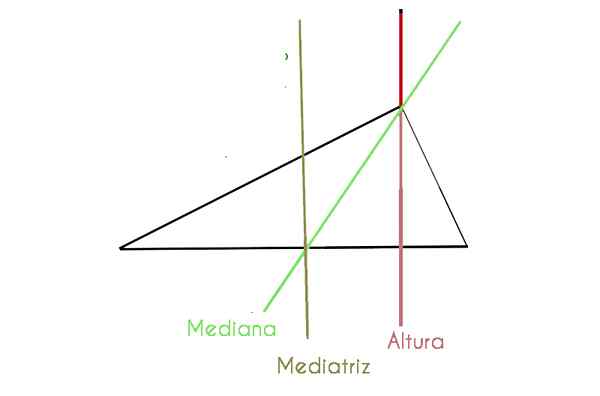Nous pouvons clairement voir les composants, quelque chose qui est plus difficile dans le triangle équilatéral, car certains coïncident. Nous les expliquons ci-dessous:

La bissectrice, la médiane et la média sont une coïncidence

La bissectrice se divise à côté d'un triangle en deux parties. Dans les triangles équilatéraux, ce côté sera divisé en deux exactement les mêmes parties, c'est-à-dire que le triangle sera divisé en deux triangles de rectangles congruents.

Ainsi, la bissectrice tirée de n'importe quel angle d'un triangle équilatéral coïncide avec la médiane et le médiat du côté opposé à cet angle.

Peut vous servir: Relations de proportionnalité: concept, exemples et exercices

Exemple:

La figure suivante montre le triangle ABC avec un M-D qui divise l'un de ses côtés en deux segments AD et BD.

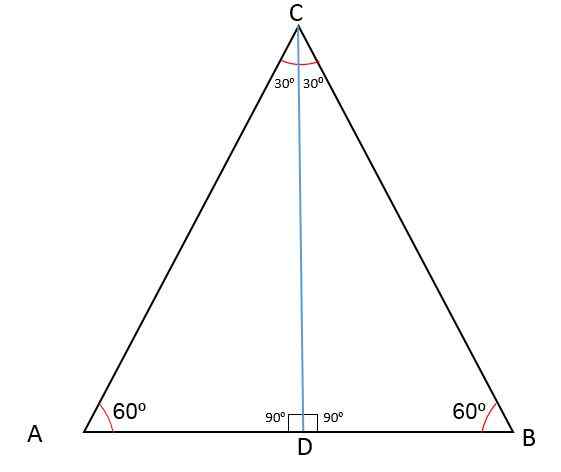
Lors du dessin d'une ligne du point D au sommet opposé, par définition, le CD médian est obtenu, qui est relatif au sommet C et sur le côté AB.

Comme le segment CD divise le triangle ABC en deux triangles CDB et CDA égaux, cela signifie que ce sera le cas de la congruence: côté, angle, côté et donc CD sera également le BCD BIsectoral.

Lors du dessin du segment CD, l'angle de sommet est divisé en deux angles égaux de 30^soit, L'angle du sommet A continue de mesurer 60^soit Et la ligne de CD forme un angle de 90^soit Concernant le point médian D.

Le segment CD forme des angles qui ont la même mesure pour les triangles ADC et BDC, c'est-à-dire qu'ils sont supplémentaires de telle manière que la mesure de chacun soit:

Médicament. (ADB) + Med. (ADC) = 180^soit

2 _* Médicament. (ADC) = 180^soit

Médicament. (ADC) = 180^soit ÷ 2

Médicament. (ADC) = 90^soit.

Et donc, le segment de CD est également le média du côté AB.

La bissectrice et la hauteur sont coïncidentes

Lorsque la bissector trace du sommet d'un angle au milieu du côté opposé, cela divise le triangle équilatéral en deux triangles congruents.

De telle manière qu'un angle de 90 se forme^soit (droit). Cela indique que ce segment de ligne est totalement perpendiculaire à ce côté, et par définition cette ligne serait la hauteur.

De cette façon, la bissectrice de tout angle d'un triangle équilatéral, coïncide avec la hauteur par rapport au côté opposé de cet angle.

Orocentro, Baricentro, Incentro et Colecentro Coinside

Comme la hauteur, la médiane, la bissectrice et le média sont représentées en même temps par le même segment, dans un triangle équilatéral, les points de rencontre de ces segments - l'orthocentre, le barcentrique, l'incenteur et la circulation - se trouvent au même point:

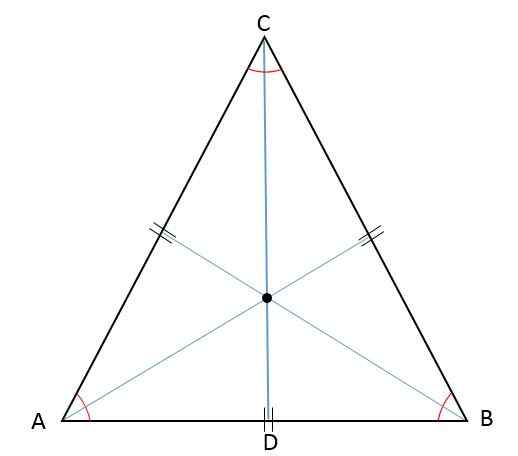
Propriétés

La principale propriété des triangles équilatéraux est qu'ils seront toujours des triangles isocèles, car les isocèles sont formés par deux côtés congruents et les équilibre.

De cette façon, les triangles équilatéraux ont hérité de toutes les propriétés du triangle isocèle:

Angles internes

La somme des angles internes est toujours égal à 180^soit, Et puisque tous ses angles sont congruents, chacun d'eux mesurera 60^soit.

Angles externes

La somme des angles externes sera toujours égal à 360^soit, Par conséquent, chaque angle externe mesurera 120^soit. C'est parce que les angles internes et externes sont supplémentaires, c'est-à-dire en les ajoutant, ils seront toujours égaux à 180^soit.

Somme des côtés

La somme des mesures de deux côtés doit toujours être supérieure à la mesure du troisième côté, c'est-à-dire A + B> C, où A, B et C sont les mesures de chaque côté.

Côtés congruents

Les triangles équilatéraux ont leurs trois côtés avec la même mesure ou la même longueur; c'est-à-dire qu'ils sont congruents. Par conséquent, dans l'élément précédent, vous devez = b = c.

Angles congruents

Les triangles équilatéraux sont également connus sous le nom de triangles équilibrés, car leurs trois angles internes sont conformes les uns aux autres. C'est parce que tous leurs côtés ont également la même mesure.

Il peut vous servir: variable nominale: concept et exemples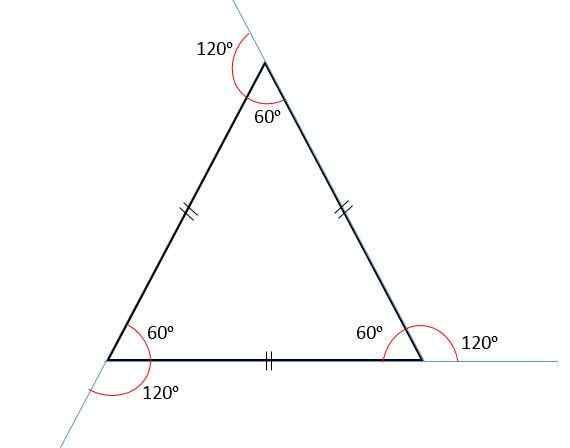

Comment calculer le périmètre?

Le périmètre d'un polygone est calculé par la somme des côtés. Comme dans ce cas, le triangle équilatéral a tous ses côtés avec la même mesure, son périmètre est calculé avec la formule suivante:

P = 3 _* côté.

Comment calculer la hauteur?

Comme la hauteur est la ligne perpendiculaire à la base, la divise en deux parties égales en s'étendant au sommet opposé. Ainsi, deux triangles se forment des rectangles égaux.

La hauteur (H) représente le Cateto inverse (A), la moitié du côté AC à la Cateto (B) adjacente et le côté BC représente l'hypoténuse (C).

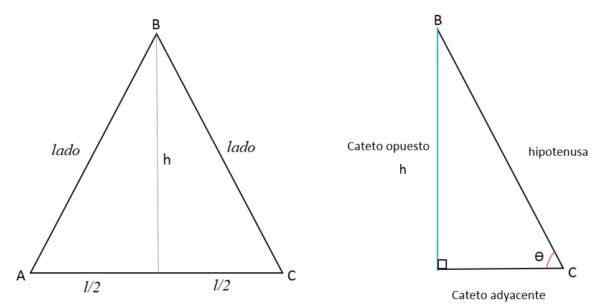
À l'aide du théorème de Pythagore, la valeur de la hauteur peut être déterminée:

pour² + b² = C²

Où:

pour² = hauteur (h).

b² = côté b / 2.

c² = côté a.

Remplacer ces valeurs dans le théorème de Pythagore et effacer la hauteur que vous avez:

H² + ( l / 2)² = l²

H² +  l²/ / 4 = l²

H² = l²  -  l²/ / 4

H² = (4_*l² -  l²) / / 4

H² =  3_*l² / /4

√H² = √ (3_*l² / /4)

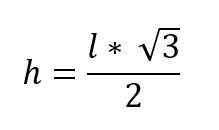
Si l'angle formé par les côtés congruents, la hauteur (représentée par une jambe) est connue, elle peut être calculée en appliquant les raisons trigonométriques.

Les catégories sont appelées opposées ou adjacentes en fonction de l'angle qui est pris comme référence.

Par exemple, dans la figure précédente, le Cateto H sera opposé à l'angle C, mais adjacent à l'angle b:

Ainsi, la hauteur peut être calculée avec:

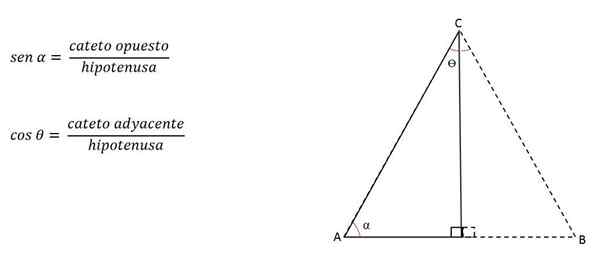
Comment calculer les côtés?

Il y a des cas où les mesures des côtés du triangle ne sont pas connues, mais sa hauteur et les angles qui se forment dans les sommets.

Pour déterminer la zone dans ces cas, il est nécessaire d'appliquer des raisons trigonométriques.

Connaissant l'angle de l'un de ses sommets, la catégorie est identifiée et la raison trigonométrique correspondante est utilisée:

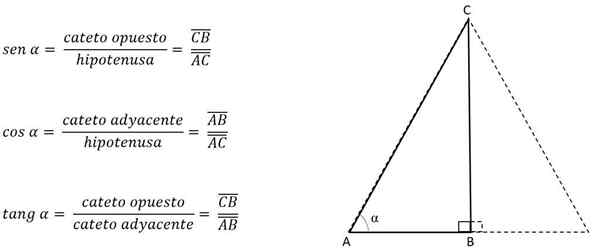
Ainsi, le Cateto AB sera opposé à l'angle C, mais adjacent à l'angle a. Selon le côté ou la jambe correspondant à la hauteur, l'autre côté est éliminé pour obtenir la valeur de cela, sachant que dans un triangle équilatéral, les trois côtés auront toujours la même mesure.

Comment calculer la zone?

Les triangles sont toujours calculés avec la même formule, multipliant la base par hauteur et divisant par deux:

Zone = (b _* H) ÷ 2

Sachant que la hauteur est donnée par la formule:

Exercices

- Premier exercice

Les côtés d'un triangle équilatéral ABC mesurent 20 cm chacun. Calculez la hauteur et la zone de ce polygone.

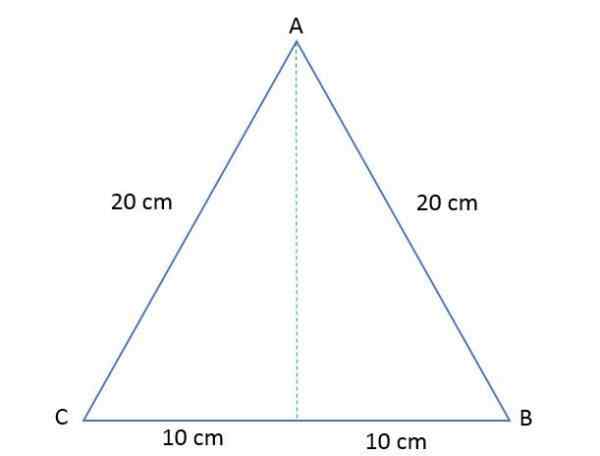
Solution

Pour déterminer l'aire de ce triangle équilatéral, il est nécessaire de calculer la hauteur, sachant qu'en le dessinant, il divise le triangle en deux rectangles égaux.

De cette façon, vous pouvez utiliser le théorème de Pythagore pour le trouver:

pour² + b² = C²

Où:

A = 20/2 = 10 cm.

B = hauteur.

C = 20 cm.

Les données sont remplacées dans le théorème:

dix² + b² = 20²

100 cm + b² = 400 cm

b² = (400 - 100) cm

b² = 300 cm

B = √300 cm

B = 17,32 cm.

C'est-à-dire que la hauteur du triangle est égale à 17,32 cm. Maintenant, il est possible de calculer la zone de triangle donnée en remplaçant la formule:

Zone = (b _* H) ÷ 2

Zone = (20 cm _* 17,32 cm) ÷ 2

Il peut vous servir: transformations linéaires: propriétés, quels sont les types, les types, les exemples

Zone = 346,40 cm² ÷ 2

Zone = 173,20 cm².

Une autre façon plus simple de résoudre l'exercice consiste à remplacer les données dans la formule directe de la zone, où la valeur de la hauteur est également implicitement trouvée:

- Deuxième exercice

Dans un champ qui a la forme d'un triangle équilatéral, les fleurs vont planter. Si le périmètre de ce terrain est égal à 450 m, calculez le nombre de mètres qui occupaient les fleurs.

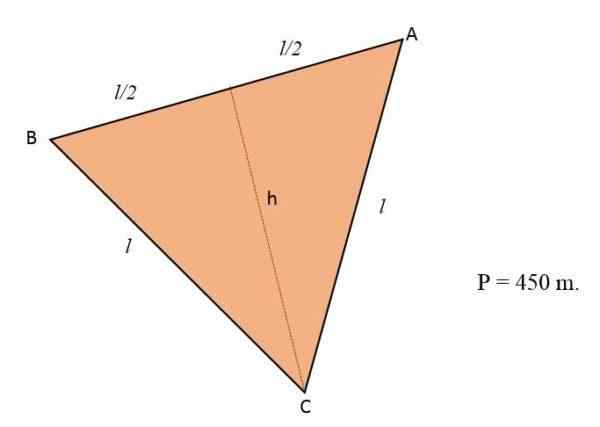
Solution

Sachant que le périmètre d'un triangle correspond à la somme de ses trois côtés et que le terrain est en forme de triangle équilatéral, les trois côtés de cela auront la même mesure ou la même longueur:

P = côté + côté + côté = 3 _* l

3 _* l = 450 m.

L = 450 m ÷ 3

L = 150 m.

Maintenant, il est nécessaire de calculer la hauteur de ce triangle.

La hauteur divise le triangle en deux triangles de rectangles congruents, où l'une des catégories représente la hauteur et l'autre moitié de la base. Par le théorème de Pythagore, la hauteur peut être déterminée:

pour² + b² = C²

Où:

pour = 150 m ÷ 2 = 75 m.

c = 150 m.

b = hauteur

Les données sont remplacées dans le théorème:

(75 m)² + b² = (150 m)²

5.625 m + b² = 22.500 m

b² = 22.500 m - 5.625 m

b² = 16.875 m

b = √16.875 m

b = 129,90 m.

Ainsi, la zone que les fleurs occuperont seront:

Zone = b * h ÷ 2

Zone = (150 m _* 129,9 m) ÷ 2

Zone = (19.485 m²) ÷ 2

Zone = 9.742,5 m²

- Troisième exercice

Le triangle équilatéral ABC est divisé par un segment de ligne qui va de son sommet C au point médian D, situé du côté opposé (AB). Ce segment mesure 62 mètres. Calculez la zone et le périmètre de ce triangle équilatéral.

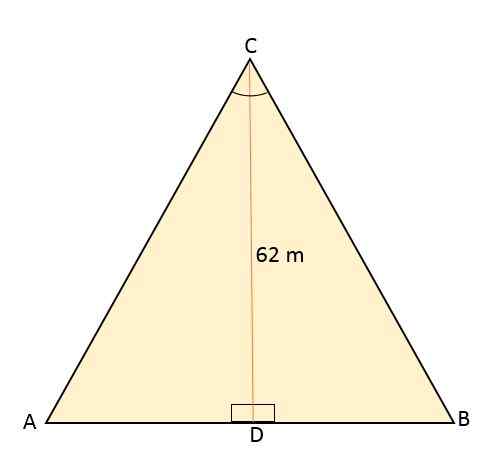
Solution

Sachant que le triangle équilatéral est divisé par un segment de ligne qui correspond à la hauteur, formant ainsi deux rectangles congruents, cela divise également l'angle de sommet C en deux angles avec la même mesure, 30^soit chacun.

La hauteur forme un angle de 90^soit Par rapport au segment AB, et l'angle du sommet pour ensuite mesurer 60^soit.

Puis en utilisant l'angle de 30 comme référence^soit, La hauteur du CD est établie en tant que cateto adjacent à l'angle et à la Colombie-Britannique comme hypotenusa.

À partir de ces données, la valeur de l'un des côtés du triangle peut être déterminée, en utilisant les raisons trigonométriques:

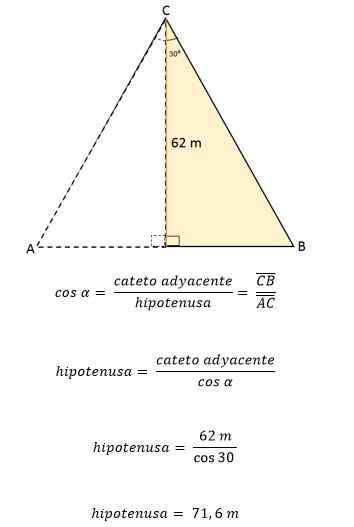
Comme dans le triangle équilatéral, tous les côtés ont exactement la même mesure ou la même longueur, cela signifie que chaque côté du triangle équilatéral ABC est égal à 71,6 mètres. Sachant cela, il est possible de déterminer votre région:

Zone = b * h ÷ 2

Zone = (71,6 m _* 62 m) ÷ 2

Zone = 4.438,6 m² ÷ 2

Zone = 2.219.3 m²

Le périmètre est donné par la somme de ses trois côtés:

P = côté + côté + côté = 3 _* l

P = 3_*l

P = 3 _* 71,6 m

P = 214,8 m.

Les références

1. Álvaro Rendón, à. R. (2004). Dessin technique: cahier d'activité.
2. Arthur Goodman, L. H. ( mille neuf cent quatre vingt seize). Algèbre et trigonométrie avec géométrie analytique. Pearson Education.
3. Baldor, un. (1941). Algèbre. Havane: culture.
4. Barbosa, J. L. (2006). Géométrie euclidienne plate. SBM. Rio de Janeiro, .
5. Coxford, un. (1971). Géométrie une approche de transformation. États-Unis: Laidlaw Brothers.
6. Euclide, R. P. (1886). Éléments de géométrie d'Euclide.
7. Héctor Trejo, J. S. (2006). Géométrie et trigonométrie.
8. León Fernández, G. S. (2007). Géométrie intégrée. Institut technologique métropolitain.
9. Sullivan, J. (2006). Algèbre et trigonométrie. Pearson Education.