Tidecágono

Figure 1.- À gauche un tridecácágone régulier et à droite, une monnaie de 20 couronnes de la République tchèque, avec un contour en forme de bridecagon inscrit dans une circonférence, d'une part, il a le lion de bohème et de l'autre à San Wenceslao, Patron, patron de la République tchèque, montée à cheval. Source: F. Zapata.

Qu'est-ce qu'un tridecágono?

Le tridecagon est une figure géométrique plate de la famille des polygones et qui se caractérise par 13 côtés et 13 sommets. Un autre nom pour ce polygone est Triskaidecágono, Nombre dérivé du grec.

Les 13 côtés sont des segments de ligne qui enfin près pour façonner la figure. Les polygones, qui sont nommés selon la quantité de côtés, sont une riche source d'inspiration pour l'architecture, la construction et la conception de nombreux objets, à la fois l'art et les utititaires.

Propriétés de Tridecágono

Le Tridecágono partage avec les autres polygones les caractéristiques et propriétés suivantes:

-Côtés, Ce sont les segments de ligne qui sont joints pour former la figure, qui dans le cas du tridecágono est 13. Ils sont identifiés par des lettres minuscules.

-Sommets, C'est ainsi que les points d'intersection des côtés consécutifs sont appelés et désignent généralement avec des majuscules. Le tridecágono a 13 sommets.

-Périmètre, équivalent à la somme des côtés. Si tous les côtés ont une mesure égale «A», le périmètre est simplement 13 × A, mais si les côtés sont inégaux, le périmètre ajoute chacune des longueurs des côtés.

-centre, C'est le point qui maintient la même distance avec les sommets et les côtés.

-Diagonale, Une ligne qui rejoint un sommet à un autre sommet non consécutif (les sommets consécutifs sont unis par les côtés).

-Angles internes, Ils sont formés entre deux côtés adjacents de la figure et sur la partie intérieure du polygone, et son sommet est le sommet commun aux deux côtés.

Peut vous servir: milétus tel théorème

-Angles externes, Ils sont à l'extérieur du polygone, entre un côté et la prolongation de l'un des côtés consécutifs jusqu'au premier.

-Radio, Distance à distance Vertix du tridecágon.

-Angle central, C'est celui dont le sommet est le centre du polygone.

-Apothème, segment qui rejoint le centre d'un côté avec le centre de la figure et forme 90º de ce côté.

Thunder régulier et irrégulier

Threecarons peut être:

-Régulier, Lorsque la mesure de tous ses treize côtés est la même et que ses angles internes mesurent le même.

-Irrégulier, Si un ou plusieurs côtés ont des mesures différentes.

Dans le cas du tridecácágone ordinaire, les formules suivantes peuvent être appliquées:

Angle interne

Pour un polygone ordinaire, la formule qui permet de calculer la valeur de l'angle interne est:

Où n représente le nombre de côtés, qui dans ce cas est 13. Avec cette valeur, c'est:

I = (11 × 180º) / 13 ≈ 152.3e

Diagonales

Le nombre de diagonales est calculé par la formule suivante, même valide si le polygone est irrégulier:

Pour n = 13 résultats:

D = 13 × 10/2 = 65 diagonales

Apothème

La valeur de l'apothème l_POUR  Il est calculé avec la formule suivante, étant "une" la longueur du côté:

L_POUR ≅ 2.0286a

Zone

Si le périmètre P et la longueur de l'apothème L_POUR, La région de Tridecágono est calculée par:

A = (p × l_POUR) / 2

Selon le côté «A», la formule reste:

A = (13a × l_POUR) / 2

Remplacement de la mesure_POUR De la section précédente, une formule pour la zone qui ne dépend que de la longueur du côté est obtenue:

A = (13a × 2.0286a) / 2 ≈ 13.186a²

Peut vous servir: Distribution hypergéométrique: formules, équations, modèle

Exercer

Si le diamètre d'une couronne de 20 mm est de 26 mm, combien coûtent le côté et la zone du tridecágono enregistré dans le cercle de la monnaie?

Solution

De la figure, il y a un triangle rectangulaire, dont les catégories sont l'apothème et la moitié de la longueur du côté, avec l'hypotenusa égal au rayon de la monnaie, qui est la moitié du diamètre. Comme cela vaut 26 mm, la radio R est égale à 13 mm.

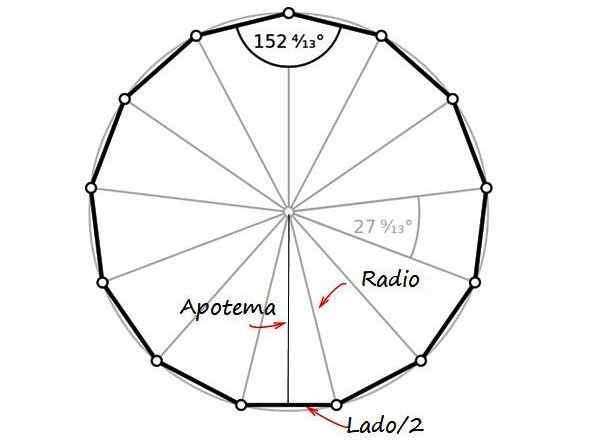Figure 2. La radio, l'apothéme et la moitié du côté du trindecagon forment un triangle rectangle. Source: Wikimedia Commons / F. Zapata.

Par Pythagore Theorème:

Depuis L_POUR ≈ 2.0286a, vous avez:

R² = (2.0286a)² + (0.5e)² = 4.3652A²

Le côté est:

Avec cette valeur, la zone de la monnaie est:

A ≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

Le lecteur est laissé à comparer ce résultat avec la zone obtenue en supposant que la monnaie est circulaire de rayon r = 13 mm.

Comment est un tridecágono?

Le Trindecagon ordinaire est des polygones qui n'admettent pas la construction exacte en utilisant uniquement la règle et la boussole, c'est-à-dire que ce n'est pas un polygone à constructeur. Ils ne sont que construisibles, au moins en théorie, les polygones dont le nombre de côtés ne comprend que des facteurs premiers de la forme:

Les nombres premiers de cette façon sont appelés Cousins ​​fermat, Mais le numéro 13, bien qu'il soit cousin, n'a pas cette forme.

Cependant, vous pouvez dessiner un trindecagon ordinaire qui est enregistré dans une circonférence, chaque sommet a l'intersection avec, sans être remarqué à l'œil nu. Pour cela, c'est nécessaire.

Peut vous servir: triangle obtusangle

Une façon de construire un tridecácágone régulier, bien que pas le seul, consiste à dessiner les coups comme indiqué dans l'animation suivante:

figure 3. Construction d'un tridecagon ordinaire. Source: Wikimedia Commons.

Et cette autre animation décrit également comment faire un tridecágono approximativement, avec une règle et une boussole:

Figure 4.- Moyen alternatif de construire un tridecagon approximativement régulier avec une règle et une boussole. Source: Wikimedia Commons.

Exemples de tridecágel

CONCAVE ET CONVEX TUNDER

Lorsque les angles internes du tridecágono sont inférieurs à 180 °, la figure est convexe, tandis que si un ou plusieurs angles internes sont supérieurs à 180 °, alors le tridecágono est concave.

Le tridecácágon régulier est convexe, car ses angles internes mesurent environ 152.3e chacun.

Utilisation de Tridecágono dans Numismatics

Couronne tchèque

Numismatics est la science des pièces de monnaie, des médailles, des billets et des puces. Les polygones sur de nombreux côtés sont idéaux comme éléments décoratifs dans la conception des pièces, en particulier celles qui ont de nombreux côtés, comme le tridecágono.

Toutes les pièces ne sont pas rondes, cependant, les polygones sur de nombreux côtés ressemblent à la forme circulaire, plus il a de côtés, plus l'approche est grande. Par conséquent, les concepteurs de pièces utilisent les polygones de nombreux côtés pour introduire une touche d'originalité dans leur conception.

Divers polygones sont utilisés à cet effet, comme la monnaie supérieure, appelée la couronne et de la République tchèque, un bon exemple de l'utilisation de Tridecágono comme élément de conception.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Dessin. Polygones réguliers. Récupéré de: dessin.com.
3. Hartley, M. Construire un tridecagon. Récupéré de: youtube.com
4. Wikipédia. Polygone constructible. Récupéré de: est.Wikipédia.org.
5. Wikiwand. Mamecagon. Récupéré de: wikiwand.com.