Toroïde ou Toro Dona

Nous expliquons ce qu'est un taureau ou un taureau, ses caractéristiques, son volume, sa surface, les applications et montrons plusieurs exemples

Qu'est-ce qu'un toroïde?

Il Toroïde C'est un corps géométrique à trois dimensions sous la forme d'un cerceau, d'un anneau, d'un beignet ou d'un beignet, d'où le nom de "Toro Dona", appartenant à la classe d'objets appelés Solides de la révolution.

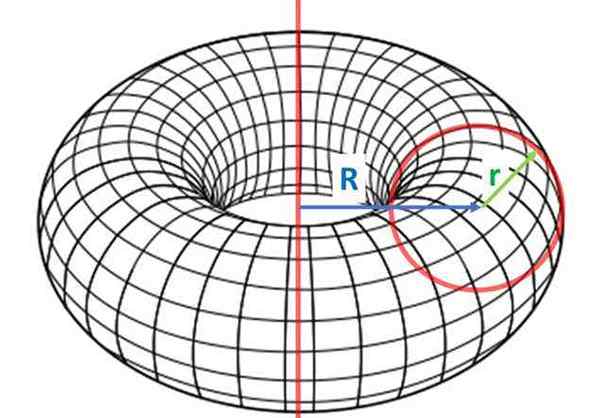
Un toroïde est généré en tournant une figure plate fermée, autour d'une ligne appartenant au même plan de la figure, mais ne l'intercepte pas, comme indiqué ci-dessous:

Un taureau, qui est une surface de révolution qui est obtenue en tournant une figure plate fermée (comme circonférence) autour d'un axe fixe. Source: Wikimedia Commons

La principale caractéristique du Toroïde est que, bien qu'il s'agisse d'une surface fermée, elle a un trou. Cela signifie que deux points de sa surface peuvent être connectés par un segment qui est en dehors de l'objet.

Une autre caractéristique du Toroïde est qu'il s'agit d'une figure à trois dimensions sans sommet. Cette caractéristique le partage avec d'autres corps volumétriques tels que la sphère, mais alors que la sphère est une surface convexe, le taureau est simultanément concave et convexe.

Parmi les taureaux, le taureau C'est le plus courant et est obtenu à partir de la rotation d'un cercle radio r, Concernant un axe de distance R du premier. La radio R (en minuscules) est connue sous le nom de rayon mineur et R (capital) est le plus grand rayon.

Volume d'un toroïde

Un taureau est généré en tournant une figure plate fermée de la zone POUR autour d'un axe de rotation qui ne le coupe pas. Indiquer R La distance entre l'axe et le centroïde de la figure plate, le volume du taureau de la révolution est:

Peut vous servir: fonctions trigonométriques inverses: valeur, dérivés, exemples, exercices

V = 2πr⋅ a 

Ce résultat est obtenu lors de l'application du Théorème de Pappus Pour le volume d'un solide de révolution, qui indique que le volume de toute révolution solide est obtenu en multipliant la zone de la figure qui est brisée par le périmètre de la circonférence formée par la rotation du centroïde (ou centre de gravité ) de la figure tournée, autour de l'axe de rotation.

Volume d'un taureau

Le taureau est le toroïde généré par un cercle radio r. Si la distance de l'axe de rotation au centre du cercle tourné est R, il est alors nécessaire de volumer le taureau est:

V = (2πr) ⋅ (πr²) = 2π²R³

Surface d'un taureau

Être une figure plate simplement liée POUR et contour L. Si une telle figure est tournée autour d'un axe contenu dans le même plan de la figure, mais qui ne le traverse pas, alors la surface générée est une zone de taureau:

S = 2πr⋅ L

Étant r à la distance de l'axe au centre de gravité ou de centroïde, de la figure Generatrix.

Ce résultat est une conséquence de Théorème de Pappus Pour la surface d'une révolution solide.

Surface d'un taureau

Le taureau circulaire de section croisée de Radio R (minuscules) et le maire de radio R (majuscules) est un taureau particulier appelé Toro.

Comme le contour l d'un cercle de rayon r est 2πr, Ensuite, la zone de la surface dudit taureau est:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Applications toroïdes

En raison de ses caractéristiques géométriques, le taureau a d'innombrables applications pratiques et culturelles. Pour commencer, les cerceaux ou les anneaux sont des pièces toroïdales qui ont diverses utilisations:

Peut vous servir: carrés minimaux

Culturel

• Utilisation ornementale ou cosmétique lorsqu'un anneau est placé sur un doigt ou lorsqu'un perçage est placé dans l'oreille.
• Dans le nez des bœufs, un cerceau est placé, qui sert à l'attacher et à le contrôler.
• Lorsque l'anneau ou l'anneau est placé dans la main gauche sur l'annulaire, il a une connotation sociale, qui date de l'époque des Grecs anciens, et indique l'engagement, la fidélité et le mariage avec le couple qui porte un cerceau dans le même voie et matériel.

En mécanique

En dehors du contexte ornemental, cosmétique et culturel, le taureau a de nombreuses applications pratiques. En mécanique, le toroïde est utilisé comme anneau de rétention du roulement dans la pointe de l'axe du véhicule. 

Les roulements des véhicules à moteur sont également constitués d'un ou deux cerceaux sous une forme taureau avec diverses formes de section transversale, sur lesquelles ils roulent des cylindres ou des sphères, dans le but de réduire les frottements dans les axes.

En électricité

Dans les applications électriques, le toroïde est également de la plus haute importance, car les noyaux ferromagnétiques des inductances, des électromagers et des transformateurs ont souvent une forme de taureau et sur eux un câble sous la forme d'une bobine.

Le tokamak

Il existe un type de réacteur de fusion contrôlé sous la forme d'un toroïde ou d'un beignet appelé par son nom russe: tOkamak. Dans ce type de réacteur à fusion nucléaire, le récipient et les bobines qui produisent le champ magnétique du confinement du plasma ont une forme ou une disposition toroïdale.

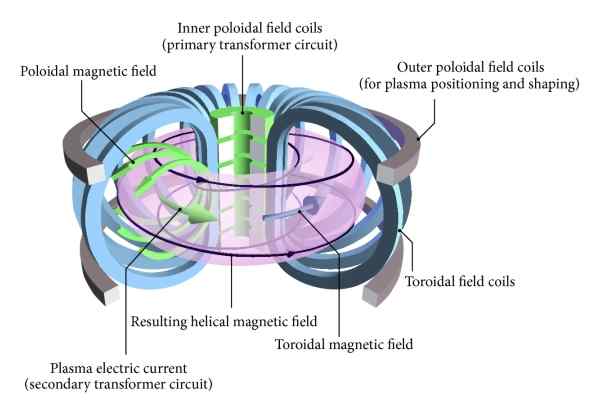La figure montre schématiquement un réacteur à fusion nucléaire contrôlé sous une forme toroïdale connue sous le nom de "tokamak". Dans ce type de réacteur, le plasma, les bobines et le champ magnétique de confinement ont une configuration toroïdale. Source: Wikimedia Commons

Exemples

Surface d'un taureau à section carrée (par formule)

Dans cet exemple, un taureau à section carrée est considéré comme indiqué dans la figure suivante:

Peut vous servir: triangle scaleno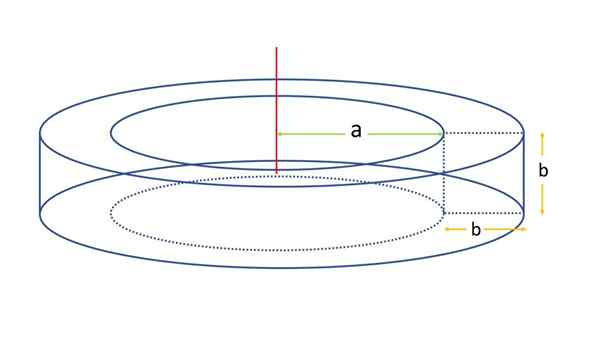 Toroïde de la section carrée. Source: F. Zapata

La surface sera déterminée en utilisant la formule de surface pour un taureau général. À cette fin, il est nécessaire de connaître la distance de l'axe de rotation au centroïde du carré, qui, en utilisant la nomenclature précédente, R:

R = a + b / 2

Il est également nécessaire de connaître le périmètre L de la figure Generatrix qui, comme dans ce cas, est un carré sur le côté b, Son contour sera long:

L = 4⋅b

Ensuite, la formule de surface d'un taureau est appliquée:

S = 2πr⋅l

Le remplacement de R et L pour leurs expressions correspondantes, selon les mesures A et B du taureau carré est:

S = 2π (a + b / 2) ⋅4⋅b = 8π (a + b / 2) ⋅b

Surface toroïde carrée (somme de ses visages)

Le taureau carré de la figure précédente est constitué de quatre faces: la tige et les inférieurs sont des anneaux plats, et l'intérieur et l'extérieur sont cylindriques.

Compte tenu de cela, il est possible de calculer sa surface en ajoutant la superficie de ses quatre faces.

Les faces supérieures et inférieures ont une zone égale à celle du cercle extérieur de rayon (A + B) moins celui du cercle intérieur de la radio pour, qui ont en conséquence:

S_s= S_Toi= π [(a + b)² - b²] = π⋅ [A²+ 2ab]

Le visage cylindrique interne a une zone:

S₁= 2πab

Et la face cylindrique externe a une zone:

S₂= 2π (a + b) b = 2πab + 2πb²

De sorte que la superficie totale du Toroïde sera la somme S_s+S_Toi+S₁+S₂:

A = 2π⋅ [A²+ 2ab] + 2πab + 2πab + 2πb².