Caractéristiques de la prise de vue parabolique oblicuelles, formules, équations, exemples

Il Tir parabolique obcuit Il s'agit d'un cas particulier du mouvement de chute libre dans lequel la vitesse initiale du projectile forme un certain angle avec l'horizontal, résultant en un chemin parabolique.

La chute libre est un cas de mouvement avec une accélération constante, dans laquelle l'accélération est celle de la gravité, qui pointe toujours verticalement vers le bas et a une ampleur de 9,8 m / s ^ 2. Cela ne dépend pas de la pâte du projectile, comme Galileo Galilei l'a démontré en 1604.

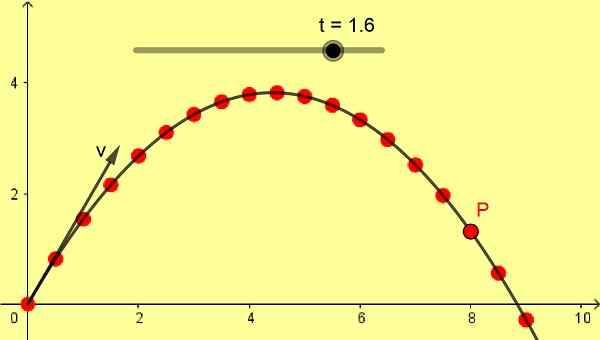Figure 1. Tir parabolique obcuit. (Élaboration propre)

Si la vitesse initiale du projectile est verticale, la chute libre a une trajectoire droite et verticale, mais si la vitesse initiale est oblique, la trajectoire de la chute libre est une courbe parabolique, également démontrée par Galileo.

Des exemples de mouvement parabolique sont la trajectoire qui suit un baseball, la balle tirée par un canon et le jet d'eau qui sort d'un tuyau.

La figure 1 montre un tir parabolique oblique de 10 m / s avec un angle de 60º. L'échelle est en mètres et les positions P successives sont prises avec une différence de 0,1 s à partir du moment initial 0 secondes.

[TOC]

Formules

Le mouvement d'une particule est complètement décrit si sa position est connue, sa vitesse et son accélération en fonction du temps.

Le mouvement parabolique résultant d'un tir oblique est la superposition d'un mouvement horizontal à vitesse constante, plus un mouvement vertical avec une accélération constante égale à l'accélération de la gravité.

Les formules qui s'appliquent au tir parabolique oblique sont celle qui correspond à un mouvement avec une accélération constante a = g, Notez que Bold a été utilisé pour indiquer que l'accélération est un montant vectoriel.

Peut vous servir: satellites naturels

Position et vitesse 

Dans un mouvement d'accélération constant, la position dépend mathématiquement du temps de manière quadratique.

Si nous désignons r(T) La position à l'heure t, rsoit La position instantanée initiale, Vsoit La vitesse initiale, g accélération et t = 0 comme moment initial, la formule qui donne la position pour chaque instant de temps t est:

r(t) = r_soit + V_soit T + ½ g t²

Audacieux dans l'expression précédente indique qu'il s'agit d'une équation vectorielle.

La vitesse en fonction du temps est obtenue en prenant le dérivé par rapport à t de la position et le résultat est:

V(t) = V_soit + g t

Et pour obtenir l'accélération en fonction du temps, la vitesse dérivée de t donnant comme résultat:

pour(t) = g

Lorsque le temps n'est pas disponible, il existe une relation entre la vitesse et la position, qui est donnée par:

V² = Vsoit² - 2 g (et - moi)

Équations

Ensuite, nous trouverons les équations qui s'appliquent à un tir parabolique oblique sous forme cartésienne.

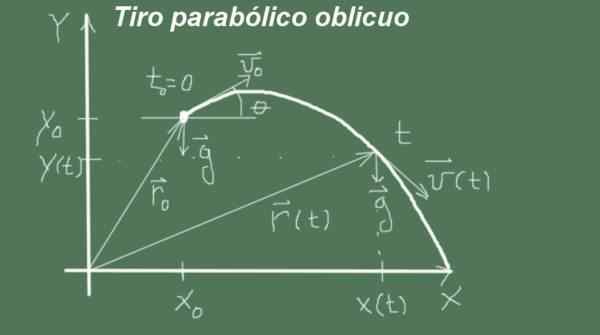
Figure 2. Variables et paramètres du tir parabolique oblique. (Élaboration propre)

Le mouvement commence en ce moment t = 0 Avec position initiale (Xo, moi) et vitesse d'amplitude Vsoit et angle θ, c'est-à-dire que le vecteur de vitesse initial est (Vsoit cosθ, vsoit Senθ). Le mouvement passe avec accélération 

g = (0, -g).

Équations paramétriques

Si la formule vectorielle qui donne la position en fonction du temps est appliquée et que les composants sont regroupés et égalisés, les équations données par les coordonnées de la position à tout moment t seront obtenues.

x (t) = x_soit + V_bœuf t 

et (t) = y_soit + V_Oy t -½ g t²

De même, des équations sont conçues pour les composants de vitesse comme fonction temporelle.

Il peut vous servir: effort normal: ce dont il consiste, comment il est calculé, des exemples

V_X(t) = v_bœuf

V_et(t) = v_Oy - g t 

Où: V_bœuf = Vsoit cosθ; V_Oy = Vsoit Senθ

Équation de trajectoire

y = a x ^ 2 + b x + c

A = -g / (2 Vbœuf^ 2)

B = (vOy/ Vbœuf + g xsoit/ Vbœuf^ 2)

C = (etsoit - VOy Xsoit / Vbœuf)

Exemples 

Exemple 1

Répondre aux questions suivantes:

a) Pourquoi les problèmes de tir parabolique méprisent généralement l'effet de la friction avec l'air?

b) fait la forme de l'objet dans le tir parabolique?

Réponses

a) Pour que le mouvement d'un projectile soit parabolique, il est important que la force de frottement d'air soit bien inférieure au poids de l'objet qui est lancé. 

Si une boule de liège ou un matériau léger est lancé, la force de frottement est comparable au poids et sa trajectoire ne peut pas aborder une parabole.

Au contraire, s'il s'agit d'un objet lourd comme une pierre, la force de frottement est négligeable par rapport au poids de la pierre et sa trajectoire est proche d'une parabole.

b) La forme de l'objet lancé est également pertinente. Si un plata de plan sous la forme d'un avionncito est lancé, son mouvement ne sera pas libre ou parabolique, car la forme favorise la résistance à l'air.

D'un autre côté, si la même feuille de papier est compacte sous la forme d'une balle, le mouvement résultant est très similaire à une parabole.

Exemple 2

Un projectile est lancé à partir du plancher horizontal rapidement de 10 m / s et 60º angle. Ce sont les mêmes données avec lesquelles la figure 1 a été développée. Avec ces données, je trouve:

a) moment où il atteint la hauteur maximale.

Peut vous servir: quelles sont les propriétés thermiques et ce que sont? (Avec des exemples)

b) la hauteur maximale.

c) la vitesse à la hauteur maximale.

d) la position et la vitesse à 1,6 s.

e) Le moment où il joue à nouveau le sol.

f) portée horizontale.

Solution à)

La vitesse verticale en fonction du temps est

V_et(t) = v_Oy - G t = v_soit Senθ - G t = 10 Sen60º - 9.8 t = 8.66 - 9.8 T 

Au moment où la hauteur maximale est atteinte, la vitesse verticale est nulle pour un instant.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Solution b)

La hauteur maximale est donnée par la coordonnée et Pour le moment où cette hauteur est atteinte:

et (0.88S) = Yo je vais t -½ g t ^2 = 0 + 8.66 * 0.88 ½ 9.8 0.88 ^2 = 

3.83 m

Par conséquent, la hauteur maximale est 3.83 m.

Solution C)

La vitesse à la hauteur maximale est horizontale:

V_X(t) = v_bœuf = V_soit cosθ = 10 cos60º = 5 m / s 

D) Solution

La position à 1.6 s est:

X (1.6) = 5 * 1,6 = 8,0 m

et 1.6) = 8.66 * 1.6 ½ 9.8 1.62 = 1.31 m

Solution e)

Lorsque la coordonnée touche et qu'elle est annulée, alors:

et (t) = 8.66 * T -½ 9.8 T2 = 0 ⇒ t = 1,77 s

Solution f)

La portée horizontale est la coordonnée X en ce moment qui joue le sol:

X (1.77) = 5 * 1,77 = 8,85 m

Exemple 3

Trouvez l'équation de trajectoire avec l'exemple 2 données.

Solution 

L'équation paramétrique de la trajectoire est:

x (t) = 5 * t

et (t) = 8.66 * T -½ 9.8 t ^2

Et l'équation cartésienne est obtenue en nettoyant T du premier et en remplaçant dans le second

y = 8.66 * (x / 5) -½ 9.8 (x / 5) ^2

Simplifier:

y = 1,73 x - 0,20 x ^ 2 

Les références

1. P. P. Teodorescu (2007). "Cinématique". Systèmes mécaniques, modèles classiques: mécanique des particules. Springer.
2. Resnick, Halliday & Krane (2002). Volume physique 1. CECSA, Mexique.
3. Thomas Wallace Wright (1896). Éléments de la mécanique, y compris la cinématique, la cinétique et les statistiques. E et FN Spon.
4. Wikipédia. Mouvement parabolique. Récupéré de es.Wikipédia.org.
5. Wikipédia. Mouvement d'un projectile.Récupéré de.Wikipédia.org.