Types d'angles, caractéristiques et exemples

Il y a divers Types d'angles, En tenant compte de plusieurs critères pour les différencier, par exemple, ils peuvent être distingués par leur mesure, par la position qu'ils occupent et également selon la somme avec d'autres angles.

Habituellement, un angle est défini comme l'ouverture entre deux semi-sortants avec une origine commune, appelée le sommet de l'angle. La amplitude L'ouverture est la mesure de l'angle, qui vient fréquemment en degrés ou en radians.

Un degré équivaut à l'une des 360 parties dans lesquelles une circonférence peut être divisée. Si la circonférence est divisée en deux parties égales, chacune est égale à 180 degrés ou 180 °, si plutôt elle est divisée en quatre parties égales, chacune sera de 90 ° et ainsi de suite. Ce système est appelé Sexagesimal.

Radianes est une autre mesure très utilisée, qui consiste à prendre une circonférence et à mesurer l'angle entre deux de ses radios, dont la longueur est "R" et avec le sommet au centre de la circonférence. De cette façon, l'arc "S" entre ces radios est également affirmé "R" et l'angle sous-tendance est alors 1 radián ou 1 rad et égal à 57.3e degrés.

L'instrument pour mesurer les angles est le convoyeur. Pour prendre une mesure, le centre du transporteur est coïncidé avec le sommet de l'angle et l'un des côtés de la même chose avec la ligne de 0º du transporteur. L'autre côté coïncide avec la mesure de l'angle, qui est lue sur l'échelle.

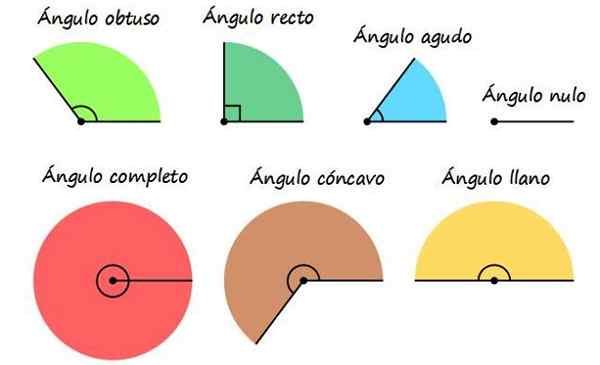
Types d'angles selon votre mesure

Classification des angles par leur mesure. Source: Wikimedia Commons.

L'une des façons les plus fréquentes de se référer aux angles est de les nommer en fonction de leur mesure, bien qu'un angle puisse appartenir à plus d'une catégorie de décrit ci-dessous.

Peut vous servir: coefficient de variation: à quoi sert-il, calcul, exemples, exercices

Angle nul

Celui dont la mesure est de 0º ou 0 rad, c'est-à-dire que les deux semi-sorts ont une ouverture zéro.

Angle aigu

La mesure d'un angle aigu est comprise entre 0 et 90 ° ou entre 0 et π / 2 Radians. Par exemple, les angles de 30 °, 45º et 60º, qui font partie des angles notables, sont tous des angles aigus.

Angle droit

C'est celui qui mesure exactement 90 ° (π / 2 radians), cela signifie que les semi-structures qui la définissent sont perpendiculaires.  Les angles internes d'un carré ou d'un rectangle sont des angles droits, et c'est aussi un angle droit qui se forme entre les cathétes d'un triangle rectangle.

Angle obtus

C'est un angle supérieur à 90 ° ou π / 2 radians.

Angle plat

Il mesure exactement 180 °, équivalent à π radians. Lorsqu'une ampleur vectorielle est opposée à une autre, elle forme un angle de 180 °, par exemple la vitesse d'un mobile qui se déplace en ligne droite et la décélération ressentie lors de son arrêt.

Angle convexe

Chaque fois qu'un angle mesure moins de 180 ° est un angle convexe. Un angle aigu peut être convexe, comme l'un des 90 ° et ces angles obtus dont la mesure est incluse dans 90 ° et 180º. Plus d'exemples d'angles convexes sont:

• 45º
• 60º
• 75º
• 135º

Angle concave

C'est celui qui mesure plus de 180 °, comme 225 ° ou 270 °, ce dernier est égal à trois quarts de la circonférence.

Angle complet ou périgonal

Sa mesure est à 360 ° ou 2π radiares. Cela signifie que les deux semi-structures qui ralentissent coïncident à nouveau, mais contrairement à l'angle nul, dans ce cas, il y a eu un tour complet.

Peut vous servir: ovale (figure géométrique): caractéristiques, exemples, exercices

Types d'angles en fonction de la position de leurs côtés

Dans de nombreuses figures et structures géométriques, plus d'un angle apparaît et c'est pourquoi il est pratique d'avoir un critère pour comparer les côtés de l'un par rapport à un autre. De cette façon, ils ont:

Angles consécutifs

Les angles consécutifs sont côte à côte, ils ont donc un côté commun et un sommet.

Angles adjacents

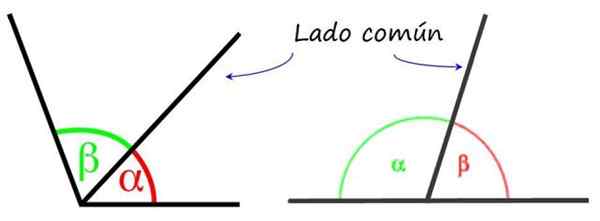À gauche deux angles consécutifs et à droite deux angles adjacents. Source: Wikimedia Commons / F. Zapata.

Les angles adjacents ont un côté commun et un sommet, c'est-à-dire qu'ils se présentent à côté de l'autre. Mais contrairement aux angles consécutifs, aux angles adjacents, les côtés restants sont en opposés semi-sortants, donc entre les deux angles au total 180º.

Angles opposés par le sommet

Les angles opposés par le sommet ont le sommet en commun, et leurs côtés s'étendent en face, de l'un des angles à l'autre. De cette façon, les angles opposés par le sommet ont la même mesure.

La figure suivante montre 4 angles, indiqués avec des lettres grecques. Les angles bleus sont α et β, et comme on peut le voir, ce sont des angles aigus et opposés par le sommet. D'un autre côté, les angles γ et Δ sont des angles obtus et sont également opposés par le sommet.

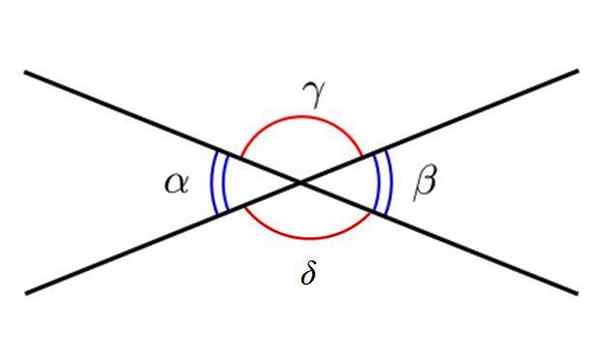Angles opposés par le sommet. Source: Wikimedia Commons.

Types d'angles selon la somme de leurs mesures

Certains calculs, en particulier en trigonométrie, sont très simplifiés en observant si la somme des mesures de deux angles est celle de l'un des angles notables, comme l'angle droit (90º) ou l'angle plat (180º). Selon cela, ils ont:

Angles complémentaires

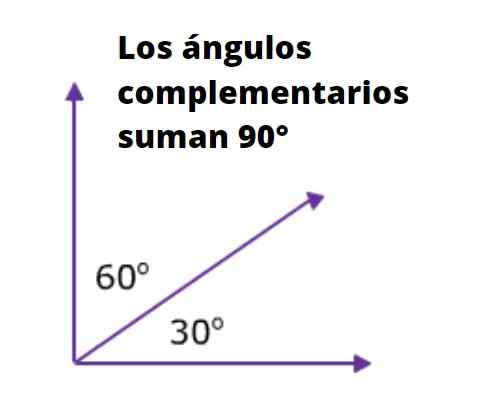
Ces angles dont la somme est égal à 90º sont complémentaires. Par exemple, les angles aigus internes d'un triangle rectangulaire sont complémentaires, car la somme de ses trois angles internes est égal à 180º.

Peut vous servir: 90 diviseurs: quelles sont et explications

Étant donné que l'un des angles internes du triangle rectangle mesure 90 °, la somme des deux autres est également égale à 90º.

Angles supplémentaires

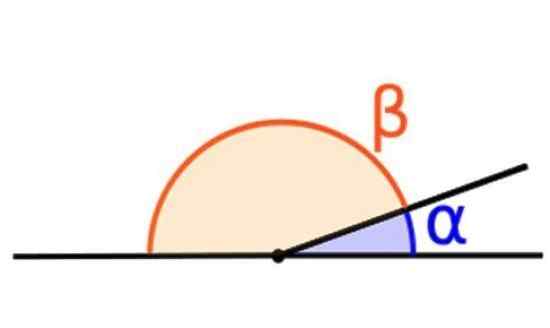La somme de deux angles supplémentaires est égal à 180º. Source: Wikimedia Commons.

Sont ces angles dont la somme est égale à 180º. Par exemple, les angles α et β montrés dans la figure supérieure.

Des exemples d'angles notables qui sont en même temps supplémentaires sont:

• 120º et 60º
• 135º et 45º

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Baldor. 1983. Géométrie plate et espace et trigonométrie. Groupe de patrie culturelle.
3. ET. POUR. 2003. Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
4. Géométrie 1ère. Angles dans la circonférence. Récupéré de: edu.Xunta.est.
5. Riche, b. Géométrie. 1991. Série Schaum. 2e. Édition. McGraw Hill.