Types de fonctions et leurs graphiques

- 2388
- 353
- Adam Mercier
Il y a divers Types de fonctions qui sont utilisés pour modéliser les problèmes des branches de connaissances telles que les sciences naturelles, l'administration, l'économie et les sciences sociales. Mathématiquement parlant, une fonction est une relation entre deux ou plusieurs variables.
Plusieurs fois, certains objets ou quantités sont liés les uns aux autres. Ces montants sont représentés par des variables. Par exemple, il existe deux variables apparentées, appartenant à deux ensembles A et B, pas nécessairement numériques, bien que la plupart du temps ils soient-.
Pour être considéré comme une fonction, cette relation doit remplir deux conditions: la première est que tous les éléments de l'ensemble de départ pour participer, et le second, que chaque élément de cet ensemble est lié à un seul des éléments de l'ensemble B.
Les variables sont généralement appelées avec des lettres X et et, avec X comme la variable indépendante et et comme la variable dépendante. Naturellement, ils peuvent être appelés d'une autre manière, en choisissant le nom de la variable conformément à l'ampleur qu'il représente.
La relation entre les deux est indiquée par la lettre F -ou une autre lettre de l'alphabet, et est représentée de plusieurs manières, comme un ensemble de paires ordonnées, un graphique, une expression verbale ou une formule algébrique:
- f (x) = x + 1
- Population p d'une certaine ville dans un certain intervalle de temps t.
- H (x) = (1,3); (2,4); (3,5); (4.6)
Les fonctions sont caractérisées par domaine et gamme ou route. Le domaine est l'ensemble des valeurs que la variable X Vous pouvez prendre, tandis que la plage est l'ensemble de valeurs qui acquiert la fonction dépendante ou la variable et.
Classification des fonctions
Les fonctions peuvent être regroupées en 5 grandes catégories, comme en témoigne le schéma suivant, dans lequel chaque groupe est étiqueté avec un numéro romain et une couleur. En partant de gauche à droite, les fonctions sont classées selon:
- I) sa forme.
- Ii) Symétrie.
- Iii) le moyen d'exprimer la variable.
- Iv) sa continuité et sa monotonie.
- V) La façon dont les éléments du domaine sont liés à ceux de la gamme.
 Principaux critères de classification des fonctions. Source: F. Zapata.
Principaux critères de classification des fonctions. Source: F. Zapata. Suivez maintenant une brève description de chacun des types de fonctions avec leurs exemples respectifs.
I) Fonctions en fonction de sa forme
Toi.1) fonctions algébriques
Ils sont parmi les fonctions les plus utilisées dans de nombreux domaines de la science, et ils sont donc les plus connus. Ils sont caractérisés par une règle de correspondance, une expression algébrique.
À leur tour, les fonctions algébriques sont subdivisées dans les types suivants:
- Toi.1.a) polynôme ou polynôme.
- Toi.1.b) rationnel.
- Toi.1.c) irrationnel.
- Toi.1.d) par sections.
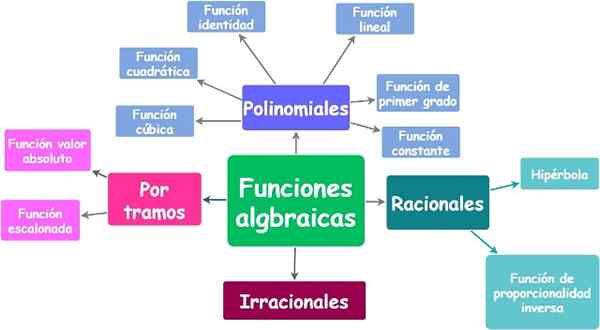 Fonctions algébriques et leurs types. Source: F. Zapata.
Fonctions algébriques et leurs types. Source: F. Zapata. Toi.1.a) fonctions polynomiales ou polynomiales
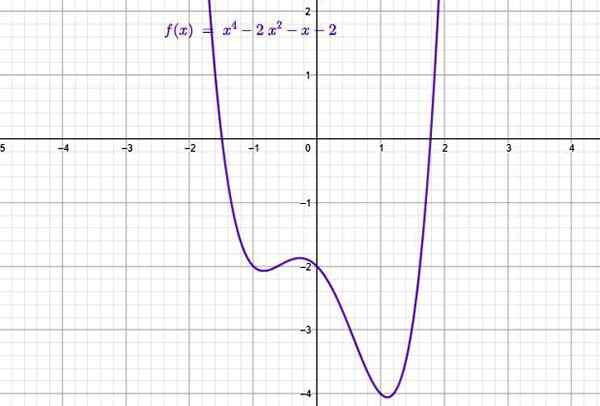 Exemple de fonction de type polynôme. Source: F. Zapata à travers Geogebra.
Exemple de fonction de type polynôme. Source: F. Zapata à travers Geogebra. Ils sont constitués de sommes de termes dont la forme générale est:
P (x) = anXn + pour N-1XN-1 +… pour1x + a0
Où les coefficientsn, pour N-1… pour1, pour0 Ce sont des nombres réels et n est un entier. Le domaine des fonctions polynomiales est l'ensemble des nombres réels et sont également des fonctions continues dans tout ce domaine.
Dans la figure supérieure se trouve le graphique de la fonction polynomiale suivante de l'ordre 4:
f (x) = x4 - 2x2 - x -2
Parmi les fonctions polynomiales, certains cas particuliers se distinguent, selon les valeurs des coefficients. Il convient de considérer attentivement, car ils sont très utiles dans plusieurs situations:
i) Fonction constante
Il existe une fonction constante lorsque tous les coefficients sont annulés, sauf0:
f (x) = a0 = k
Le graphique de la fonction constante est une ligne droite parallèle à l'axe horizontal, comme les lignes:
- f (x) = 2
- g (x) = π
- H (x) = -3/2
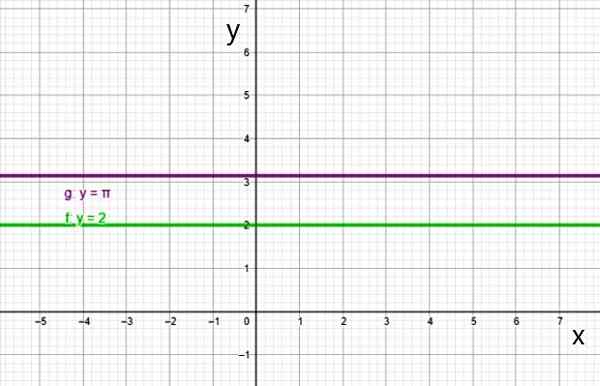 Deux exemples de fonction constante. Source: F. Zapata.
Deux exemples de fonction constante. Source: F. Zapata. Ii) Fonction au premier degré
La première fonction ou la fonction connexe est celle dont le graphique est une ligne droite. C'est un cas particulier de la fonction polynomiale où tous les coefficients de l'anneau1 déjà0. Il est donné par:
f (x) = a1x + a0
La valeur A1 C'est la pente de la ligne, qui donne une mesure de son inclination, et0 C'est la coupe de la ligne avec l'axe vertical. Les deux peuvent prendre des valeurs positives ou négatives.
Des exemples de fonction au premier degré sont les suivants:
- G (x) = 2x -1
- H (x) = -6x +5/2
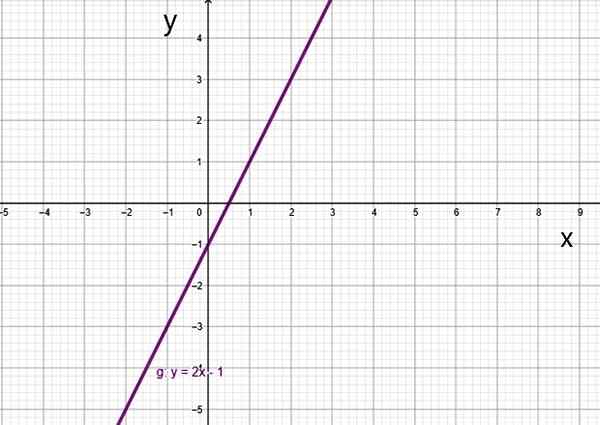 Fonction du premier degré f (x) = 2x-1. Source: F. Zapata.
Fonction du premier degré f (x) = 2x-1. Source: F. Zapata. Il y a un cas spécial, qui est la fonction linéaire.
Peut vous servir: mesures de tendance centrale pour les données groupées: formules, exercicesiii) Fonction linéaire
Lorsque le coefficient de0 C'est 0, la fonction passe toujours par l'origine et est exprimée par f (x) = a1X, appelant Funtion linéaire, comment ça va:
- f (x) = 5x
- G (x) = -7x
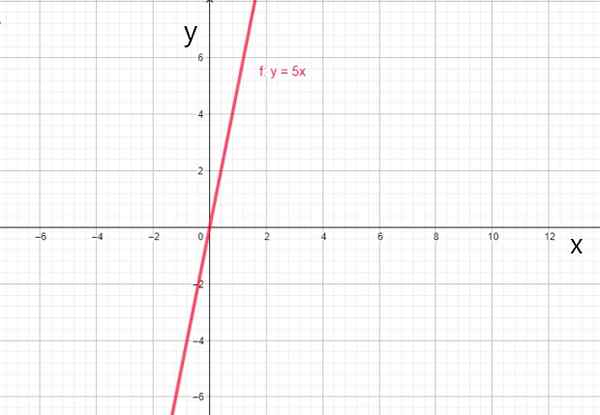 Fonction linéaire f (x) = 5x. Source: F. Zapata.
Fonction linéaire f (x) = 5x. Source: F. Zapata. iv) Fonction d'identité
C'est un cas particulier de la fonction linéaire, dans laquelle1 = 1:
f (x) = x
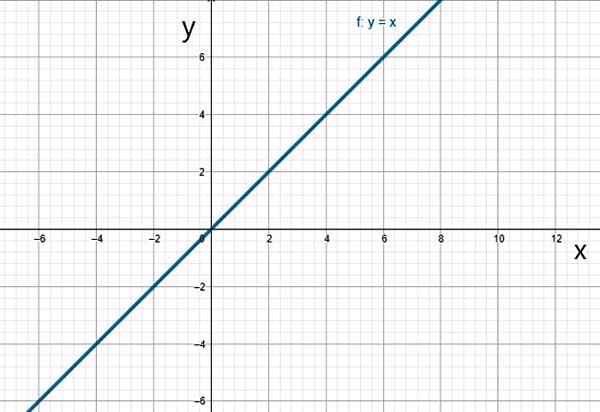 La fonction d'identité. Source: F. Zapata.
La fonction d'identité. Source: F. Zapata. v) Fonction quadratique
Il a la forme générale:
f (x) = a2X2 +pour1x + a0
Avec un2 ≠ 0.
Son graphique est une parabole dont l'axe axial ou symétrie est parallèle à l'axe des ordonnées. Coupe toujours l'axe vertical au point de coordonnées x = 0, y = a0. Quant aux intersections avec l'axe horizontal, il peut avoir jusqu'à un maximum de 2.
Des exemples de fonctions quadratiques sont:
- f (x) = x2 - 3x - 4
- G (x) = 4x2
- H (x) = x2-1
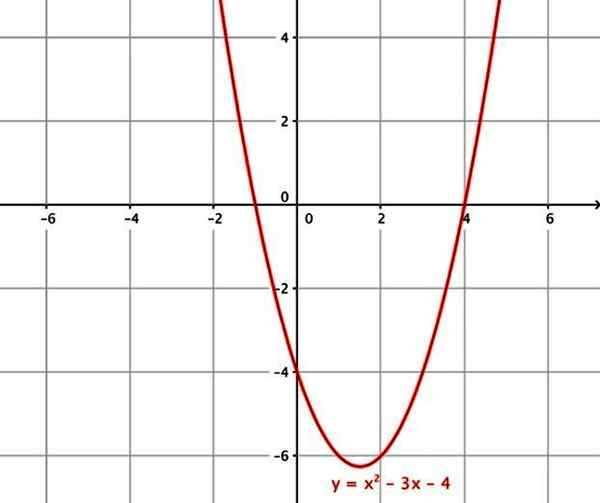 La fonction quadratique. Source: Wikimedia Commons.
La fonction quadratique. Source: Wikimedia Commons. vi) fonction cubique
Comme son nom l'indique, la fonction cubique contient une puissance de 3:
f (x) = a3X3 + pour2X2 + pour1x + a0
Le coefficient un3 Il est toujours différent de 0, comme dans ces cas:
- f (x) = x3
- G (x) = 5x3 - 2
- H (x) = -3x3 + 4x2 + 10x + 1
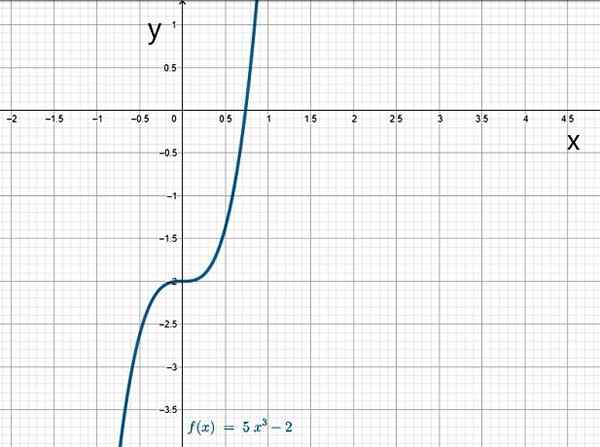 Fonction cubique. Source: F. Zapata.
Fonction cubique. Source: F. Zapata. Toi.1.b) fonctions rationnelles
Les fonctions rationnelles ont la forme:
=\fracP(x)Q(x))
À partir du domaine des fonctions rationnelles, toutes les valeurs qui annulent le dénominateur Q (x), c'est-à-dire ses racines, tandis que les valeurs des valeurs des valeurs des et qui déterminent les asymptotes horizontaux.
Une asymptote est une ligne à laquelle la fonction approche, à gauche et à droite, au-dessus ou en dessous, mais ne traverse jamais. Ces lignes peuvent être verticales, horizontales ou inclinées.
Des exemples de fonctions rationnelles sont:
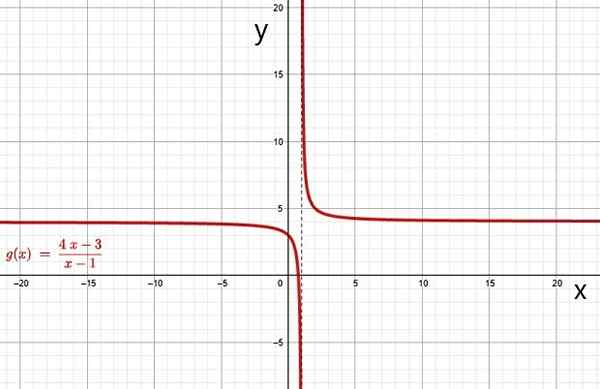 Fonction rationnelle. Source: F. Zapata à travers Geogebra.
Fonction rationnelle. Source: F. Zapata à travers Geogebra. i) Hyperbole
Le graphique d'une fonction rationnelle est une hyperbole lorsque le polynôme dans le dénominateur q (x) a un grade 1. Le graphique des fonctions f (x) et g (x) des exemples ci-dessus sont des hyperbolas, il peut être facilement vérifié via un logiciel graphique en ligne gratuit, comme Geogebra.
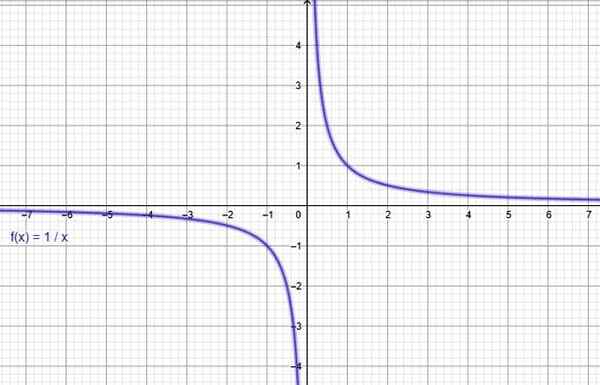 La fonction y = 1 / x. Source: F. Zapata à travers Geogebra.
La fonction y = 1 / x. Source: F. Zapata à travers Geogebra. Ii) Fonction de proportionnalité inverse
C'est une fonction de forme:
Où c est un nombre réel différent de 0. Son domaine est l'ensemble des nombres réels sauf 0.
Toi.1.c) fonctions irrationnelles
Sont ceux dont la variable indépendante est sous un signe radical. Sa forme générale est:
Certaines de ces fonctions peuvent être:
Le domaine de ces fonctions est déterminé comme suit:
-Si les racines sont d'un indice de couple, la quantité subradique f (x) doit toujours être 0 ou positive.
-Lorsque les racines sont étranges, F (x) peut être positif ou négatif. Par conséquent, dans ce cas, le domaine de la fonction est les nombres réels.
Par exemple, le domaine de:
C'est l'ensemble des nombres réels tels que X-3 est supérieur ou égal à 0. Dans ce cas, x doit être supérieur ou égal à 3. Par conséquent, le domaine de cette fonction est l'ensemble des valeurs de l'intervalle [3, ∞ +).
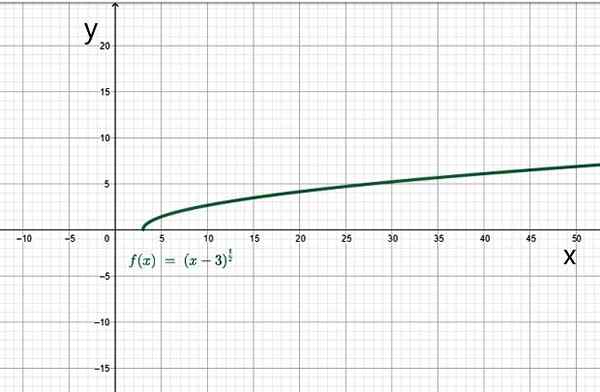 Exemple de fonction irrationnelle. Source: F. Zapata.
Exemple de fonction irrationnelle. Source: F. Zapata. Toi.1.d) Fonctions en pièces ou par sections
La fonction en parties, par sections ou pièces est celle qui nécessite plus d'une formule pour différentes valeurs de domaine. Voici quelques exemples de votre application:
-Tarifs pour l'envoi de colis par courrier, selon le poids ou le volume, l'origine et la destination de la même.
-Tarifs pour les services, par exemple la téléphonie et l'électricité.
-Vente de billets pour les musées ou les parcs d'attractions, selon l'âge.
Sous forme mathématique, une fonction en parties peut être, par exemple:
Le domaine d'une fonction en parties dépend de sa définition. Dans l'exemple précédent, le domaine est l'ensemble formé par: (-∞, -1) ∪ [1, + ∞).
Ii) Fonction Escalonada
Le graphique de cette fonction par sections se compose d'étapes, telles que celles d'une échelle ou peut être de hauteurs différentes, selon la façon dont la fonction est définie.
Il peut vous servir: Hipparco de Nicea: biographie et contributions à la sciencePour cela, un intervalle fini [a, b] est choisi qui contient un certain nombre fini de discontinuités, appelées xToi < x1 < x2 <… . xn Et un intervalle ouvert est choisi (xToi , Xi + 1) Pour lui donner une constante de valeur sToi, Avec les sauts aux points xToi. La valeur de sToi C'est la hauteur de l'étape en question.
Un exemple de fonction échelonnée est la partie entière, qui prend un nombre et l'associe à l'entier suivant, soit par excédent, soit par défaut. Ce qui suit est une partie entière:
[x] = (plus grand entier ≤ x)
Selon cette fonction, toute la partie de 2.5 est:
[2.5] = (plus grand entier ≤ 2.5) = 2
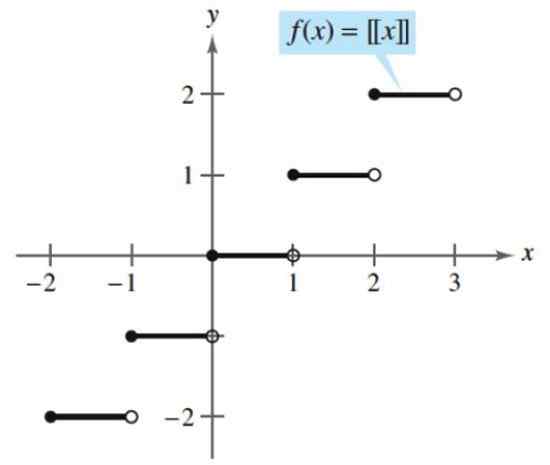 Toute la partie de. Source: Larson, R. Calcul avec géométrie analytique. McGraw-Hill.
Toute la partie de. Source: Larson, R. Calcul avec géométrie analytique. McGraw-Hill. Toi.2) fonctions transcendantes
Les fonctions non algébriques sont appelées transcendantes. Les fonctions exponentielles, logarithmiques et trigonométriques sont des fonctions transcendantes.
En eux la variable X Il fait partie de l'argument de la fonction ou dans le cadre de l'exposant ou de l'indice d'une racine, par exemple:
- f (x) = log (x + 1)
- H (x) = -0.2⋅8-3x
Les fonctions transcendantes ont de nombreuses applications, par exemple dans l'étude des vibrations et des ondes, des distributions de probabilité, de la modélisation des vagues, de la croissance de diverses populations, de la désintégration radioactive, des taux d'intérêt et bien d'autres.
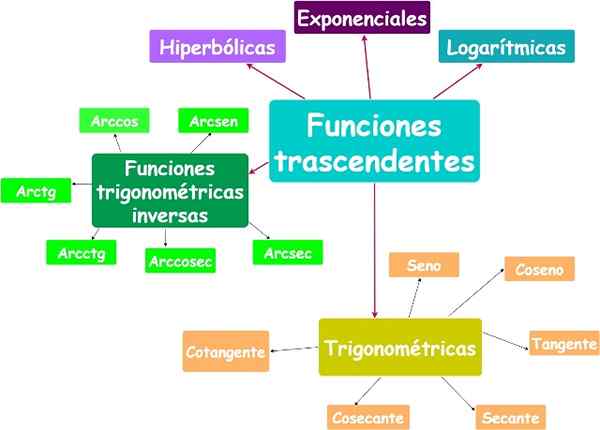 Fonctions transcendantes principales. Source: F. Zapata.
Fonctions transcendantes principales. Source: F. Zapata. Toi.2.a) Fonction exponentielle
La fonction exponentielle est définie par:
f (x) = aX
Où a est la base, qui est toujours un nombre positif de 1, et la variable, un nombre réel, apparaît dans l'exposant. En général, la fonction exponentielle est écrite:
f (x) = a⋅aBx
Ici A et B sont de vrais coefficients. Voici les fonctions de ce type:
- f (x) = 5eX
- H (x) = 4. dix5x
- g (t) = 8e-2t
Base et, où et C'est le nombre d'Euler 2.71828 ..., apparaît fréquemment dans les problèmes de science et d'ingénierie, ainsi que des statistiques. Lorsque la fonction a cette base Fonction exponentielle naturelle.
Le domaine de la fonction exponentielle est l'ensemble des nombres réels, tandis que la plage est les nombres positifs.
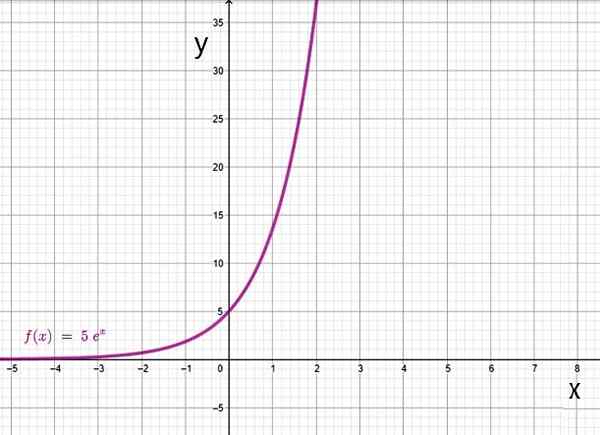 Fonction exponentielle basée sur. Source: F. Zapata à travers Geogebra.
Fonction exponentielle basée sur. Source: F. Zapata à travers Geogebra. Toi.2.b) Fonction de logarithme
Pour sa part, la fonction de logarithme basée sur pour C'est la fonction inverse de la fonction exponentielle basée sur pour. Ouais:
enregistrerpour x = y
Ensuite:
x = aet
En particulier, si la base du logarithme est le numéro E, la fonction est appelée Fonction de logarithme népérienne Et il est désigné comme LN. Les fonctions de ce type sont:
- f (x) = ln x
- g (x) = log (x + 1)
- H (t) = 1 - log x2
Le domaine de la fonction de logarithme, quelle que soit la base, sont les nombres réels positifs, sans compter le 0. C'est-à-dire qu'il n'y a pas de logarithmes de nombres négatifs ou 0.
Cependant, un logarithme peut être 0 ou négatif: le logarithme du nombre entre 0 et 1 est négatif et pour sa partpour 1 = 0.
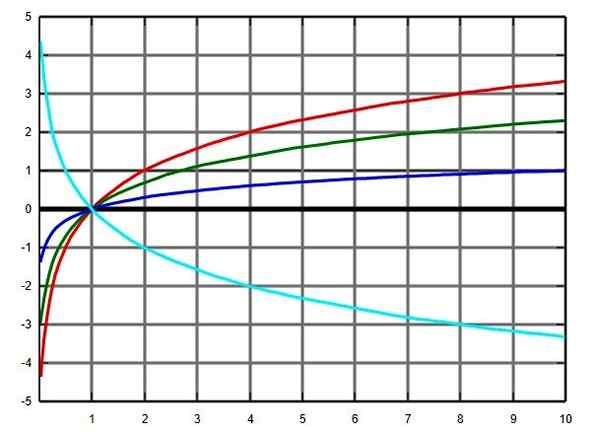 Graphique de fonction de logarithme dans plusieurs bases: base 2 en rouge, vert e, base bleu et turquoise sur la base 0.5. Source: Wikimedia Commons.
Graphique de fonction de logarithme dans plusieurs bases: base 2 en rouge, vert e, base bleu et turquoise sur la base 0.5. Source: Wikimedia Commons. Toi.2.c) fonctions trigonométriques
Ce sont ceux qui viennent des raisons trigonométriques: sinus, cosinus, tangent, séchage, harmoning et cotangent d'un angle x. Ils sont désignés respectivement comme:
Sen X, Cos X, Tg X, Sec X, Harm x et Cotg X
Ce sont des fonctions périodiques, ce qui signifie que sa forme est répétitive, ils sont donc très utiles pour décrire des phénomènes naturels tels que les signaux, les oscillations, les mouvements circulaires et les mouvements de swing, qui se caractérisent par le fait d'être répétitif.
Des exemples de fonctions trigonométriques sont:
- f (x) = sin x
- G (t) = 5⋅cos (ωt + π)
- H (x) = tg (x / 2)
Variable x est exprimé en radianes.
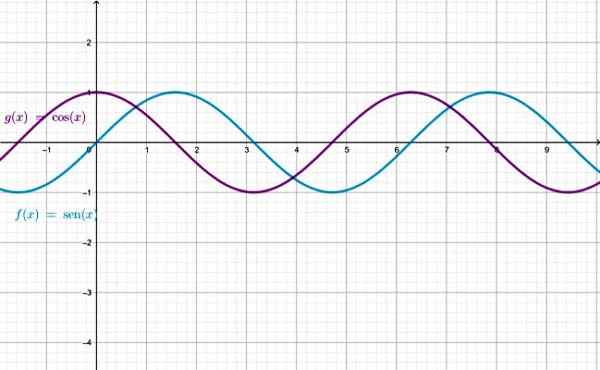 Graphique des fonctions sen x et cos x, notez qu'ils sont identiques, sauf que l'un est déplacé par rapport à l'autre. Source: F. Zapata à travers Geogebra.
Graphique des fonctions sen x et cos x, notez qu'ils sont identiques, sauf que l'un est déplacé par rapport à l'autre. Source: F. Zapata à travers Geogebra. La maîtrise des fonctions Sen X et Cos X, est l'ensemble des nombres réels. Pour les fonctions restantes, il existe des valeurs x pour lesquelles la fonction n'est pas définie:
-La fonction Tg x n'existe pas lorsque x = ± π / 2, ± 5π / 2 ... c'est, tous les multiples impairs de π / 2.
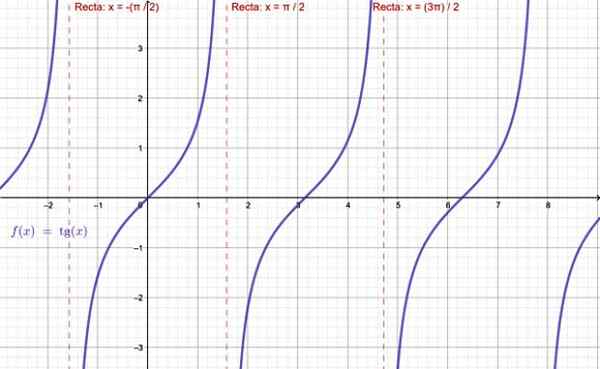 Graphique de la fonction tangente. Source: F. Zapata à travers Geogebra.
Graphique de la fonction tangente. Source: F. Zapata à travers Geogebra. -Quant à f (x) = cotg x, cette fonction n'est pas définie pour les multiples entiers de π: ± π, ± 2π, ± 3π ..
Peut vous servir: loi des signes-La fonction y = sec x n'est pas valide lorsque cos x = 0, qui exclut x = ± π / 2, ± 5π / 2… de son domaine.
-Enfin, pour f (x) = dommage x, les multiples entiers de π n'appartiennent pas à leur domaine.
Toi.2.d) fonctions hyperboliques
Les fonctions hyperboliques sont des combinaisons spéciales d'exponentives etX et e-X Et ils sont appelés comme le sein, coseno .. .hyperbolique. Comme pour les fonctions trigonométriques, également appelées "circulaire", il existe 6 fonctions hyperboliques:
-Sinus hyperbolique Senh X:
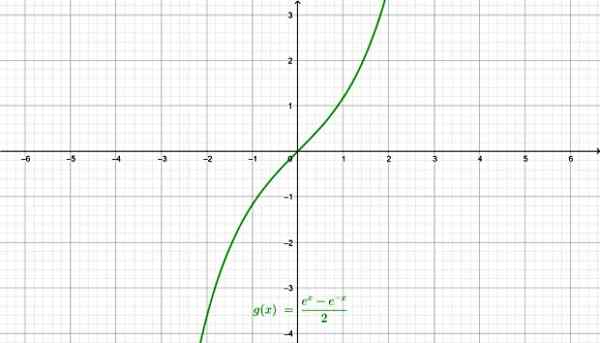 La fonction du sinus hyperbolique. Source: F. Zapata à travers Geogebra.
La fonction du sinus hyperbolique. Source: F. Zapata à travers Geogebra. -Cosinus hyperbolique COSH X:



-Cotangente hyperbolique Coth x:
Un câble flexible, fait de matériau uniforme et suspendu entre deux points, prend la forme d'une courbe appelée caténaire, qui est exprimé comme un cosinus hyperbolique:
Toi.2.e) fonctions trigonométriques inverses
Ils correspondent à l'inverse des fonctions trigonométriques. Par exemple, quel serait l'angle (arc) dont la sein vaut 0.5?
La réponse est arc sen 0.5, qui se lit comme suit «Arc Sinus de 0.5 ”, et cet angle est de 30 °, bien qu'en principe, ce ne serait pas le seul angle dont le sein vaut 0.5, puisque la fonction Sen X est périodique. Ce qui se passe, c'est que si la fonction Sen x est prise dans tout son domaine, elle n'aurait pas inverse, donc la fonction Arcoseno n'a pas pu être définie. Le problème est réglé en restreignant tout aux angles entre -π / 2 et + π / 2.
Cela peut être exprimé comme suit:
Si arc sen x = θ, cela signifie que sin θ = x
Avec -π / 2 ≤ θ ≤ π / 2.
Une autre notation utilisée pour l'arc sen x est f (x) = péché-1 X. Le graphique est illustré ci-dessous:
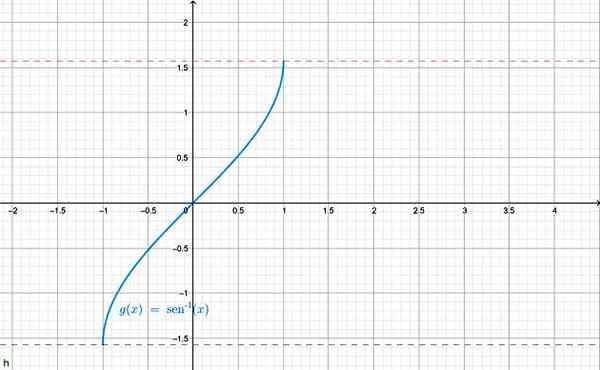 Arcsen x Function Graphics. Source: F. Zapata à travers Geogebra.
Arcsen x Function Graphics. Source: F. Zapata à travers Geogebra. Il est également possible de définir l'inverse pour les autres fonctions trigonométriques, par exemple: arc cos x = θ et donc. Pour chacun, le rang est correctement restreint, être l'inverse de la fonction trigonométrique correspondante.
Ii) Fonctions en fonction de sa symétrie
Ii.1) pair
Si pour tous les x appartenant au domaine de f (x), il est accompli que:
f (x) = f (-x)
On dit que la fonction est même, comme celles qui suivent:
- f (x) = x2 - 3
- g (x) = cos x
 Exemple d'une fonction de paire. Source: F. Zapata à travers Geogebra.
Exemple d'une fonction de paire. Source: F. Zapata à travers Geogebra.
Par exemple, faire x = 1 en f (x) = x2 - 3 Est obtenu:
f (1) = 12 - 3 = -2.
Et si x = -1, alors:
f (-1) = (-1)2 - 3 = -2.
Les deux résultats sont identiques.
Les fonctions uniques ont une symétrie autour de l'axe vertical, comme on peut le voir dans la figure précédente.
Ii.2) Fonction étrange
D'un autre côté, oui:
f (-x) = -f (x)
La fonction est étrange.
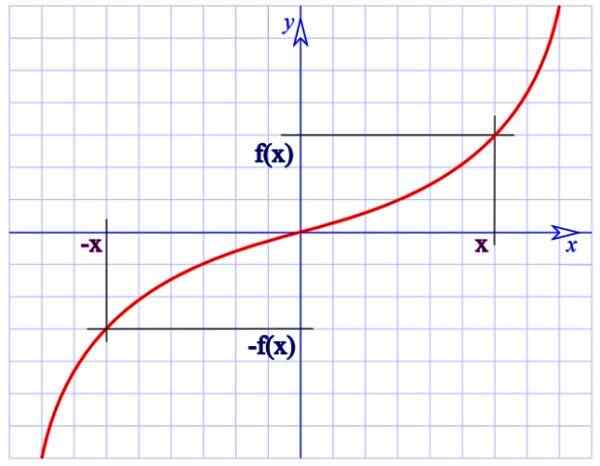 Une fonction étrange. Source: Wikimedia Commons.
Une fonction étrange. Source: Wikimedia Commons. Par exemple, la fonction f (x) = 1 / x de la figure supérieure est impair, puisque:
f (-x) = -1 / x
ET
-f (x) = -1 / x
Une autre fonction impar importante est f (x) = sin x.
Notez que les fonctions impaises ont une symétrie de rotation de 180 ° autour de l'origine (le graphique n'est pas modifié si chaque point est tourné à 180 ° en ce qui concerne l'origine des coordonnées).
Iii) fonction en fonction de l'expression de la variable
III.1) Fonctions explicites
Ils sont exprimés directement en termes de variable dépendante comme y = f (x). Par exemple:
- f (x) = x3
III.2) Fonctions implicites
Dans les fonctions implicites, aucune des variables ne semble claire. Ils sont exprimés comme f (x, y) = 0, comme:
- X2 + et2 -3xy = 0
- xy = - x2+ X-5
Les fonctions décrites tout au long de cet article sont des fonctions explicites.
Iv) Fonctions en fonction de vos graphiques
Selon leur graphique, les fonctions peuvent être continues ou discontinues. Les fonctions continues peuvent être tracées sans interrompre la course, en revanche, les fonctions discontinues présentent des sauts. Dans l'image suivante, la fonction est discontinue à x = a:
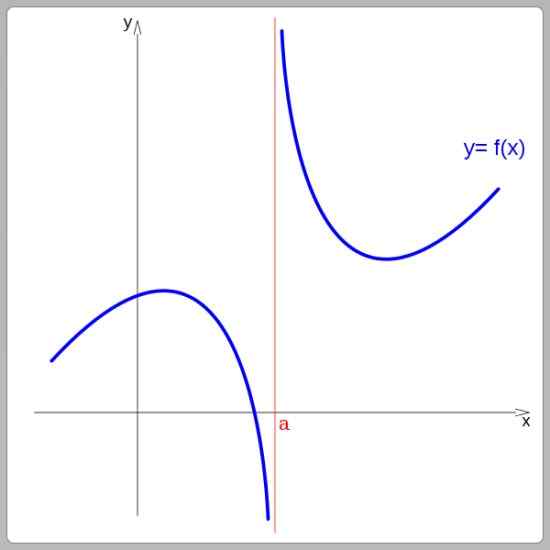 Fonction de discontinuité à x = a. Source: Wikimedia Commons.
Fonction de discontinuité à x = a. Source: Wikimedia Commons. Des exemples de fonctions continues sont la fonction linéaire, la fonction quadratique et les fonctions sinus et cosinus. Et parmi les fonctions discontinues figurent la fonction échelonnée et la fonction tangente.
V) Fonctions en fonction de la relation entre les éléments du domaine et la gamme
V.1) Fonction d'injective
Une fonction est Injectif Lorsqu'il n'y a pas deux éléments différents dans l'ensemble de départ ou de domaine, qui ont la même image dans l'ensemble d'arrivée.
Supposons que les fonctions réelles l'ont été, sauf indication contraire, par exemple:
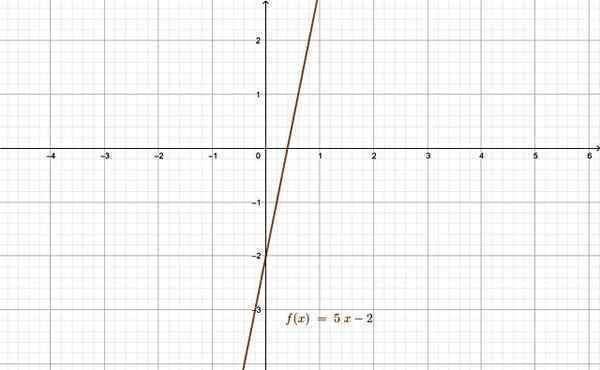
f (x) = 5x -2
Toute la valeur X appartenant au domaine de f (x), qui est l'ensemble ℛ des nombres réels, a une image unique, également réelle. D'un autre côté, dans cette autre fonction:
g (x) = x2
Il existe différents éléments dans le domaine qui ont la même image, par exemple x1= 2 et x2= -2:
G (2) = g (-2) = 4.
La façon d'identifier une fonction injective de son graphique est de dessiner une ligne horizontale, si elle est coupée à la courbe à plus d'un point, la fonction n'est pas injectée.
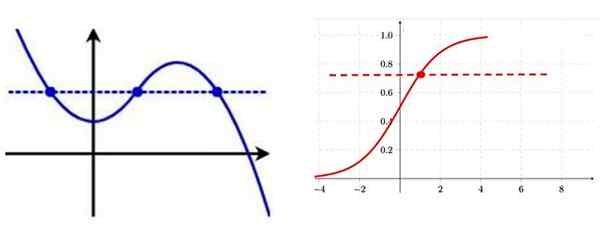 À gauche une fonction injective non, notez qu'il y a plusieurs points du graphique avec la même coordonnée verticale. Sur la droite, une fonction injective, à chacun des points de la courbe, il a une coordonnée «y» particulière. Source: F. Zapata.
À gauche une fonction injective non, notez qu'il y a plusieurs points du graphique avec la même coordonnée verticale. Sur la droite, une fonction injective, à chacun des points de la courbe, il a une coordonnée «y» particulière. Source: F. Zapata. V.2) Fonction de surcouchage
Dans fonctions onjectives, Tous les éléments de l'ensemble d'arrivée sont l'image d'un élément de l'ensemble de départ. Un exemple de fonction de sur-place est le même f (x) = 5x -2, mais g (x) = x2 Ce n'est pas le cas, car les valeurs prises g (x) ne sont que les vraies positives et les 0.
Cependant, le domaine pourrait être redéfini de sorte que G (x) était sur place, si par exemple, il passe à tous les vrais positifs plus 0.
V.3) fonction bijective
Enfin, une fonction qui est à la fois injective et sur-objectif, est appelée Bijectif. Des exemples de fonctions bijectives sont: la fonction associée, la fonction exponentielle et la fonction de logarithme.
 La fonction connexe est un bon exemple de fonction de bijjectif. Source: F. Zapata à travers Geogebra.
La fonction connexe est un bon exemple de fonction de bijjectif. Source: F. Zapata à travers Geogebra. Les références
- Zone électronique. Types de fonctions. Récupéré de: Emathzone.com.
- Hoffman, J.g. Sélection de problèmes de mathématiques. Élégant. Spphinx.
- Les mathématiques sont amusantes. Référence des fonctions communes. Récupéré de: Mathisfun.com.
- Requena, b. Formules d'univers. Types de fonctions. Récupéré de: universoformules.com.
- Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
- « Structure iTitrio, propriétés, utilisations, obtention
- Structure Iterbio, propriétés, utilisations, obtention »


=\frac1x)
=\frac4x-3x-1)
=\frac2-x^2x^2-x-1)
=\fraccx)
)
=\sqrtx-3)
=\sqrt[3]2x^5-7)



=a\cdot&space;cosh\left&space;(\fracxa&space;\right&space;))
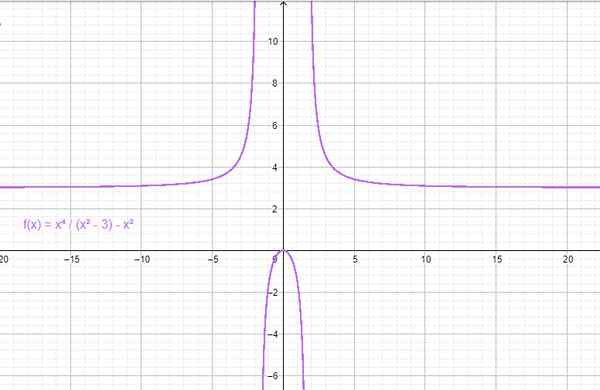
=\fracx^4x^2-3-x^2)