Tétradecágono

Qu'est-ce qu'un tétradecágono?

Le tétradecágono est une figure géométrique plate et fermée de 14 côtés, appartenant à la famille des polygones. Il est également connu sous le nom de Tetrakaidecágono, Tous les mots dérivés des mots grecs: "Tetra" (Cuatri), "Kai" (plus), "Decay" (dix) et "gon" (angle), car il a également 14 angles intérieurs.

La figure montre un tétradagon ordinaire, c'est-à-dire celui dont les côtés et les angles internes ont tous la même mesure, montrant les principales caractéristiques de cette figure.

Figure 1.- Tetrade régulière avec ses principales caractéristiques. Source: F. Zapata.

Éléments tétradecágono

• Côtés: Ils sont appelés les 14 segments de ligne qui sont fermés pour former la figure. Ils peuvent tous avoir la même longueur, auquel cas le polygone est régulier, ou ils peuvent être différents et ensuite il y a une tétrade irrégulière.
• Sommets: Ce sont les points d'intersection entre les segments successifs et le tétradecágono a 14 sommets.
• centre: Point équidistant des sommets.
• Radio: segment qui unit le centre avec un sommet.
• Angle interne: Il est formé par l'intérieur de la figure et entre deux segments successifs ou adjacents. Mesures 154.286º pour le tétradecágon ordinaire, quelle que soit la taille du côté.
• Angle externe: formé entre un côté et l'allongement de l'un des côtés adjacents. Quelle que soit la longueur latérale, cet angle mesure 25.7143º pour une tétrade ordinaire.
• Angle central: Celui qui a son sommet coïncidant avec le centre du polygone et ses côtés sont deux radios consécutives.
• Diagonale: segment qui relie deux sommets non consécutifs.

Comment est un tétradecágono?

Les polygones réguliers de n côtés qui sont construits avec la règle et la boussole ont un n de la forme 2^r p₁… P_k, Être P_Toi Fermat primo nombres différents, et à son tour les nombres premiers de Fermat prennent forme 2ⁿ + 1.

Peut vous servir: en attente de ligne: formule et équations, représentation, exemples

Le tétradecágono a n = 14 côtés, mais 14 = 7 × 2, qui ne sont pas des cousins ​​Fermat, car ils ne peuvent pas être exprimés de la manière indiquée. Par conséquent, ce polygone n'admet pas la construction exacte avec la règle et la boussole, mais une construction qui s'approche très bien, à travers plusieurs méthodes.

Méthode générale pour construire des polygones réguliers

Ce qui suit est une méthode générale (pas la seule) à construire des polygones réguliers enregistrés dans une circonférence, y compris la tétrade ordinaire.

Il consiste à diviser le diamètre vertical de cette circonférence en autant de parties égales que les côtés a le polygone pour dessiner. Dans le cas de Tetradecágono, ils seront les 14 parties numérotées dans l'image 2. Ce sont les étapes:

• Dessinez un diamètre vertical de A à B.
• Ensuite, dessinez un semi-droit à partir du point A, ouvrez la boussole avec une ouverture arbitraire et faites 14 divisions également espacées à ce sujet. Semirect et ses divisions peuvent sortir de la circonférence.
• Rejoignez la marque 14VA (en bleu dans l'image) à la fin du semi-droit avec le point B.
• Pour continuer à rejoindre le reste des marques dans le semi-réincarré avec les points respectifs sur le diamètre vertical (points verts).
• Avec la pointe de la boussole en A et l'ouverture égale à la mesure du diamètre de la circonférence, un arc est dessiné. Avec la même mesure, mais soutenant la pointe en b (point 14 de la figure 2) une autre arc est dessinée, qui est coupée avec les premiers en points v et v 'indiqué.

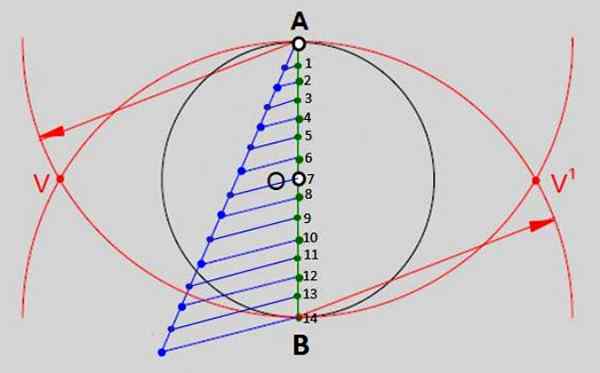Figure 2.- L'une des méthodes générales pour construire des polygones réguliers est de diviser le diamètre de la circonférence en autant de parties égales que les côtés ont le polygone. Dans le cas du tétradech ordinaire, il y a 14 parties égales. Source: F. Zapata.

• Maintenant, avec la règle, tracez une ligne de V 'au point 2 et prolongez-la pour couper la circonférence au point C de la figure 3. Marquez le point d'intersection, qui sera l'un des sommets de la figure.

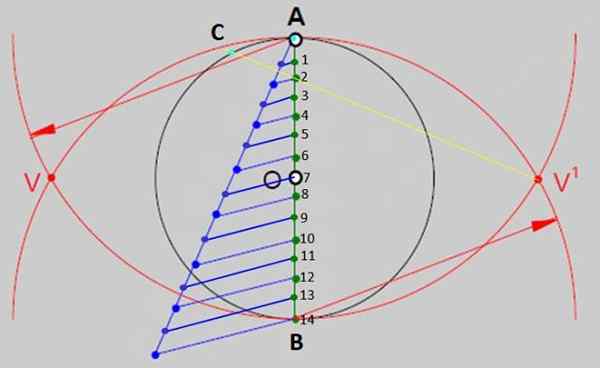Peut vous servir: branches statistiques figure 3.- Le segment AC est la mesure des côtés de la tétradécion construite. Source: F. Zapata.

• Ouvrez la boussole dans la distance CA et soutenant la pointe dans A ou C, dessinant des arcs de mesure égale sur toute la circonférence, de cette manière, il est divisé en parties approximativement égales, les intersections entre les arcs et la circonférence sont les sommets sont les sommets sont les sommets sont les sommets sont les sommets. sommets de tétradecágono.
• Avec une règle, rejoignez les sommets avec des segments de ligne, formant les côtés du polygone.
• Effacer soigneusement les constructions auxiliaires.

Dans l'animation suivante, une autre méthode approximative est affichée, avec une règle et une boussole:

Figure 4.- Animation qui montre comment un tétradecágon est fabriqué (polygone approximativement ordinaire). Source: Wikimedia Commons.

Formules pour tétrade ordinaire

Les formules suivantes sont valables pour les polygones réguliers:

• Numéro de feuille: n
• Mesure latérale: un
• Apothème: l_POUR
• Radio: R
• Périmètre: P
• Zone: A
• Angle interne: je
• Angle externe: E
• Diagonale: D

Côté connu de l'apothème

A = 2L_POUR × tg (π / n)

Pour n = 14:

A = 2L_POUR × tg (π / 14)

Côté connu de la radio

A = 2r × sen (π / n)

Oui n = 14:

A = 2r × sen (π / 14)

Périmètre connu du côté

Le périmètre est la somme des côtés. Lorsque le tétradecágono est régulier:

P = n⋅a = 14⋅a

Si le tétradecágono est irrégulier, tous les côtés doivent être ajoutés directement pour obtenir le périmètre.

Zone connue du côté

A = ¼ na² × Cot (π / n)

Pour n = 14:

A = ¼ (14e²) × cot (π / 14) = (7/2) a² × Cot (π / 14)

Zone connue

A = n⋅l_POUR ² × tg (π / n)

Prendre n = 14 résultats:

A = 14L_POUR ² × tg (π / 14)

Zone basée sur le périmètre et l'apothème

A = (p × l_POUR) / 2

Peut vous servir: Théorème de Bayes

Mesure d'angle intérieur

 Lorsque n = 14, l'angle interne du tétradecágono mesure en degrés:

I = 12 × 180º / 14 = 154.286º

Mesure d'angle externe

E = 360º / N

Quand n = 14 vous avez:

E = 25.7143º

Diagonales

La formule pour calculer le nombre de diagonales présentes dans n'importe quel polygone, régulière ou non, est:

Pour n = 14:

D = 14 × 11/2 = 77 diagonales

Exemples

Un autre exemple de tétradecágon

Les polygones réguliers apparaissent à plusieurs reprises dans de nombreuses conceptions, comme les devises. Dans le cas de la tétradagon ordinaire, cela apparaît dans les pièces commémoratives malaisiennes, représentant ses côtés à chacun des quatorze États confédérés de cette nation.

Tétradecágonc concave et convexe

En général, les polygones tels que le tétradecágono peuvent être convex ou concaves, dans le premier cas, la mesure de leurs angles internes ne dépasse pas 180º. Le tétradech ordinaire est convexe, comme tout polygone ordinaire, car l'un de ses angles internes mesure 154.286º.

D'un autre côté, dans le tétradech concave, un ou plusieurs de ses angles internes mesurent plus de 180 °.

Exemple numérique

Étant donné un tétradagon ordinaire dont le côté mesure 5 cm, trouvez: trouver:

a) périmètre
b) Mesure de l'apothéme
c) longueur radio
d) zone

Réponses

a) Comme il s'agit d'un polygone ordinaire, le périmètre est:

P = 14 × 5 cm = 70 cm.

b) de l'équation a = 2l_POUR × tg (π / 14), où a = 5 cm, l'apothem L_POUR:

L_POUR = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) La radio R peut être calculée par a = 2r × sen (π / 14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Il existe plusieurs alternatives pour la zone, par exemple a = (p × l_POUR) / 2:

A = (70 × 21.9064) / 2 cm² = 1533.45 cm².

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Géométrie arturo. Méthode générale pour dessiner des polygones inscrits aux circonférences. Récupéré de YouTube.com
3. Calculateur de soupe. Calculateur de polygone ordinaire. Récupéré de: calculatorosoup.com.
4. Dessin. Polygones réguliers. Récupéré de: dessin.com.
5. Requena, b. Polygone concave. Récupéré de: universoformules.com.
6. Wikipédia. Polygone constructible. Récupéré de: est.Wikipédia.org.