TROISIÈME APPLICATIONS, EXPÉRIMENTS ET EXERCES DE LA LOI DE NEWTON

La La troisième loi de Newton, aussi appelé Loi de l'action et de la réaction Il affirme que lorsqu'un objet exerce la force sur un autre, ce dernier exerce également sur le premier une force d'ampleur et de direction et de sens opposé.

Isaac Newton a libéré ses trois lois en 1686 dans son livre Philosophiae Naturalis Principia Mathematica ou principes mathématiques de la philosophie naturelle.

Une fusée spatiale reçoit la propulsion nécessaire grâce aux gaz expulsés. Source: Pixabay.

[TOC]

Explication et formules

La formulation mathématique de la troisième loi de Newton est très simple:

F₁₂ = -F_vingt-et-un

L'une des forces est appelée action Et l'autre est le réaction. Cependant, il est nécessaire de mettre en évidence l'importance de ce détail: les deux agissent sur différents objets. Ils le font également simultanément, bien que cette terminologie suggère à tort que l'action se produit avant et la réaction après.

Étant donné que les forces sont des vecteurs, ils indiquent avec Bold. Cette équation indique qu'il y a deux objets: objet 1 et objet 2. La force F₁₂ C'est celui qui exerce l'objet 1 sur l'objet 2. La force F_vingt-et-un est exercé par l'objet 2 sur l'objet 1. Et le signe (-) souligne qu'ils sont opposés.

Lorsque vous observez soigneusement la troisième loi de Newton, il y a une différence importante avec les deux premiers: Bien qu'ils invoquent un seul objet, la troisième loi se réfère à deux objets différents.

Et si vous pensez attentivement, les interactions nécessitent des couples d'objets.

C'est pourquoi les forces d'action et de réaction ne sont pas annulées ou équilibrées, bien qu'elles aient la même ampleur et la même direction, mais sinon: elles sont appliquées dans différents corps.

Applications

Interaction de balle - Terre

Voici une application très quotidienne d'une interaction liée à la troisième loi de Newton: une balle qui tombe verticalement et la terre. La balle tombe au sol parce que la terre exerce une force d'attraction, qui est connue sous le nom de gravité. Cette force fait tomber la balle avec une accélération constante de 9.8 m / s².

Cependant, presque personne ne pense au fait que la balle exerce également une force d'attraction sur la terre. Bien sûr, la Terre reste inaltérable, car sa masse est beaucoup plus grande que celle du ballon et éprouve donc une accélération méprisable.

Un autre problème notable concernant la troisième loi de Newton est que le contact entre les deux objets qui interagisse n'est pas nécessaire. Il est évident avec l'exemple qui vient d'être cité: le ballon ne prend toujours pas de contact avec la Terre, mais néanmoins il exerce son attraction de toute façon. Et la balle sur la terre aussi.

Une force comme gravité, qui agit de manière interchangeable à la fois s'il y a un contact entre des objets comme s'il n'y avait pas de nom de "force d'action de distance". Au lieu de cela, des forces telles que la friction et la normale exigent que les objets qui interagissent sont en contact, ils sont donc appelés "forces de contact".

Formules extraites de l'exemple

Retour aux deux objets de balle - Terre, en choisissant les taux de P pour le ballon et en T pour la Terre et en appliquant la deuxième loi de Newton à chaque participant à ce système est obtenu:

Il peut vous servir: variable discrète: caractéristiques et exemples

F_résultant = m.pour

La troisième loi stipule que:

m_Ppour_P = - m_Tpour_T

pour_P = 9.8 m / s² réalisé verticalement vers le bas. Puisque ce mouvement se déroule le long de la direction verticale peut être distribuée avec la notation vectorielle (gras); Et en choisissant la direction aussi positive et négative, vous avez:

pour_P = 9,8 m / s²

m_T ≈ 6 x 10 ²⁴ Kg

Quelle que soit la masse du ballon, l'accélération de la terre est nul. C'est pourquoi il est observé que la balle tombe vers la terre et non vice versa.

Fonctionnement d'une fusée

Les Rockets constituent un bon exemple d'application de la troisième loi de Newton. La fusée illustrée dans l'image au début s'élève grâce à la propulsion du gaz chaud à grande vitesse.

Beaucoup croient que cela se produit parce que ces gaz "soutiennent" l'atmosphère ou sur le sol pour soutenir et pousser la fusée. Ça ne marche pas comme ça.

Alors que la fusée exerce une résistance aux gaz et les expulse, les gaz exercent une force sur la fusée, qui a le même module, mais la direction opposée. Cette force est celle qui offre à la fusée son accélération.

Si vous n'en avez pas à la main une fusée, il existe d'autres moyens de vérifier que la troisième loi de Newton fonctionne pour assurer la propulsion. Des roquettes à eau peuvent être construites, dans lesquelles la poussée nécessaire est offerte par l'eau par gaz de pression.

Il convient de noter que le début d'une fusée à eau prend du temps et nécessite de nombreuses précautions.

Utilisation des patins

Un moyen plus abordable et immédiat de vérifier l'effet de la troisième loi de Newton est de mettre quelques patins et de promouvoir un mur.

La plupart du temps, la capacité d'exercer de la force avec des objets en mouvement est associé, mais la vérité est que les objets immobiles peuvent également exercer une force. Le patineur est repoussé grâce à la force que le fait que l'immature exerce dessus.

Les surfaces de contact exercent les forces de contact (normales) les unes avec les autres. Lorsqu'un livre est pris en charge sur une table horizontale, elle exerce une force verticale normale dessus. Le livre exerce sur la table une force verticale de la même valeur numérique et du sens opposé.

Expérience pour enfants: patineurs

Les enfants et les adultes peuvent vivre la troisième loi de Newton et vérifier que les forces d'action et de réaction ne sont pas annulées et sont en mesure de fournir des mouvements.

Deux patineurs sur la glace ou sur une surface très lisse peuvent être propulsés chacun.

Considérez deux patineurs avec une pâte assez différente. Ils sont au milieu d'une patinoire avec une friction méprisable et sont initialement au repos. Dans un instant donné, ils se poussent mutuellement en appliquant une force constante avec la paume des mains. Comment se déplacera les deux?

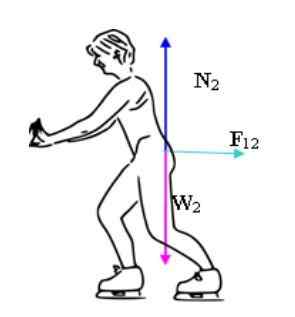
Peut vous servir: équilibrage vecteur: calcul, exemples, exercicesDeux patineurs sont propulsés au milieu d'une patinoire. Source: Benjamin Crowell (utilisateur de Wikipedia Bcrowell) [CC BY-SA 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Il est important de souligner que comme il s'agit d'une surface sans frottement, les seules forces déséquilibrées sont les forces que les patineurs s'appliquent. Alors que le poids et la normale agissent sur les deux, ces forces sont équilibrées, de ce que les patineurs accélèrent dans une direction verticale.

Formules appliquées dans cet exemple

La troisième loi de Newton déclare que:

F₁₂ = -F_vingt-et-un

C'est-à-dire que la force exercée par le patineur 1 sur le 2, est la même ampleur à laquelle les 2 exercent sur le 1, avec la même direction et la direction opposée. Notez que ces forces sont appliquées à différents objets, de la même manière que les forces étaient sur la balle et la terre dans l'exemple conceptuel précédent.

m₁ pour₁ = -m₂ pour₂

Étant donné que les forces sont opposées, les accélérations qui provoqueront également, mais leurs amplitudes seront différentes, car chaque patineur a une masse différente. Regardons l'accélération acquise par le premier patineur:

Si la masse du premier patineur est supérieure à celle de la seconde, son accélération sera inférieure. C'est à prévoir car il a une plus grande inertie. Le patineur le plus léger accélère une plus grande accélération. Si les masses sont les mêmes, les accélérations seront également.

Ainsi, le mouvement qui se produit ci-dessous est la séparation des deux patineurs dans les sens opposés. En principe, les patineurs étaient au repos au milieu de la piste. Chacun exerce une force sur l'autre qui fournit une accélération pendant que les mains sont en contact et que la poussée dure.

Après cela, les patineurs s'éloignent les uns des autres avec un mouvement rectiligne uniforme, en n'agissant pas de forces déséquilibrées. La vitesse de chaque patineur sera différente si leurs masses sont également.

Exercice résolu

Pour résoudre les problèmes dans lesquels les lois de Newton doivent être appliquées, il est nécessaire de tirer soigneusement les forces qui agissent sur l'objet. Ce dessin est appelé "diagramme du corps libre" ou "diagramme du corps isolé". Dans ce diagramme, les forces que le corps exerce sur d'autres objets ne doit pas être montrée.

S'il y a plus d'un objet impliqué dans le problème, c'est nécessaire.

1- Les patineurs de la section précédente ont des masses respectives m₁ = 50 kg et m₂ = 80 kg. Ils se poussent mutuellement avec une force constante de 200 N. La poussée a une durée de 0.40 secondes. Trouver:

a) l'accélération acquise par chaque patineur grâce à la poussée.

b) la vitesse de chacun lorsqu'elle se sépare

Solution

a) Prenez comme une adresse positive horizontale celle qui va de gauche à droite. L'application de la deuxième loi de Newton avec les valeurs fournies par la déclaration est:

F_vingt-et-un = m₁pour₁

D'où:

Pour le deuxième patineur:

b) Pour calculer la vitesse qu'ils transportent juste lorsqu'ils sont séparés, les équations cinématiques du mouvement rectiligne uniformément accéléré sont utilisées:

Peut vous servir: inductance mutuelle: formule / coefficient, applications, exercices

La vitesse initiale est de 0, car ils étaient au repos au milieu de la piste:

V_F =

V_F1 = A₁t = -4 m / s² . 0.40 S = -1.6 m / s

V_F2 = A₂T = +2.5 m / s² . 0.40 s = +1 m / s

Résultats

Comme prévu, la personne 1 étant plus légère acquiert une plus grande accélération et donc une vitesse plus rapide. Observez maintenant ce qui suit sur le produit de la pâte en raison de la vitesse de chaque patineur:

m₁ V₁ = 50 kg . (-1.6 m / s) = - 80 kg.SP

m₂ V₂ = 80 kg . 1 m / s = +80 kg.SP

La somme des deux produits est 0. Le produit de la masse par vitesse est appelé la quantité de mouvement p. C'est un vecteur avec la même direction et le même sens de la vitesse. Lorsque les patineurs étaient au repos et leurs mains en contact, on pourrait supposer qu'ils formaient le même objet dont la quantité de mouvement était:

P_soit = (m₁ +m₂) V_soit = 0

Une fois la poussée terminée, la quantité de mouvement du système de patinage reste 0. Par conséquent, la quantité de mouvement est préservée.

Exemples de la troisième loi de Newton dans la vie quotidienne

Marcher

La marche est l'une des actions les plus quotidiennes qui peuvent être effectuées. S'il est soigneusement observé, l'action de marche nécessite de pousser le pied contre le sol, de sorte qu'elle renvoie une force égale et opposée sur le pied du marcheur.

Quand nous avons constamment appliqué la troisième loi de Newton. Source: Pixabay.

C'est précisément cette force qui permet aux gens de marcher. Sur le vol, les oiseaux exercent une force dans l'air et l'air pousse les ailes afin que l'oiseau soit poussé vers l'avant.

Mouvement d'une voiture

Dans une voiture, les roues exercent une résistance sur le trottoir. Grâce à la réaction de la chaussée, il exerce sur les forces de pneu qui font avancer la voiture.

sport

Dans la pratique du sport, les forces d'action et de réaction sont nombreuses et ont une participation très active.

Par exemple, voyons l'athlète avec le pied soutenu par un bloc de démarrage. Le bloc offre une force normale en réaction à la poussée que l'athlète exerce dessus. Le résultat de cette normale et du poids du couloir, entraîne une force horizontale qui permet à l'athlète de progresser.

L'athlète utilise le bloc de démarreur pour ajouter l'impulsion vers l'avant à la sortie. Source: Pixabay.

Tuyaux de feu

Un autre exemple dans lequel la troisième loi de Newton est présente est dans les pompiers qui détiennent des tuyaux de feu. L'extrémité de ces gros tuyaux a une poignée sur la buse que le pompier doit tenir lorsque le jet d'eau sort, pour éviter le revers qui se produit lorsque l'eau sort à pleine vitesse.

Pour la même raison, c'est pratique.

Les références

1. Giancoli, D.  2006. Physique: principes avec applications. Sixième édition. Prentice Hall. 80 - 82.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson. 73 - 75.
3. Tipler, P. 2010. Physique. Volume 1. 5e édition. Éditorial Revered. 94 - 95.
4. Stern, D. 2002. Astronomes aux astronaves. Tiré de: PWG.GSFC.pot.Gouvernement.