Troisième loi des formules de thermodynamique, équations, exemples

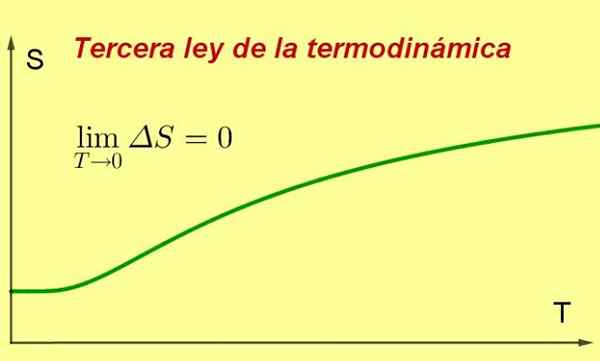
La Troisième loi de la thermodynamique indique que l'entropie d'un système thermodynamique fermé en équilibre a tendance à être minime et constante, à mesure que sa température approche 0 Kelvin.

Cette valeur de l'entropie sera indépendante des variables du système (la pression ou le champ magnétique appliqué, entre autres). Ce qui se passe, c'est que lorsque la température est plus proche de 0 K, les processus du système sont arrêtés et comment l'entropie est une mesure de l'agitation interne, elle descend nécessairement.

Figure 1. Alors que la température d'un système s'approche du zéro absolu, son entropie atteint une valeur minimale et constante. Source: Préparé par F. Zapata ..

[TOC]

Concepts précédents

Pour comprendre la portée de la troisième loi de la thermodynamique, pertinente pour les températures très basses, il est nécessaire de revoir les concepts suivants:

Système thermodynamique

Il se réfère généralement à un gaz, un liquide ou un solide. Ce qui ne fait pas partie du système est appelé autour. Le système thermodynamique le plus courant est le gaz idéal, qui se compose de n particules (atomes) qui n'interagissent que par des collisions élastiques.

Systèmes isolés, fermés ou ouverts

Les systèmes isolés ne sont autorisés aucun échange avec l'environnement. Les systèmes fermés n'échangent pas la matière avec l'environnement mais la chaleur. Enfin, les systèmes ouverts peuvent échanger à la fois la matière et la chaleur avec l'environnement.

Macro-state et microstat

Le macro-État d'un système est l'ensemble de valeurs qui ont ses variables: pression, température, volume, nombre de moles, entropie et énergie interne. D'un autre côté, l'estime micro-estime dans le cas d'un gaz idéal - est donné par la position et l'élan de chacune des n particules qui le ralentissent, à un certain moment. 

De nombreux microstats peuvent entraîner la même macro-État. Dans un gaz à température ambiante, le nombre de microstats possibles est immense, car le nombre de particules qui le représentent, les différentes positions et les différentes énergies qu'ils peuvent adopter est très grande. 

Formules et équations

L'entropie comme nous l'avons dit est une variable macroscopique thermodynamique qui mesure le système de trouble moléculaire du système. Le degré de désordre d'un système est plus grand dans la mesure où le nombre de microstats possibles est plus élevé. 

Ce concept est nécessaire pour formuler la troisième loi de la thermodynamique sous forme mathématique. Que ce soit l'entropie du système, alors:

Cela signifie que l'entropie s dans un système fermé ne change pas lorsque sa température t a tendance à zéro absolu.

L'entropie est une variable d'état macroscopique qui est directement liée au nombre de microstate possible d'un système, au moyen de la formule suivante:

S = k ln (w)

Dans l'équation précédente: S représente l'entropie, W le nombre de microstats possibles du système et k C'est la constante de Boltzmann (K = 1.38 x 10^-23 J / k). C'est-à-dire que l'entropie d'un système est k fois le logarithme naturel du nombre de microstats possibles.

Calcul de l'entropie absolue d'une substance

Il est possible de définir l'entropie absolue d'une substance pure basée sur la définition de la variation de l'entropie:

Où Δq est la variation infinitésimale de la chaleur et t est la température. Cette équation est valable si le processus est réversible (Rev).S'il s'agit d'un processus de pression constant isobare, la chaleur échangée lors d'une variation de température infinitésimale peut être écrite comme ceci:

Δq = n . c_p .Dt

Ici CP est la chaleur molaire spécifique et n le nombre de moles. La dépendance à la chaleur spécifique molaire avec la température est un fait obtenu expérimentalement et connu pour de nombreuses substances pures.

Peut vous servir: Système solaire: planètes, caractéristiques, origine, évolution

Selon la troisième loi en substances pures: 

Alors le entropie absolue d'une mol de substance pure comme:

Dans la notation précédente, la barre indique qu'il s'agit de l'entropie d'une mol de substance et que le suerson º dénote une substance pure.

Applications

Dans la vie quotidienne, la troisième loi de la thermodynamique a peu d'applications, assez contrairement à la première et deuxième loi. C'est parce que c'est un principe qui fait référence à ce qui se passe dans un système lorsqu'il aborde le 0, un rang de températures rares.

En fait, atteindre l'absolu ou −273,15 ° C est impossible (voir l'exemple 1 plus tard) cependant, la troisième loi est appliquée lors de l'étude de la réponse des matériaux à des températures très basses. 

Grâce à cela, des progrès importants dans la matière condensée ont émergé, comme:

-Superfluidité (voir l'exemple 2 plus tard)

-Supraconductivité 

-Techniques de refroidissement au laser 

-Condensat de Bose-Einstein 

-Gaz superflues Fermi.

Figure 2. Hélium liquide superflu. Source: Wikimedia Commons.

À des températures extrêmement basses, la descente de l'entropie permet l'émergence de phénomènes quantiques intéressants. Par conséquent, voyons ce qui se passe avec l'entropie d'un système à très basse température.

Entropie d'un système à basse température

Lorsque vous avez une substance cristalline parfaite, son entropie minimale est exactement nulle, car c'est un très bien rangé. Dans des températures proches de 0 absolue, la matière est à l'état condensé (liquide ou solide) et les vibrations en verre sont minimes.

Certains auteurs considèrent une énoncé alternatif de la troisième loi de la thermodynamique suivante:

"Si la matière se condense en formant un cristal parfait, lorsque la température a tendance à zéro absolue, l'entropie tend exactement à zéro". 

Punchons certains aspects de la déclaration précédente: 

- Un cristal parfait est celui dans lequel chaque molécule est identique et dans laquelle la structure moléculaire est répétée de manière identique dans son intégralité.

- Comme la température a tendance à zéro absolue, les vibrations atomiques diminuent presque complètement.

Ensuite, le verre forme une seule configuration possible ou micro-statement, c'est-à-dire W = 1, Et donc l'entropie est égale à zéro:

 S = k ln (1) = 0

Mais pas aussi longtemps qu'un matériau refroidi près du zéro absolu forme un cristal, encore moins ce cristal est parfait. Cela ne se produit que si le processus de refroidissement est très lent et réversible.

Sinon, des facteurs tels que les impuretés présents dans le verre rendraient possible l'existence d'autres microstats. Donc w> 1 et l'entropie serait supérieure à 0.

Entropie résiduelle

Si le processus de refroidissement est brusque, pendant la même chose, le système passe par une succession d'états de non-équation, ce qui conduit au matériel à montrer. Dans ce cas, il n'y a pas de structure cristalline et ordonnée, mais un solide amorphe, dont la structure est similaire à celle d'un liquide. 

Dans ce cas, la valeur d'entropie minimale à proximité du zéro absolu n'est pas nulle, car le nombre de microstats est bien supérieur à 1. La différence entre cette entropie et l'entropie nulle de l'état cristallin parfait est connue sous le nom de entropie résiduelle.

L'explication est qu'en dessous d'une certaine température de seuil, le système n'a pas d'autre possibilité que d'occuper.

Il peut vous servir: Première loi de la thermodynamique: formules, équations, exemples

Ils seront responsables du maintien d'une entropie constante, même si la température continue de descendre vers un zéro absolu.

Exemples

Exemple 1: Le zéro absolu et l'indétermination de Heisenberg

Le principe de l'indétermination de Heisenberg établit que l'incertitude dans la position et l'élan d'une particule, par exemple dans les atomes d'un réseau cristallin, n'est pas indépendante de l'autre, mais suivez l'inégalité suivante:

Δx ⋅ Δp ≥ H

Où h est la constante de Planck. C'est-à-dire que l'incertitude dans la position multipliée par l'incertitude dans l'élan (masse par vitesse) est supérieure ou égale à la constante de Planck, dont la valeur est très petite, mais pas nulle: H = 6.63 x 10-3. 4 J · S.

Et qu'est-ce que le principe de l'incertitude a à voir avec la troisième loi de la thermodynamique? Si la position des atomes du réseau cristallin est fixe et précise (Δx = 0) Ensuite, la vitesse de ces atomes peut prendre n'importe quelle valeur entre 0 et l'infini. Ceci est contredit par le fait que dans le zéro absolu, chaque mouvement de l'agitation thermique cesse.

Réciproquement, si nous commençons cela à un zéro de température absolue, toute l'agitation cesse et l'élan de chaque atome du réseau est exactement zéro (Δp = 0), alors le principe de l'incertitude de Heisenberg impliquerait que l'indétermination dans les positions de chaque atome serait infinie, c'est-à-dire qu'ils peuvent être dans n'importe quelle position. 

À la suite de l'énoncé précédent, le nombre de microstats tendrait à l'infini et à l'entropie prendrait également une valeur indéterminée. 

Exemple 2: Superfluidité et l'étrange cas d'hélium-4

Dans la superfludité, qui se produit à des températures très basses, la matière perd la friction interne entre ses molécules, appelée gelée. Dans ce cas, le liquide pourrait circuler sans frottement pour toujours, mais le problème est à ces températures presque rien n'est liquide sauf l'hélium.

L'hélium et l'hélium 4 (son isotope le plus abondant) constituent un cas unique, car à la pression atmosphérique et à des températures proches du zéro absolu, l'hélium reste liquide. 

Lorsque l'hélium-4 est soumis à une température inférieure à 2.2 k à la pression atmosphérique devient un superflu. Cette découverte s'est produite en 1911 à Leyden par le physicien néerlandais Heike Kamerlingh Onnes (1853-1926).

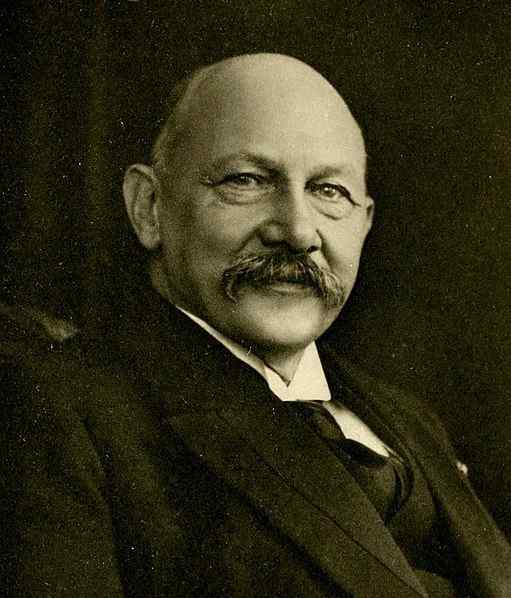figure 3. Physicien néerlandais Heike Kamerlingh Onnes (1853-1926). Source: Wikimedia Commons.

L'atome Helio-4 est un Bosison. Les bosons, contrairement aux fermions, sont des particules qui peuvent occuper tout le même état quantique. Par conséquent, les bosons ne répondent pas au principe d'exclusion de Pauli.

Puis tous les atomes d'hélium-4 à des températures inférieures à 2.2 k occupe le même état quantique et il n'y a donc rien de plus qu'un seul microstate possible, ce qui implique que l'hélium-4 superflu a s = 0.

Exercices résolus

- Exercice 1

Considérez un cas simple composé d'un système formé uniquement par trois particules qui ont trois niveaux d'énergie. Pour ce système simple:

a) Déterminer le nombre de microstate possible pour trois plages de température:

-haut 

-Moitié 

-Faible

b) Déterminer à travers l'entropie de l'équation de Boltzmann dans les différentes gammes de température. 

c) Discutez des résultats et expliquez s'il faut contredire la troisième loi de la thermodynamique.

Solution à

Sur une échelle moléculaire et atomique, les énergies qu'un système peuvent adopter sont quantifiées, ce qui signifie que seules certaines valeurs discrètes peuvent prendre. De plus, lorsque les températures sont si faibles, les particules qui composent le système n'ont que la possibilité d'occuper moins de niveaux d'énergie. 

Il peut vous servir: induction magnétique: formules, comment elle est calculée et des exemples

Température haute

Si le système a une température relativement élevée, les particules ont suffisamment d'énergie pour occuper tous les niveaux disponibles, donnant naissance à 10 microstats possibles, qui apparaissent dans la figure suivante:

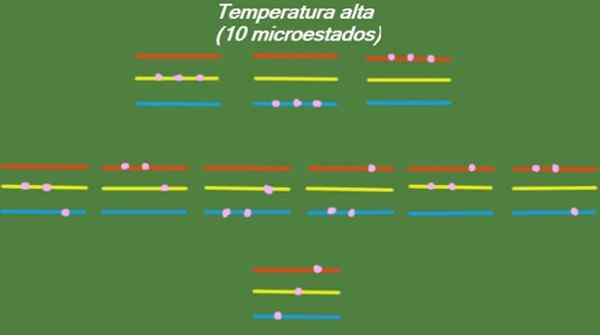Figure 4. États possibles à haute température pour l'année résolus 1. Source: Préparé par F. Zapata.

Température moyenne

Dans le cas où le système possède une température intermédiaire, les particules qui le composent n'ont pas assez d'énergie pour occuper le plus haut niveau d'énergie. Les microstats possibles sont illustrés sur la figure:

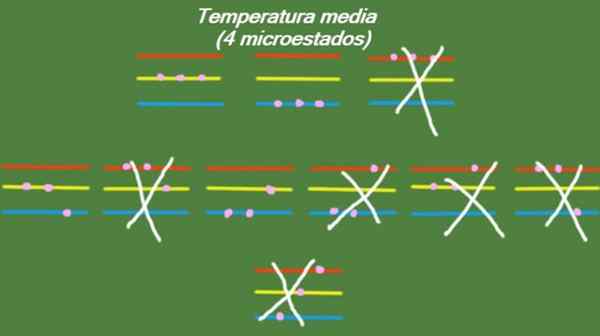Figure 5. Micro-État à température moyenne pour le système d'exercice résolu 1. Source: Préparé par F. Zapata.

Basse température

Si la température continue de descendre dans nos trois particules idéalisées et trois niveaux d'énergie, les particules auront si peu d'énergie qu'elles ne peuvent occuper que le niveau le plus bas. Dans ce cas, il n'y a qu'un seul microstate possible, comme on peut le voir dans la figure 6:

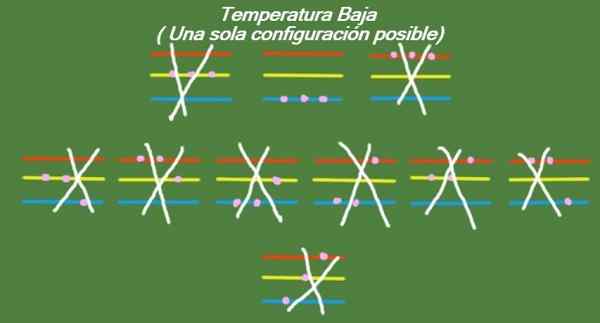Figure 6. À basse température, il y a une configuration possible (propre élaboration)

Solution B

Déjà connu le nombre de microstats dans chaque plage de température, nous pouvons déjà utiliser l'équation de Boltzmann donnée précédemment pour trouver l'entropie dans chaque cas.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J / k (Température haute)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J / k (Température moyenne)

Et finalement:

S = k ln (1) = 0 (Basse température)

Solution C

En premier lieu, nous remarquons que l'entropie diminue à mesure que la température descend, comme prévu. Mais pour les valeurs de température les plus basses, une valeur de seuil est atteinte, à partir de laquelle l'état de base du système est atteint.

Même si la température est aussi proche que possible à Absolute Zero, il n'y a pas d'états plus petits disponibles. Entropie maintient alors sa valeur minimale constante, qui dans notre exemple est s = 0.

Cet exercice illustre, au niveau des microstats d'un système, la raison pour laquelle la troisième loi de la thermodynamique est remplie.

- Exercice 2

Raison si l'instruction suivante est vraie ou fausse:

"L'entropie d'un système à la température absolue zéro est exactement zéro".

Justifier la réponse et décrire quelques exemples.

Solution

La réponse est: fausse.

Tout d'abord, la température absolue ne peut être atteinte car le principe d'incertitude de Heisenberg et de la troisième loi de la thermodynamique serait violé. 

Il est très important d'observer que dans la troisième loi, il n'est pas dit ce qui se passe dans l'Absolu 0, mais lorsque la température est infiniment proche de l'Absolu 0. La différence est subtile, mais significative.

La troisième loi n'affirme pas que lorsque la température prend une valeur arbitrairement près de Zero absolu, l'entropie tend à zéro. Cela ne se produirait que dans le cas précédemment analysé: le cristal parfait, qui est une idéalisation.

De nombreux systèmes à échelle microscopique, c'est-à-dire à l'échelle quantique, ont leur niveau de base d'énergie dégénérer, Ce qui signifie l'existence de plusieurs configurations au niveau d'énergie le plus bas. 

Ce qui précède signifie que dans ces systèmes, l'entropie ne serait jamais exactement nul. L'entropie ne serait pas non plus exactement nulle dans les systèmes qui sont vitrifiés lorsque la température a tendance à zéro absolu. Dans ce cas, le entropie résiduelle Avant de voir.

C'est parce que leurs molécules étaient "coincées" avant d'occuper les niveaux d'énergie les plus bas disponibles, ce qui augmente considérablement le nombre de microstats possibles, ce qui rend impossible que l'entropie soit exactement zéro.

Les références

1. Cengel, et. 2012. Thermodynamique. 7e édition. McGraw Hill. 347.
2. Laboratoire de propulsion à réaction. L'endroit le plus cool de l'univers. Récupéré de: ColdatomLab.JPL.pot.Gouvernement.
3. González, un. Entropie et spontanéité. Récupéré de: Géocités.WS
4. Quora. Quelle est l'utilisation pratique de la troisième loi de la thermodynamique?. Récupéré de: Quora.com
5. Chimie générale. Troisième principe de la thermodynamique. Récupéré de: Corinthe.PUCP.Édu.pe
6. Troisième loi de la thermodynamique. Récupéré de: youtube.com
7. Wikipédia. Résidu d'entropie. Récupéré de: dans.Wikipédia.com
8. Wikipédia. Troisième loi de la thermodynamique. Récupéré de: dans.Wikipédia.com