Théorème de l'existence et de la démonstration de l'unicité, des exemples et des exercices

Il Théorème d'existence et d'unicité établit les conditions nécessaires et suffisantes pour une équation différentielle de premier ordre, avec une condition initiale donnée, pour avoir une solution et que cette solution est également la seule. 

Cependant, le théorème ne donne aucune technique ou indication de la façon de trouver une telle solution. Le théorème de l'existence et de l'unicité s'étend également à des équations différentielles d'ordre supérieur avec des conditions initiales, qui est connue sous le nom de problème de Cauchy.

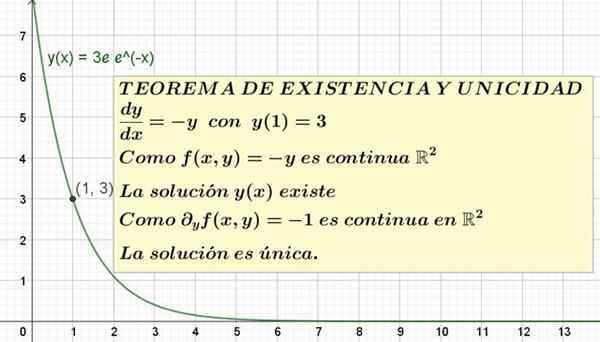
Figure 1. Une équation différentielle avec l'état initial et sa solution est montrée. Le théorème de l'existence et de l'unicité garantit que c'est la seule solution possible.

L'énoncé officiel du théorème de l'existence et de l'unicité est le suivant:

"Pour une équation différentielle et '(x) = f (x, y) avec condition initiale et (a) = b,  Ça existe au moins une solution dans une région rectangulaire de l'avion Xy contenant le point (UN B), Ouais f (x, y) C'est continu dans cette région. Et si le dérivé partiel de F à l'égard de et: G = ∂f / ∂y Il est continu dans cette même région rectangulaire, donc la solution est unique dans un environnement du point (UN B) Contenu dans la région de continuité de F et g."

L'utilité de ce théorème réside d'abord pour savoir quelles sont les régions du plan XY dans lesquelles il peut y avoir une solution et savoir si la solution trouvée est la seule possible ou s'il y en a d'autres. 

Notez que dans le cas où la condition de.

[TOC]

Démonstration de l'existence et du théorème de l'unicité

Figure 2. À Charles Émile Picard (1856-1941) L'une des premières manifestations du théorème de l'existence et de l'unicité est accrédité. Source: Wikimedia Commons.

Pour ce théorème, deux démonstrations possibles sont connues, l'une d'entre elles est la démonstration de Charles Émile Picard (1856-1941) et l'autre est due à Giuseppe Peano (1858-1932) sur la base des travaux d'Augustin Louis Cauchy (1789-1857 ).

Peut vous servir: vecteurs simultanés: caractéristiques, exemples et exercices

Il convient de noter que les esprits mathématiques les plus brillants du XIXe siècle ont participé à la démonstration de ce théorème, il peut donc être intui.

Pour démontrer officiellement le théorème, il est nécessaire d'établir d'abord une série de concepts de mathématiques plus avancés, tels que les fonctions de type Lipschitz, les espaces de Banach, le caratheodory et plusieurs théorèmes plus existence, qui échappent au but de l'article.

Une grande partie des équations différentielles gérées en physique traite des fonctions continues dans les régions d'intérêt, nous nous limiterons donc à montrer la façon dont le théorème est appliqué dans des équations simples.

Exemples

- Exemple 1

Considérez l'équation différentielle suivante avec une condition initiale:

et '(x) = - y; avec et (1) = 3

Y a-t-il une solution pour ce problème? Est-ce la seule solution possible?

Réponses

Premièrement, l'existence de la solution de l'équation différentielle est évaluée et qu'elle répond également à la condition initiale. 

Dans cet exemple f (x, y) = - y L'état d'existence nécessite de savoir si  f (x, y) Il est continu dans une région plane Xy contenant le point de coordonnées x = 1, y = 3.

Mais f (x, y) = -y C'est le fonction connexe, qui est continu dans le domaine des nombres réels et existe dans toute la gamme de nombres réels.

Par conséquent, il est conclu que f (x, y) est continu en r², Le théorème garantit donc l'existence d'au moins une solution.

Sachant cela, il est temps d'évaluer si la solution est unique ou si au contraire il y a plus d'un. Pour cela, il est nécessaire de calculer le dérivé partiel de F Concernant la variable et:

∂f / ∂y = ∂ (-y) / ∂y = -1

Ensuite G (x, y) = -1 qui est une fonction constante, qui est également définie pour tous² Et c'est aussi continu là-bas. Il s'ensuit que l'existence et le théorème de l'unicité garantissent que ce problème de valeur initiale a une solution unique, bien qu'elle ne nous dise pas ce qu'elle est.

Peut vous servir: polygone convexe: définition, éléments, propriétés, exemples

- Exemple 2

Considérez l'équation différentielle ordinaire du premier ordre suivant avec l'état initial:

et '(x) = 2√y; et (0) = 0.

Y a-t-il une solution et (x) pour ce problème? Si c'est le cas, déterminez s'il y en a un ou plusieurs.

Répondre

Nous considérons la fonction f (x, y) = 2√y. La fonction F est défini uniquement pour y≥0, Eh bien, nous savons qu'un nombre négatif manque de racine réelle. En outre f (x, y) Il est continu dans le semi-coulain supérieur de r²  y compris l'axe x, donc L'existence et le théorème de l'unicité garantissent Au moins une solution dans cette région.

Maintenant, la condition initiale x = 0, y = 0 est au bord de la région de la solution. Ensuite, nous prenons la dérivée partielle de f (x, y) par rapport à y:

∂f/ ∂y = 1 / √y

Dans ce cas, la fonction n'est pas définie pour y = 0, précisément où la condition initiale est.

Ce qui nous dit le théorème? Il nous dit que bien que nous sachions qu'il existe au moins une solution le semi-couloir supérieur de l'axe x, y compris l'axe x, car l'état de l'unicité n'est pas rempli, il n'y a aucune garantie qu'il existe une seule solution.

Cela signifie qu'il pourrait y avoir une ou plusieurs solutions dans la région de continuité de F (x, y). Et comme toujours, le théorème ne nous dit pas ce qui pourrait être.

Exercices résolus

- Exercice 1

Résolvez le problème du Cauchy de l'exemple 1:

et '(x) = - y; avec et (1) = 3. 

Trouvez la fonction y (x) qui satisfait l'équation différentielle et la condition initiale.

Solution

Dans l'exemple 1, il a été déterminé que ce problème a une solution et est également unique. Pour trouver la solution, la première chose qui doit être remarquée est qu'il s'agit d'une équation différentielle de premier degré de variables séparables, qui est écrite comme suit:

Peut vous servir: coefficient de variation: à quoi sert-il, calcul, exemples, exercices

dy / dx = - et → dy = -y dx

Diviser entre et dans les deux membres pour séparer les variables que nous avons:

dy / y = - dx

Une intégrale indéfinie dans les deux membres est appliquée:

∫ (1 / y) dy = - ∫dx

La résolution des intégrales indéfinies est:

ln (y) = -x + c

où c est une constante d'intégration déterminée par la condition initiale:

ln (3) = -1 + c, c'est-à-dire que c = 1 + ln (3)

Le remplacement de la valeur de C et de la réorganisation est:

ln (y) - ln (3) = -x + 1

Application des propriétés suivantes des logarithmes:

La différence de logarithmes est le quotient logarithme

L'expression précédente peut être réécrite comme ceci:

ln (y / 3) = 1 - x

La fonction exponentielle est appliquée auprès des deux membres pour obtenir:

Y / 3 = e^{(1 fois)}

Ce qui équivaut à:

 y = 3e e^-X

Ceci est la solution unique de l'équation et '= -y avec y (1) = 3. Le graphique de cette solution est illustré à la figure 1.

- Exercice 2

Trouvez deux solutions au problème soulevé dans l'exemple 2:

et '(x) = 2√ (y); et (0) = 0.

Solution

Il s'agit également d'une équation de variables distinctes, qui est écrite de restes différentiellement:

Dy / √ (y) = 2 dx

Prendre l'intégrale indéfini dans les deux membres Restes:

2 √ (y) = 2 x + c

Comme on sait que y≥0 Dans la région de la solution, nous avons:

y = (x + c)² 

Mais comme la condition initiale x = 0, y = 0 doit être remplie, alors la constante C est nul et la solution suivante reste:

et (x) = x².

Mais cette solution n'est pas unique, la fonction y (x) = 0 est également une solution du problème soulevé. Le théorème de l'existence et de l'unicité appliqué à ce problème dans l'exemple 2 avait déjà prédit qu'il pourrait y avoir plus d'une solution.

Les références

1. Coddington, Earl A.; Levinson, Norman (1955), Théorie des équations différentielles ordinaires, New York: McGraw-Hill.
2. Encyclopédie des mathématiques. Théorème de Cauchy-Lipschitz. Récupéré de: Encyclopediaofmath.org
3. Lindelöf, South L'A application de la méthode des approximations successives aux équations différentielles ordinaires du Premier Ordre; Compttes Rendus Hebdomadaires des Séances de L'ANC ACADEQUIE DES SCIENCES. Vol. 116, 1894, pp. 454-457. Récupéré de: gallic.BNF.frousser.
4. Wikipédia. Méthode des approches successives de Picard. Récupéré de: est.Wikipédia.com
5. Wikipédia. Théorème de Picard-Lindelöf. Récupéré de: est.Wikipédia.com.
6. Zill, D.1986. Équations différentielles élémentaires avec applications.Prentice Hall.