Théorème du Thévenin Ce qui consiste, applications et exemples

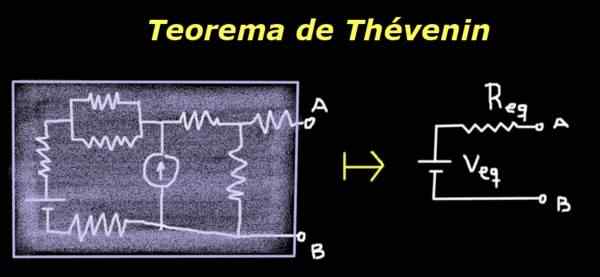
Il Théorème de la Thévénine Il indique qu'un circuit avec les bornes A et B peut être remplacé par un équivalent qui se compose d'une source et d'une résistance en série, dont les valeurs donnent la même différence de potentiel entre A et B et la même impédance que le circuit d'origine.

Ce théorème a été libéré en 1883 par l'ingénieur français Léon Charles Thévenin, mais il est affirmé qu'il avait été déclaré trente ans auparavant par le physicien allemand Hermann von Helmholtz.

Figure 1. Théorème de la Thévénine. Source: auto-faite

Son utilité réside dans le fait que, même si le circuit d'origine est complexe ou inconnu, aux fins d'une charge ou d'une impédance qui est placée entre les bornes A et B, le circuit équivalent simple de la Thévénine se comporte de la même manière que l'original.

[TOC]

Comment la tension équivalente étape par étape est-elle calculée?

La tension ou la différence de potentiel du circuit équivalent peut être obtenue de la manière suivante:

- Expérimentalement

Obtention de la tension équivalente de la Thévenin

S'il s'agit d'un appareil ou d'un équipement qui se trouve dans une «boîte noire», la différence de potentiel entre les bornes A et B avec un voltmètre ou un oscilloscope est mesurée. Il est très important qu'aucune charge ou impédance entre les bornes A et B ne soit placée. 

Un voltmètre ou un oscilloscope ne représente aucune charge pour les terminaux, car les deux équipes ont une très grande impédance (idéalement infinie) et ce serait comme si les terminaux A et B étaient sans charge. La tension ou la tension obtenue de cette manière est la tension équivalente de la Thévenin.

Obtention de l'impédance équivalente de la Thévenin

Pour obtenir l'impédance équivalente à partir d'une mesure expérimentale, une résistance connue entre les bornes A et B est placée et la chute de tension ou le signal de tension avec un oscilloscope est mesurée. 

De la chute de tension dans la résistance connue parmi les bornes, le courant qui circule à travers elle peut être obtenu. 

Le produit du courant obtenu avec la résistance équivalente plus la chute de tension mesurée dans la résistance connue est égale à la tension équivalente de la thévénine précédemment obtenue. De cette égalité, l'impédance équivalente de la Thévenin est effacée.

- Résoudre le circuit

Calcul de tension équivalent de Thévenin

Tout d'abord, toute charge ou impédance des bornes A et B est déconnectée.

Comme le circuit est connu, les mailles ou les lois de Kirchhoff sont appliquées pour trouver la tension dans les terminaux. Cette tension sera l'équivalent de Thévenin.

Peut vous servir: Mount Olympus (Mars)

Le calcul de l'impédance équivalent de Thévenin

Pour obtenir l'impédance équivalente, nous passons à:

- Remplacez les sources de tension de circuit d'origine par des circuits courts "zéro impédance" et les sources de circuit d'origine pour "Impédance infinie ouverte".

- Alors l'impédance équivalente est calculée en suivant les règles de l'impédance des séries et des impédances en parallèle.

Applications du théorème de Thévenin (partie I)

Nous appliquerons le théorème de Thévenin pour résoudre certains circuits. Dans cette première partie, nous considérons un circuit qui n'a que des sources de tension et des résistances.

Exemple 1 (calcul de la tension équivalente étape par étape)

La figure 2 montre le circuit qui se trouve dans une boîte céleste qui a deux batteries de force électromotrice V1 et V2 respectivement et les résistances R1 et R2, le circuit a les bornes A et B à laquelle une charge peut être connectée.

Figure 2. Exemple 1 du théorème de Thévenin. Source: auto-faite

L'objectif est de trouver le circuit équivalent de la Thévenin, c'est-à-dire déterminer les valeurs VT et RT du circuit équivalent.  Appliquer les valeurs suivantes: v1 = 4v, v2 = 1v, r1 = 3Ω, r2 = 6Ω et r = 1Ω.

Pas à pas

Étape 1 

Nous déterminerons la tension dans les bornes A et B lorsqu'elles ne seront pas placées.

Étape 2

Le circuit à résoudre se compose d'un seul maillage à travers lequel un courant I circule que nous avons pris positivement dans le sens des aiguilles d'une montre.

Étape 3

Nous parcourons le maillage en commençant par le coin inférieur gauche. L'itinéraire mène à l'équation suivante:

V1 - i * r1 - i * r2 - v2 = 0

Étape 4

Nous effacons le courant du maillage I et obtenons:

I = (v1 -v2) / (r1 + r2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A

Étape 5

Avec le courant de maillage, nous pouvons déterminer la tension ou la différence de tension entre A et B, qui est:

Vab = v1 - i * r1 = 4V - ⅓ a * 3Ω = 3V

C'est-à-dire que la tension équivalente de Thevenin est: vt = 3v.

Étape 6 (résistance équivalente à la Thévenin)

Nous procédons maintenant à calculer la résistance équivalente de la Thévenin, pour laquelle et comme précédemment, les sources de tension sont remplacées par un câble.

Dans ce cas, nous n'avons que deux résistance en parallèle, donc la résistance équivalente de la Thévenin est:

Rt = (r1 * r2) / (r1 + r2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω

Exemple 1b (courant de courant en utilisant l'équivalent de la Thévenin)

Connectez-vous en charge aux bornes A et B A Résistance R = 1Ω au circuit équivalent et trouvez le courant qui circule à travers ladite charge. 

Peut vous servir: mouvement rectiligne: caractéristiques, types et exemples

Solution

Lorsque la résistance R est connectée au circuit équivalent de Thevenin, il y a un circuit simple qui se compose d'une source de VT une résistance en série en série avec résistance R. 

Nous appellerons le courant qui circule à travers la charge R, afin que l'équation du maillage soit comme ceci:

Vt - ic * rt - ic * r = 0

À partir de laquelle il s'ensuit que le CI est donné par:

Ic = vt / (rt + r) = 3v / (2Ω + 1Ω) = 1 a

Vérification du théorème de la Thévénine

Pour vérifier que le théorème de Thévenin est rempli, connectez R au circuit d'origine et trouvez le courant qui circule en appliquant la loi des maillages au circuit résultant.

Le circuit résultant reste et ses équations en maillage sont comme indiqué dans la figure suivante:

figure 3. Courants de maillage. (Élaboration propre)

Ajout des équations de maillage, il est possible de trouver le courant de maillage I1 en fonction du courant I2. Ensuite, il est remplacé dans la deuxième équation de maillage et il y a une équation avec I2 comme seule inconnue. Le tableau suivant montre les opérations.

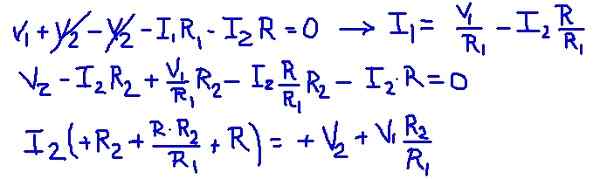Figure 4. Détail des opérations. (Élaboration propre)

Ensuite, les valeurs de résistance et les tensions des sources sont remplacées, obtenant la valeur numérique du courant de maillage i2.

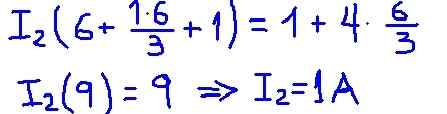Figure 5. Détail des résultats. (Élaboration propre)

Le flux I2 Mesh est le courant qui circule à travers la résistance à la charge R et la valeur trouvée à partir de 1 un coïncide entièrement avec ce qui a été trouvé précédemment avec le circuit équivalent de la Thévenin.

Application du théorème de Thévenin (partie II)

Dans cette deuxième partie, le théorème de Thévenin sera appliqué dans un circuit qui a des sources de tension, une source de courant et des résistances. 

Exemple 2A (résistance équivalente à la thénin)

L'objectif est de déterminer le circuit équivalent de la Thévenin correspondant au circuit de la figure suivante, lorsque les bornes sont sans résistance de 1 ohmio, alors la résistance est placée et que le courant est déterminé par le même.

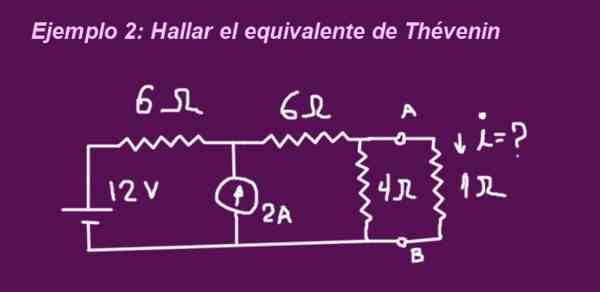Figure 6. Exemple 2 circuit. (Élaboration propre)

Solution

Pour trouver la résistance équivalente, la résistance à la charge est supprimée (dans ce cas celle de 1 ohmio). De plus, les sources de tension sont remplacées par un court-circuit et des sources de courant avec un circuit ouvert. 

De cette façon, le circuit auquel la résistance équivalente sera calculée est celle ci-dessous:

Peut vous servir: Boltzmann constant: histoire, équations, calcul, exercices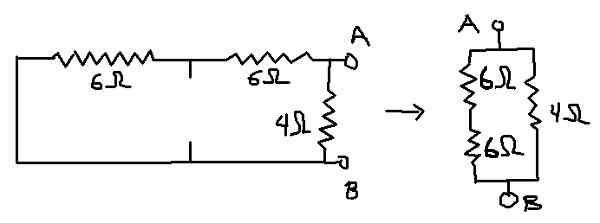Figure 7. Détail pour le calcul de la résistance équivalente (propre élaboration)

Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω qui est la résistance équivalente de la thevenin (RTH).

Exemple 2B 

Calculer la tension équivalente de Thévenin.

Solution

Pour calculer la tension équivalente de la Thévenine, nous considérons le circuit suivant, dans lequel nous placerons les courants en I1 et I2 dans les branches indiquées dans la figure suivante:

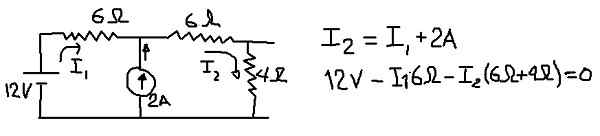Figure 8. Détails pour le calcul de la tension de la Thévenin. (Élaboration propre)

Dans la figure précédente, l'équation des nœuds de courant et l'équation des tensions sont indiqués lorsque le maillage externe est parcouru. À partir de la seconde des équations, le Current I1 est effacé:

I1 = 2 - i2 * (5/3)

Cette équation est remplacée dans l'équation des nœuds:

I2 = 2 - (5/3) i2 + 2 ===> i2 (8/3) = 4 ===> i2 = 12/8 = 1,5 A

Cela signifie que la baisse de tension en résistance à 4 ohms est de 6 volts.

Bref, la tension de Thévenin est VTH = 6 V.

Exemple 2C

Trouvez le circuit équivalent de Thevenin et Current dans la résistance à la charge.

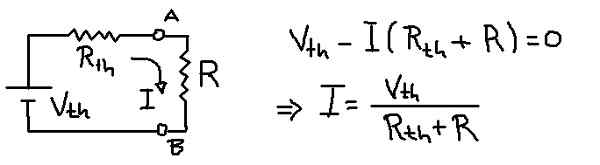Figure 9. Courant en charge avec l'équivalent de la thénin. (Élaboration propre)

Solution

La figure précédente montre le circuit équivalent de la thévénine avec la résistance à la charge r. À partir de l'équation de tension dans le maillage, le courant I qui circule à travers la résistance de charge R est déduit.

I = vth / (rth + r) = 6v / (3Ω + 1Ω) = 1,5 a

Application du théorème de Thévenin (partie III)

Dans cette troisième partie de l'application du théorème de Thévenin, un circuit de courant alternatif contient une source de tension alternative, un condenseur, l'inductance et la résistance sont considérés. 

Exemple 3

L'objectif est de trouver le circuit de Thévenin équivalent du circuit suivant:

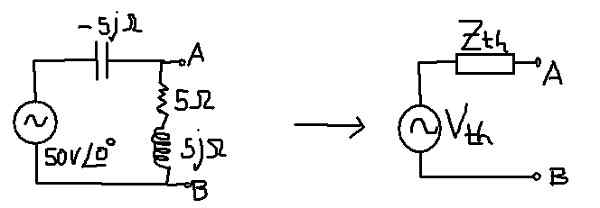Figure 10. Thévenin dans un circuit de courant alternatif. (Élaboration propre)

Solution

L'impédance équivalente correspond à celle du condenseur parallèle à la combinaison de la série de résistance et d'inductance.

L'inverse de l'impédance équivalente est donnée par:

Zeq ^ -1 = (-5J) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) J + ((1/10 + (1/10) J) = (1/10 + 3 / 10 J) MHO

Et l'impédance équivalente sera alors:

Zeq = (1 - 3 j) ohm

Le courant complexe I peut être déduit de l'équation du maillage:

50V∠0 - I (-5 J + 5 + 5J) = 50V∠0 - i * 5 = 0 ===> i = 10a ∠0 

Maintenant, la chute de tension dans la résistance et l'inductance sont calculées, c'est-à-dire la tension VAB qui sera la tension équivalente de la Thévenin:

Vab = i * (5 + 5 j) ω = 10a ∠0 * 5Ω∠45º = 50v∠45º

Autrement dit

Les références

1. Tutoriels électroniques, théorème de Thevenin. Récupéré de: électronique-Tormales.WS
2. Questions et réponses de la théorie du réseau. Théorème de Thevenin. Récupéré de: Sanfoundry.com
3. Théorème de Thevenin. Procédure étape par étape. Récupéré de: ElectricTechnology.org
4. Théorème de Thevenin. Exemple résolu étape par étape. Récupéré de: ElecticalSimple.Blogspot.com
5. Atelier sur les théorèmes de Thevenin et Norton. Récupéré de: Web.iit.Édu
6. Wikipédia. Théorème de la Thévénine. Récupéré de: Wikipedia.com