Théorème de Lamy

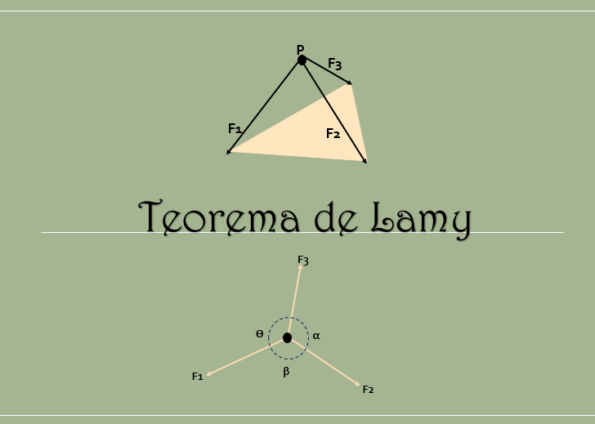
Le théorème de Lamy établit que lorsqu'un corps rigide est en équilibre et à l'action de trois forces de couple (forces qui se trouvent dans le même plan), leurs lignes d'action concordent au même point.

Le théorème a été déduit par le physicien français et religieux. Il est largement utilisé pour trouver la valeur d'un angle, la ligne d'action d'une force ou pour former le triangle des forces.

Explication

Le théorème établit que pour que l'état de l'équilibre soit rempli, les forces doivent être des coplanares; c'est-à-dire que la somme des forces exercées sur un point est nulle.

De plus, comme on le voit dans l'image suivante, il est accompli qu'en prolongeant les lignes d'action de ces trois forces, elles s'accordent au même point.

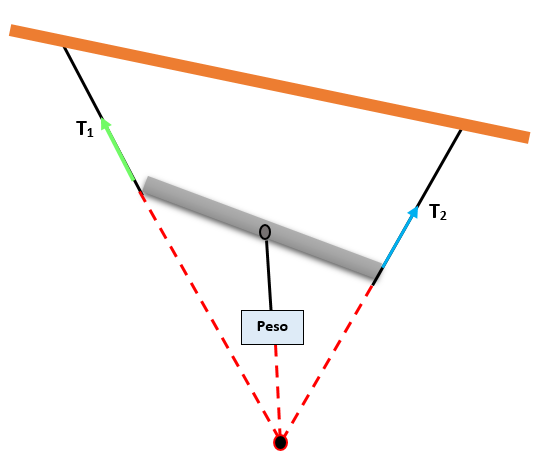
Ainsi, si trois forces qui sont dans le même plan et simultanées, l'ampleur de chaque force sera proportionnelle au sein de l'angle opposé, qui se forment par les deux autres forces.

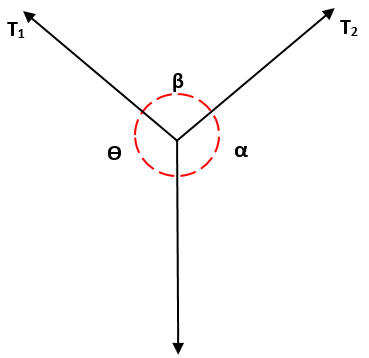
Cela doit T1, à partir du sein de α, il est égal au rapport de T2 / β, qui à son tour est égal au rapport de T3 / ɵ, c'est-à-dire:

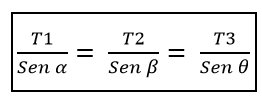
De là, il s'ensuit que les modules de ces trois forces doivent être les mêmes si les angles qui forment chaque paire de forces sont égaux à 120º.

Il est possible que l'un des angles soit obtus (mesure entre 90⁰ et 180⁰). Dans ce cas, le sein de cet angle sera égal au sein de l'angle supplémentaire (dans sa paire, il mesure 180⁰).

Exercice résolu

Il y a un système formé par deux blocs J et K, qui s'accrochent à plusieurs chaînes formant des angles par rapport à l'horizontal, comme indiqué sur la figure. Le système est en équilibre et le bloc J pèse 240 N. Déterminez le poids du bloc K.

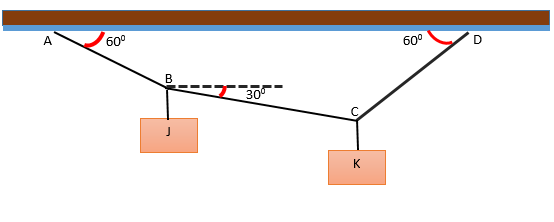
Solution

Par le principe d'action et de réaction, les tensions exercées dans les blocs 1 et 2 seront égales au poids de celles-ci.

Maintenant, un diagramme corporel libre est construit pour chaque bloc et déterminer ainsi les angles qui forment le système.

On sait que la corde qui va à A à B, a un angle de 30⁰ , de sorte que l'angle qui le complète est égal à 60⁰ . De cette façon, vous atteignez 90⁰.

D'un autre côté, où se trouve le point A, il y a un angle de 60⁰ en ce qui concerne l'horizontal; L'angle entre vertical et t_POUR Ce sera = 180⁰ - 60⁰ - 90⁰ = 30⁰.

Ainsi, il est obtenu que l'angle entre AB et BC = (30⁰ + 90⁰ + 30⁰) et (60⁰ + 90⁰ + 60) = 150⁰ et 210⁰. Lors de la rejoindre, il est vérifié que l'angle total est 360⁰.

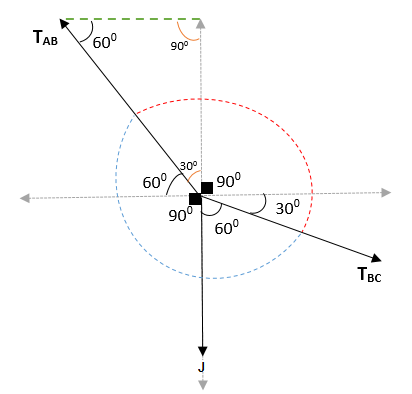
Appliquer le théorème de Lamy, vous devez:

T_{avant JC}/ Sin 150⁰ = P_POUR/ Sin 150⁰

T_{avant JC} = P_POUR

T_{avant JC} = 240N.

Au point C, où est le bloc, l'angle entre l'horizontal et la corde BC est de 30 est 30⁰, Donc l'angle complémentaire est égal à 60⁰.

D'un autre côté, il y a un angle de 60⁰ au point CD; L'angle entre vertical et t_C Ce sera = 180⁰ - 90⁰ - 60⁰ = 30⁰.

Ainsi, il est obtenu que l'angle du bloc K est = (30⁰ + 60⁰)

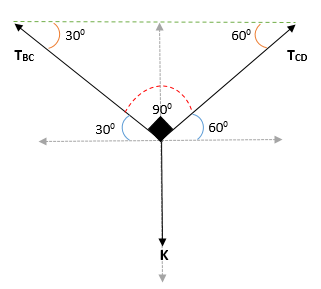
Appliquer le théorème de Lamy au point C:

T_{avant JC}/ Sin 150⁰ = B / sin 90⁰

Q = T_{AVANT JC *} Sen 90⁰ / Sin 150⁰

Q = 240 n * 1 / 0,5

Q = 480 N.

Les références

1. Ferdinand P. Bière, e. R. (2013). Mécanique pour les ingénieurs, statique. McGraw-Hill Inter-American.
2. Francisco Español, J. C. (2015). Problèmes d'algèbre linéaire résolus. Éditions paraninfo, s.POUR.
3. Graham, J. (2005). Force et mouvement. Houchton Mifflin Harcourt.
4. Harpe, p. d. (2000). Sujets de la théorie des groupes géométriques. University of Chicago Press.
5. P. Un tpler y, g. M. (2005). Physique pour la science et la technologie. Volume I. Barcelone: ​​Retournez-vous.POUR.