Théorème d'Euclide

Quel est le théorème d'Euclid?

Il Théorème d'Euclide Il démontre les propriétés d'un triangle droit en dessinant une ligne qui la divise en deux nouveaux rectangles qui sont similaires les uns aux autres et, à leur tour, sont similaires au triangle d'origine; Donc, il y a une relation de proportionnalité.

Euclides était l'un des plus grands mathématiciens et géomètres de la vieillesse qui ont fait plusieurs manifestations de théorèmes importants. L'un des principaux est celui qui porte son nom, qui a eu une large application.

Cela a été le cas parce que, à travers ce théorème, les relations géométriques existant dans le triangle du rectangle explique où cela est lié à leurs projections dans l'hypoténuse.

Formules et démonstration

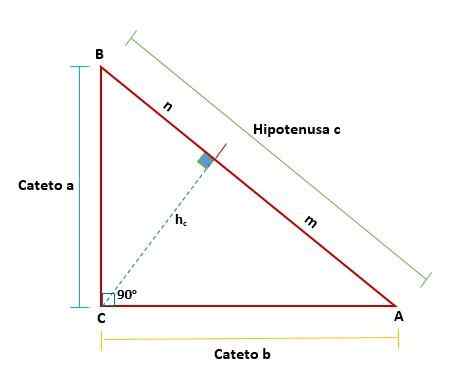
Le théorème d'Euclide propose que dans chaque triangle droit, lorsqu'une ligne est tracée - qui représente à la hauteur qui correspond au sommet de l'angle droit par rapport à l'hypoténuse - deux rectangles sont formés à partir des triangles d'origine de l'original.

Ces triangles seront similaires les uns aux autres et seront également similaires au triangle d'origine, ce qui signifie que leurs côtés similaires sont proportionnels les uns aux autres:

Les angles des trois triangles sont congruents; C'est-à-dire lorsqu'il est tourné à 180 degrés sur son sommet, un angle coïncide sur l'autre. Cela implique que tout le monde sera égal.

De cette façon, vous pouvez également vérifier la similitude qui existe entre les trois triangles, pour l'égalité de ses angles. Depuis la similitude des triangles, Euclide en établit les proportions de deux théorèmes:

• Théorème de hauteur.
• Le théorème des catetos.

Ce théorème a une large application. Dans les temps anciens, il a été utilisé pour calculer les sommets ou les distances, représentant une grande avancée pour la trigonométrie.

Peut vous servir: calcul des approches à l'aide de différentiels

Il est actuellement appliqué dans divers domaines basés sur les mathématiques, comme l'ingénierie, la physique, la chimie et l'astronomie, entre autres domaines.

Théorème de hauteur

Ce théorème établit que dans tout triangle rectangulaire, la hauteur tirée de l'angle droit par rapport à l'hypoténuse est la moyenne proportionnelle géométrique (le carré de la hauteur) entre les projections des cotetos qui déterminent l'hypoténuse.

C'est-à-dire que le carré de la hauteur sera égal à la multiplication des jambes projetées qui forment l'hypoténuse:

H_c² = m _* n

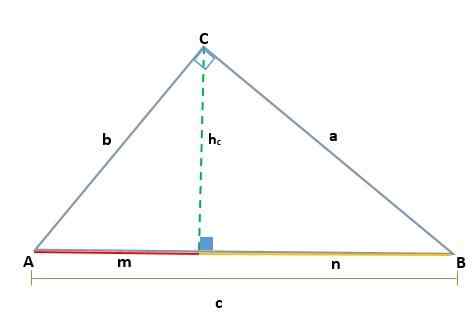
Manifestation

Étant donné un triangle ABC, qui est rectangle dans le sommet C, deux rectangles similaires, ADC et BCD sont générés; Par conséquent, leurs côtés correspondants sont proportionnels:

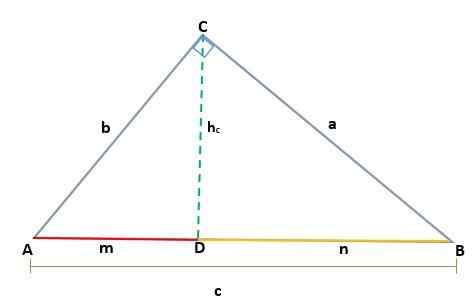
De telle manière que la hauteur h_c Il correspond au segment CD, correspond à l'hypoténuse ab = c, vous devez donc:

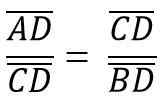
À son tour, cela correspond à:

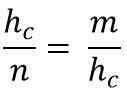
Effacer l'hypoténuse (h_c), Pour multiplier les deux membres de l'égalité, vous devez:

H_{C *} H_{C =} m _* n

H_c² = m _* n

Ainsi, la valeur de l'hypoténuse est donnée par:

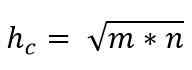
Le théorème des catetos

Ce théorème établit que, dans chaque triangle droit, la mesure de chaque cateto sera la moyenne proportionnelle géométrique (le carré de chaque cateto) entre la mesure de l'hypoténuse (complète) et la projection de chacun à ce sujet:

b² = C _* m

pour² = C_* n

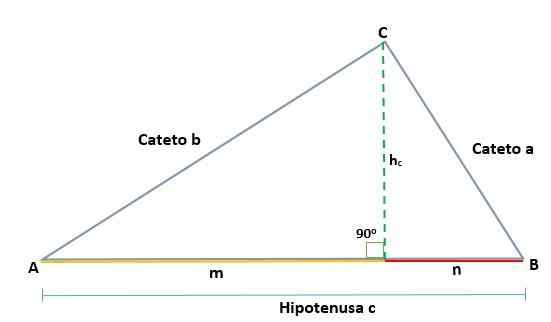
Manifestation

Compte tenu d'un triangle ABC, qui est rectangle dans le sommet C, de sorte que son hypotenusa est c, lors du dessin de la hauteur (h) les projections des catégories A et B sont déterminées, qui sont les segments M et N respectivement, et qui sont sur L'hypoténuse.

Ainsi, la hauteur dessinée sur le triangle rectangle ABC génère deux rectangles similaires, ADC et BCD, de sorte que les côtés correspondants sont proportionnels, comme ceci:

Peut vous servir: paraboloïde hyperbolique: définition, propriétés et exemples

Db = n, qui est la projection du CB Cateto sur l'hypoténuse.

Ad = m, qui est la projection de l'AC Cateto sur l'hypoténuse.

Ensuite, l'hypoténuse C est déterminée par la somme des jambes de ses projections:

C = m + n

En raison de la similitude des triangles ADC et BCD, vous devez:

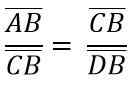
Ce qui précède est le même que:

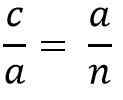
Effacer le "A" Cateto pour multiplier les deux membres de l'égalité, vous devez:

pour _* a = c _* n

pour² = C _* n

Ainsi, la valeur du Cateto «A» est donnée par:

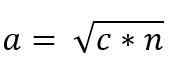
De même, en raison de la similitude des triangles ACB et ADC, vous devez:

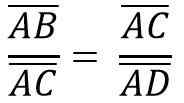
Ce qui précède est égal à:

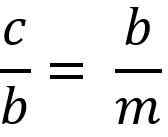
Effacer le Cateto "B" pour multiplier les deux membres de l'égalité, vous devez:

b _* b = c _* m

b² = C _* m

Ainsi, la valeur du Cateto «B» est donnée par:

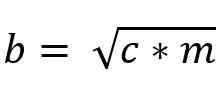
Relation entre les théorèmes euclides

Les théorèmes en référence à la hauteur et les catégories sont liés les uns aux autres car la mesure des deux est faite par rapport à l'hypoténuse du triangle rectangle.

Grâce à la relation des théorèmes euclides, la valeur de la hauteur peut également être trouvée; Cela est possible en effacant les valeurs de m et n du théorème de catégorie et sont remplacées dans le théorème de hauteur. De cette façon, il est accompli que la hauteur est égale à la multiplication des jambes, divisée par l'hypoténuse:

b² = C _* m

M = B² ÷ c

pour² = C _* n

n = a² ÷ c

En hauteur, le théorème M et N est remplacé:

H_c² = m _* n

H_c² = (b² ÷ c) _* (pour² ÷ c)

H_c = (b² _* pour²) ÷ c

Exercices résolus

Exemple 1

Compte tenu du triangle ABC, rectangle dans A, déterminez la mesure de la CA et de la MA, si AB = 30 cm et BD = 18 cm

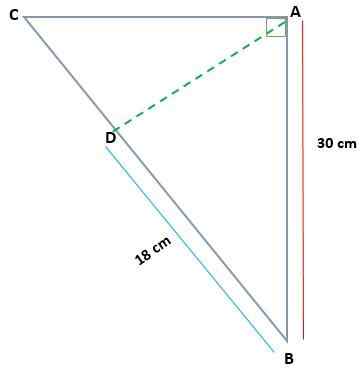
Solution

Dans ce cas, il existe les mesures de l'une des jambes projetées (BD) et de l'une des tarks du triangle d'origine (AB). De cette façon, vous pouvez appliquer le théorème de la catégorie pour trouver la valeur de la BC Cateto.

Peut vous servir: règle de correspondance d'une fonction

UN B² = BD _* avant JC

(30)² = 18 _* avant JC

900 = 18 _* avant JC

BC = 900 ÷ 18

BC = 50 cm

La valeur du CD Cateto peut être trouvée sachant que BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Maintenant, il est possible de déterminer la valeur de l'AC Cateto, en appliquant à nouveau le théorème de la catégorie:

CA² = CD _* Bd

CA² = 32 _* cinquante

CA² = 160

AC = √1600 = 40 cm

Pour déterminer la valeur de hauteur (AD), le théorème de hauteur s'applique, car les valeurs des catégories projetées CD et BD sont connues:

PUBLICITɲ = 32 _* 18

PUBLICITɲ = 576

AD = √576

AD = 24 cm

Exemple 2

Déterminez la valeur de la hauteur (h) d'un triangle MNL, rectangle en n, connaissant les mesures des segments:

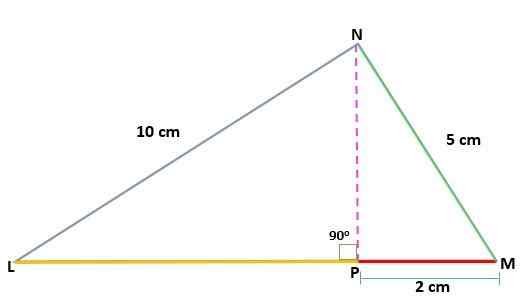
Nl = 10 cm

Mn = 5 cm

PM = 2 cm

Solution

Vous avez la mesure de l'une des jambes projetées sur l'hypoténuse (PM), ainsi que les mesures des catégories de triangle d'origine. De cette façon, vous pouvez appliquer le théorème de la catégorie pour trouver la valeur de l'autre Cateto projeté (LN):

Nl² = Pm _* LM

(dix)² = 5 _* LM

100 = 5 _* LM

PL = 100 ÷ 5 = 20

Comme la valeur des catégories et de l'hypoténuse est déjà connue, à travers la relation des théorèmes de hauteur et les catégories peuvent être déterminées la valeur de la hauteur:

Nl = 10

Mn = 5

Lm = 20

H = (b² _* pour²) ÷ c.

H = (10² _* 5²)  ÷ (vingt)

H = (100 _* 25) ÷ (vingt)

H = 2500 ÷ vingt

H = 125 cm.