Théorème de Bolzano

Nous expliquons ce qu'est le théorème de Bolzano, ses applications et ont mis des exercices résolus

Quel est le théorème de Bolzano?

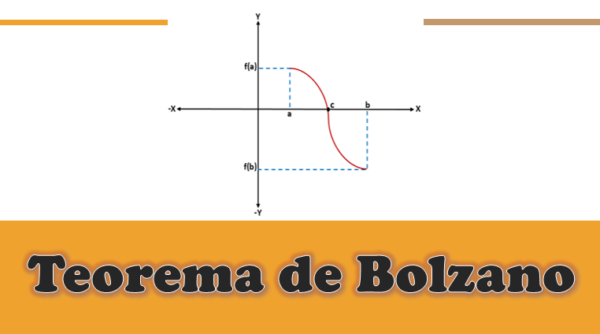
Il Théorème de Bolzano Il établit que si une fonction est continue à tous les points d'un intervalle fermé [a, b] et qu'il est rempli que l'image de «A» et «B» (sous la fonction) ait des signes opposés, alors il y aura au moins un point "C" dans l'intervalle ouvert (a, b), de sorte que la fonction évaluée en "C" sera égale à 0.

Ce théorème a été déclaré par le philosophe, le théologien et le mathématicien Bernard Bolzano en 1850. Ce scientifique, né en République tchèque actuelle, a été l'une des premières mathématiques de l'histoire à faire une démonstration formelle des propriétés des fonctions continues.

Explication du théorème

Le théorème de Bolzano est également connu comme le théorème des valeurs intermédiaires, ce qui aide à déterminer les valeurs spécifiques, en particulier les zéros, de certaines fonctions réelles d'une variable réelle.

Dans une fonction donnée, F (x) continue - c'est-à-dire que F (a) et F (b) sont connectés par une courbe, où f (a) est en dessous de l'axe x (est négatif) et f (b) par au-dessus de l'axe x (il est positif), ou vice versa, il y aura un point de coupe sur l'axe x qui représentera une valeur intermédiaire "C", qui sera entre "A" et "B", et la valeur de f (c) il sera égal à 0.

Lors de l'analyse graphiquement du théorème de Bolzano, on peut savoir que pour toute fonction F continue définie dans un intervalle [a, b], où f (a)_*f (b) est inférieur à 0, il y aura au moins une racine «C» de cette fonction dans l'intervalle (a, b).

Ce théorème n'établit pas le nombre de points existant dans cet intervalle ouvert, il indique seulement qu'il y a au moins 1 point.

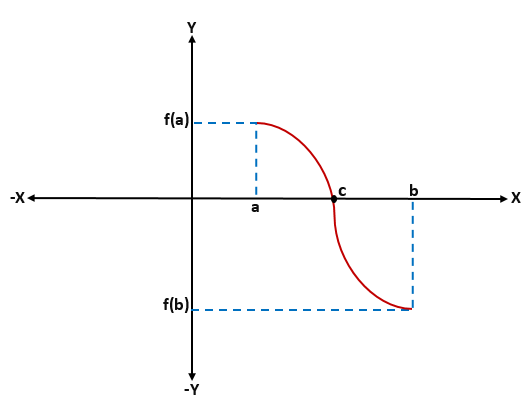
Démonstration du théorème de Bolzano

Pour démontrer le théorème de Bolzano, il est supposé sans perte de généralité que f (a) 0; De cette façon, il peut y avoir de nombreuses valeurs entre "a" et "b" pour lequel f (x) = 0, mais il est seulement nécessaire de démontrer qu'il y en a un.

Peut vous servir: Nombres imaginaires: propriétés, applications, exemples

Il commence à évaluer f au milieu (a + b) / 2. Si f ((a + b) / 2) = 0 alors le test se termine ici; Sinon, alors f ((a + b) / 2) est positif ou négatif.

L'une des moitiés de l'intervalle [a, b] est choisie, de sorte que les signes de la fonction évalués aux extrémités sont différents. Ce nouvel intervalle sera [A1, B1].

Maintenant, si F évalué au milieu de [A1, B1] n'est pas nul, la même opération est effectuée avant; C'est-à-dire que la moitié de cet intervalle qui répond à l'état des signes est choisi. Être ce nouvel intervalle [A2, B2].

Si ce processus continue, il y aura deux successions an et bn, telles que:

an se développe et bn diminue:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Si la longueur de chaque intervalle [ai, bi] est calculée, vous devrez:

B1-A1 = (B-A) / 2.

B2-A2 = (B-A) / 2².

.. .

bn-an = (b-a) / 2 ^ n.

Par conséquent, la limite lorsque n tend à l'infini de (bn-an) est égal à 0.

En utilisant que an est en croissance et limité et bn est en baisse et limité, il y a une valeur "C" telle que:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

La limite LIM est "C" et la limite de bn est également "C". Par conséquent, étant donné tout Δ> 0, il y a toujours un «n» tel que l'intervalle [an, bn] est contenu dans l'intervalle (c-δ, c + Δ).

Maintenant, il faut montrer que f (c) = 0.

Si f (c)> 0, alors comme f est continu, il y a un ε> 0 tel que f est positif tout au long de l'intervalle (C -ε, C + ε). Cependant, comme indiqué ci-dessus, il y a une valeur «n» telle que F modifie la connexion [an, bn] et, en outre, [an, bn] est contenue à l'intérieur (C -ε, C + ε), ce qui est une contradiction.

Si f (c) 0 tel que f est négatif tout au long de l'intervalle (c -ε, c + ε); Mais il y a une valeur «n» que F change de connexion [an, bn]. Il s'avère que [an, bn] est contenu à l'intérieur (c -ε, c + ε), qui est également une contradiction.

Peut vous servir: signes de regroupement

Par conséquent, f (c) = 0 et c'est ce qui voulait être démontré.

Quel est le théorème de Bolzano pour?

À partir de son interprétation graphique, le théorème de Bolzano est utilisé pour trouver des racines ou des zéros dans une fonction continue, par bission (approche), qui est une méthode de recherche incrémentielle qui divise toujours les intervalles en 2.

Ainsi, si la fonction change de signe sur un intervalle, la fonction F est évaluée au milieu, qui est exprimée comme suit: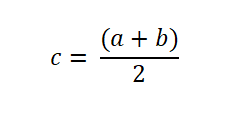La racine est trouvée lorsque f (c) = 0. Sinon, le signe de f (c) est analysé pour déterminer s'il est opposé au signe de f (a) ou celui de f (b).

Alors un intervalle [a, c] ou [c, b] est pris lorsque le changement de signe se produit, et le processus est répété jusqu'à ce que l'intervalle soit de moindre et moindre, afin d'approcher la valeur que vous souhaitez; c'est-à-dire à la valeur que fait la fonction 0.

En résumé, pour appliquer le théorème de Bolzano et donc trouver les racines, limiter les zéros d'une fonction ou donner une solution à une équation, les étapes suivantes sont effectuées:

1. Il est vérifié si F est une fonction continue dans l'intervalle [a, b].
2. Si l'intervalle n'est pas donné, il faut en trouver un où la fonction est continue.
3. Il est vérifié si les extrémités de l'intervalle donnent des signes opposés lorsqu'ils sont évalués en f.
4. Si les signes opposés ne sont pas obtenus, l'intervalle doit être divisé en deux sous-intervalles en utilisant le point médian.
5. Évaluez la fonction au milieu et vérifiez que l'hypothèse de Bolzano est remplie, où f (a) _* f (b) < 0.
6. Selon le signe (positif ou négatif) de la valeur trouvée, le processus est répété avec un nouveau sous-intervalle jusqu'à ce que l'hypothèse mentionnée soit respectée.

Peut vous servir: Programmation non linéaire: méthodes et exercices

Exercices résolus

Exercice 1

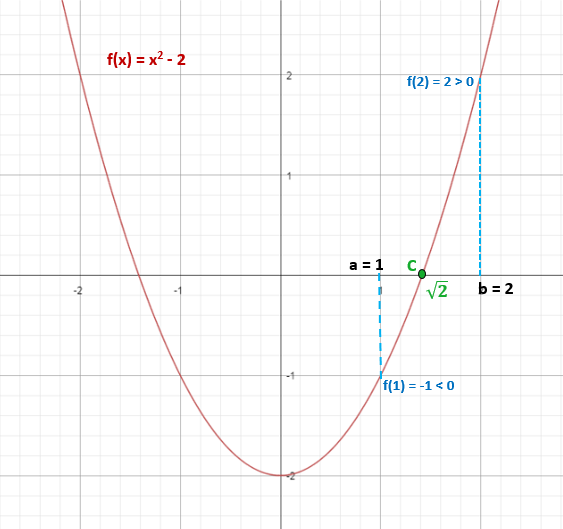
Déterminez si la fonction f (x) = x² - 2, a au moins une vraie solution dans l'intervalle [1,2].

Solution

Vous avez la fonction f (x) = x² - 2. Comme c'est le polynôme, cela signifie qu'il est continu dans n'importe quel intervalle.

Il est demandé de déterminer s'il a une véritable solution dans l'intervalle [1, 2], donc maintenant vous n'avez qu'à remplacer les extrémités de l'intervalle dans la fonction pour connaître le signe de ceux-ci et savoir s'ils répondent à l'état d'être différent:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (négatif)

f (2) = 2² - 2 = 2 (positif)

Par conséquent, signe de f (1) ≠ signe f (2).

Cela garantit qu'il y a au moins un point «C» qui appartient à l'intervalle [1,2], dans lequel f (c) = 0.

Dans ce cas, la valeur «C» peut être calculée facilement comme suit:

X² - 2 = 0

x = ± √2.

Ainsi, √2 ≈ 1,4 appartient à l'intervalle [1,2] et remplit ce f (√2) = 0.

Exercice 2

Démontrer que l'équation x⁵ + x + 1 = 0 a au moins une vraie solution.

Solution

Nous notons d'abord que f (x) = x⁵ + X + 1 est une fonction polynomiale, ce qui signifie qu'il est continu dans tous les nombres réels.

Dans ce cas, aucun intervalle n'est donné, vous devez donc choisir des valeurs intuitivement, de préférence près de 0, pour évaluer la fonction et trouver les changements de signe:

Si l'intervalle [0, 1] est utilisé, il doit:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Comme il n'y a pas de changement de signe, le processus est répété avec un autre intervalle.

Si l'intervalle [-1, 0] est utilisé, vous devez:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

Dans cet intervalle, il y a un changement de signe: signe de f (-1) ≠ signe de f (0), ce qui signifie que la fonction f (x) = x⁵ + X + 1 a au moins une véritable racine «C» dans l'intervalle [-1, 0], tel que f (c) = 0. En d'autres termes, il est vrai que x⁵ + x + 1 = 0 a une véritable solution dans l'intervalle [-1,0].