Théorème de Bernoulli

Nous expliquons ce qu'est le théorème, les équations, les applications de Bernoulli et résoudre un exercice

Quel est le théorème de Bernoulli?

Il Théorème de Bernoulli Il affirme que, dans un fluide idéal circulant dans un conduit, l'énergie mécanique par unité de volume du fluide est constante dans toutes les sections du tube, quelle que soit leur section transversale différente de l'aire et de la hauteur.

Maintenant, un fluide idéal est celui qui ne peut pas être comprimé, donc sa densité est fixe, quelle que soit la valeur de pression.

De plus, un fluide idéal n'a aucune viscosité, c'est-à-dire qu'il n'y a pas de friction entre les couches de fluide et ni entre le fluide et les murs du conduit.

Les conditions d'incompressibilité et de viscosité nul sont essentielles pour appliquer le théorème de Bernoulli. Il est également nécessaire que le flux soit stationnaire, c'est-à-dire que le flux ne varie pas dans le temps.

D'un autre côté, le flux doit être laminaire, donc il ne peut y avoir de tourbillon ni de turbulence pendant le passage du conduit.

Équation de Bernoulli

L'équation de Bernoulli a trois termes, le travail effectué par la presse P, l'énergie cinétique et l'énergie du potentiel gravitationnel pour chaque unité de fluide de densité volumétrique ρ

L'équation de Bernoulli est:

D'un autre côté, l'équation de continuité établit que dans un fluide idéal, l'écoulement est constant dans toutes les sections du tube d'écoulement. C'est-à-dire que le volume de liquide dans la même unité de temps est le même dans toutes les sections du tube.

Si le flux est Q, alors:

Q = constant

Avec:

Q = A · V

Où a est la zone transversale du tube et V est la vitesse du fluide.

Peut vous servir: satellites artificiels

Il est à noter que dans les sections les plus étroites du tube, le fluide doit circuler plus rapidement, car il reste constant bien qu'il varie. Par conséquent, l'énergie cinétique par unité de volume est plus élevée.

Puisque le théorème de Bernoulli établit que l'énergie mécanique est constante dans toutes les sections, dans les sections plus étroites d'une plus grande énergie cinétique, l'énergie potentielle diminue. 

L'énergie potentielle se compose d'énergie gravitationnelle par volume unitaire plus le travail effectué par la pression dans un volume unitaire, par conséquent, en diminuant l'énergie potentielle diminue également la pression.

En résumé, l'effet combiné du principe de continuité et du théorème de Bernoulli entraîne des sections étroites du tube d'écoulement, où la vitesse du fluide est plus élevée, la pression tombe par rapport aux sections plus larges.

Termes dans l'équation de Bernoulli

1) Travail effectué par la pression par unité de volume 

Dans une section de section transversale de la zone à, Le fluide fait un montant s, En raison de la pression p qui produit une force f = p⋅ a.

Le travail effectué par la force est:

F⋅ s = p⋅ a⋅ s

Comme le produit A⋅s représente le volume déplacé, le travail effectué par unité de volume correspond numériquement à la valeur de P dans la section considérée.

2) Énergie cinétique d'un volume unitaire de liquide

Comme le fluide est incompressible, sa densité a une valeur fixe appelée ρ.

Lorsque le fluide circule à travers une section de la section transversale A, déplaçant une quantité s dans un temps t, le débit est:

Il peut vous servir: deuxième loi de la thermodynamique: formules, équations, exemples

v = s / t

Et l'énergie cinétique de ladite partie fluide est calculée par:

K = ½ ρ (a⋅s) v²

Mais si le volume déplacé (a⋅s) est unit, alors le terme d'énergie cinétique sera donné de ½ ρ V².

3) Énergie potentielle gravitationnelle d'un volume unitaire de liquide à une hauteur h 

Pour une partie liquide de pâte m et la hauteur H En ce qui concerne un certain niveau de référence, l'énergie gravitationnelle est donnée par:

U = m⋅ g⋅ h

Si la pâte m Il correspond à une partie fluide unitaire, puis la masse de la partie correspond à la densité ρ, Donc l'énergie potentielle sera ρ⋅ g⋅ h.

Applications du théorème de Bernoulli

Soutien aérodynamique

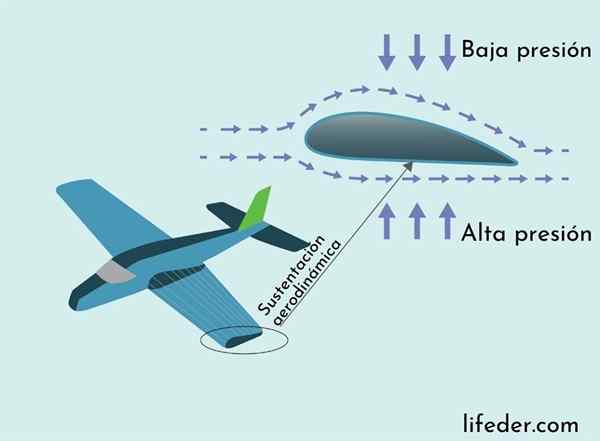Le soutien aérodynamique s'explique par le théorème de Bernoulli

La force qui empêche un avion de s'effondrer est la force de soutien aérodynamique. La force de support nette est dirigée verticalement et agit le long de l'aile plane. Son origine est expliquée à travers le théorème de Bernoulli.

L'aile d'un avion a une section transversale avec une courbe plus longue en haut et plus court en bas. Cela rend la route d'air près de la surface de l'aile en haut, de sorte que l'air s'écoule plus rapidement au-dessus de l'aile que le fond. 

En conséquence du théorème de Bernoulli, la pression de l'air dans la partie supérieure de l'aile circulante est inférieure qu'au fond, ce qui entraîne la force exercée par la différence de pression vers le haut, soutenant le poids du plan, selon lui vu dans l'image suivante.

Il peut vous servir: physique pendant les Grecs (Grec antigèse)

Lancement de balles et de balles avec effet courbe

Dans certains sports tels que le football, le baseball et le Cricke, les joueurs expérimentés savent comment. Est ce qu'on appelle Lancement d'effet.

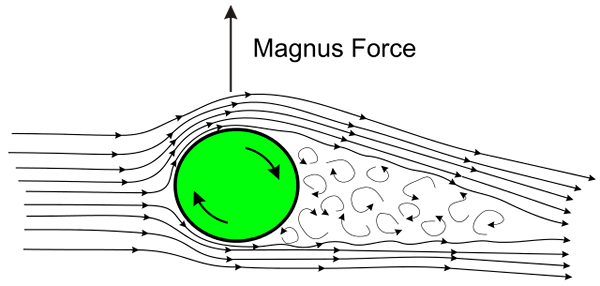Illustration de l'effet Magnus. Source: Wikimedia Commons

L'effet se produit chaque fois que la balle ou la balle tourne rapidement tout en se déplaçant dans l'air. La rotation fait que l'air à la surface de la balle est traînée par lui dans deux directions opposées, une en faveur de la direction de la traduction et, de l'autre côté, dans la direction de déplacement.

À la suite de la traînée d'air, une zone de basse pression est produite sur une face de la balle et sur la face opposée une haute pression, produisant une force nette qui détourne la trajectoire naturelle de la balle.

L'explication de ce phénomène connu sous le nom Effet Magnus Il réside précisément dans le théorème de Bernoulli: où le fluide circule rapidement, la pression est faible, et sur le côté où la pression circule lentement.

Exercice résolu

Un tube horizontal a une section de zone A₁ = 40 centimètres carrés et une autre section de la section de la zone A₂ quatre fois plus bas. Si le débit d'eau est de 6 L / s, déterminez la différence de pression et la différence de hauteur dans les tubes verticaux.

Solution 

À partir de l'équation de flux, dont la valeur est q = 6 l / s:

Q = A · V

Vous devez alors la vitesse dans la section large est de 1,5 m / s et dans l'étirement étroit de 6 m / s.

Ensuite, en appliquant et en correspondant à l'équation de Bernoulli sur l'étirement large et étroit, une différence de pression de 1700 PA est obtenue, ce qui correspond à une différence de hauteur dans les tubes verticaux de 1,72 mètre.