Théorie des caractéristiques des ensembles, éléments, exemples, exercices

La théorie de la théorie C'est une branche de la logique-mathématique qui est responsable de l'étude des relations entre les entités appelées ensembles. Les ensembles sont caractérisés par des collections d'objets de même nature. Ces objets sont les éléments de l'ensemble et peuvent être: nombres, lettres, figures géométriques, mots qui représentent des objets, les objets eux-mêmes et les autres.

C'était Georg Cantor, vers la fin du 19e siècle, qui a proposé l'ensemble des ensembles. Alors que d'autres mathématiciens notables au XXe siècle ont fait leur formalisation: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel, entre autres.

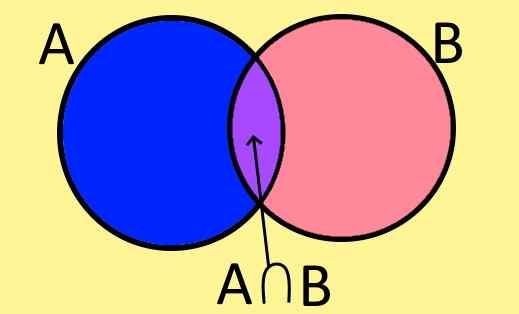
Figure 1. Diagramme de Venn des ensembles A, B et leur intersection A⋂ B. (Élaboration propre).

Les diagrammes de Venn sont le moyen graphique de représenter un ensemble et se compose d'une figure plate fermée dans laquelle les éléments de l'ensemble sont.

Par exemple, la figure 1 montre deux ensembles A et B, qui ont des éléments en commun, les éléments communs à A et B. Ceux-ci forment un nouvel ensemble appelé l'ensemble d'intersection de A et B, qui est écrit symboliquement comme suit:

A ∩ B

[TOC]

Caractéristiques

L'ensemble est un concept primitif tel qu'il est en géométrie le concept de point, droit ou plat. Il n'y a pas de meilleur moyen d'exprimer le concept que de souligner des exemples: 

L'ensemble et formé par les couleurs du drapeau de l'Espagne. Cette façon d'exprimer l'ensemble est appelée par la compréhension. Le même ensemble et écrit par extension est:

E = rouge, jaune

Dans ce cas, le rouge et le jaune sont des éléments de l'ensemble et. Il convient de noter que les éléments sont répertoriés entre les clés et ne sont pas répétés. Dans le cas du drapeau espagnol, il y a trois rayures de couleurs (rouge, jaune, rouge) dont deux sont répétées, mais les éléments ne sont pas répétés lorsque l'ensemble est exprimé.

Supposons que Set V soit formé par les trois premières lettres vocales:

V = a, e, i

La puissance de V, qui est désignée par P (v) est l'ensemble de tous les ensembles qui peuvent être formés avec les éléments de V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Types d'ensembles

Ensemble fini

C'est un ensemble dans lequel ses éléments sont nuables. Des exemples d'ensembles finis sont les lettres de l'alphabet espagnol, les voyelles d'espagnol, les planètes du système solaire entre autres. Le nombre d'éléments d'un ensemble fini est appelé sa cardinalité.

Ensemble infini

Ensemble infini, tous ceux dont le nombre de ses éléments est inconfortable, car quelle que soit la taille du nombre de ses éléments pour trouver plus d'éléments.

Un exemple de jeu infini est l'ensemble des nombres naturels n, qui est largement exprimé comme suit:

Peut vous servir: Coplanares Points: équation, exemple et exercices résolus

N = 1, 2, 3, 4, 5, .. . est clairement un ensemble infini, car peu importe la taille d'un nombre naturel, la majeure suivante peut toujours trouver dans un processus sans fin. De toute évidence, la cardinalité d'un ensemble infini est ∞.

Ensemble vide

C'est l'ensemble qui ne contient aucun élément. L'ensemble vide V est indiqué par Ø ou au moyen d'une paire de clés sans éléments à l'intérieur:

V = = Ø.

L'ensemble vide est unique, il doit donc être incorrect de dire "un ensemble vide", le formulaire correct est de dire "l'ensemble vide".

Parmi les propriétés de l'ensemble vide, c'est qu'il est sous-ensemble de n'importe quel ensemble:

Ø ⊂ A

De plus, si un ensemble est sous-ensemble de l'ensemble vide, cet ensemble sera nécessairement le vide:

A ⊂ Ø ⇔ a = Ø

Ensemble unitaire

Il s'appelle l'ensemble unitaire tout ensemble qui contient un seul élément. Par exemple, l'ensemble des satellites naturels de la Terre est un ensemble d'unités, dont le seul élément est la lune. L'ensemble B de nombres entiers inférieurs à 2 et supérieurs à zéro n'a que l'élément 1 donc c'est un ensemble d'unités.

Ensemble binaire

Un ensemble est binaire s'il n'a que deux éléments. Par exemple définir x, tel que x est un réel nombre de x ^ 2 = 2 = 2. Cet ensemble par extension est écrit comme ceci:

X = --√2, + √2

Ensemble universel

L'ensemble universel est un ensemble qui contient d'autres ensembles du même type ou de la même nature. Par exemple, l'ensemble universel de nombres naturels est l'ensemble des nombres réels. Mais les nombres réels sont également universels des nombres entiers et des nombres rationnels.

Éléments essentiels

- Relations entre les ensembles

Dans les ensembles, vous pouvez établir plusieurs types de relations entre eux et leurs éléments. Si deux ensembles A et B ont exactement les mêmes éléments, parmi eux, une relation égale est indiquée comme suit:

POUR = B

Si tous les éléments d'un ensemble pour appartenir à un ensemble B, mais que tous les éléments de B appartiennent à A, alors parmi ces ensembles, il y a une relation d'inclusion qui est indiquée comme suit:

A ⊂ b, mais b ⊄ a

L'expression précédente se lit.

Pour indiquer que certains éléments ou certains éléments appartiennent à un ensemble est utilisé le symbole d'appartenance ∈, par exemple pour dire que l'élément ou les éléments appartiennent à l'ensemble A est écrit symboliquement comme suit:

x ∈ A

Oui, un élément et n'appartient pas à l'ensemble de cette relation est écrit comme ceci:

et ∉ A

La relation d'appartenance est donnée entre les éléments d'un ensemble et l'ensemble, à la seule exception de l'ensemble de puissance, l'ensemble étant la collection ou l'ensemble de tous les ensembles possibles qui peuvent être formés avec les éléments dudit ensemble.

Peut vous servir: factorisation

Supposons v = a, e, i, votre pouvoir est p (v) = a, e, i, a, e, a, i, e, i, a, e, i, dans ce cas, l'ensemble v devient un élément de l'ensemble p (v) et peut être écrit:

V ∈ P (v)

- Propriétés d'inclusion

La première propriété d'inclusion établit que chaque ensemble est contenu en soi, ou en d'autres termes, qui est sous-ensemble de lui-même:

A ⊂ A

L'autre propriété de l'inclusion est la transitivité: si A est un sous-ensemble de B et B à son tour, il est sous-ensemble de C, alors A est sous-ensemble de C. Symbolly La relation de transitivité est écrite comme ceci:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Vous trouverez ci-dessous le diagramme de Venn correspondant à la transitivité de l'inclusion:

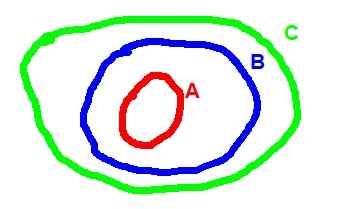Figure 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Opérations entre les ensembles

Intersection

L'intersection est une opération entre deux ensembles qui se traduit par un nouvel ensemble appartenant au même ensemble universel des deux premiers. En ce sens, c'est une opération fermée.

Symboliquement, l'opération d'intersection est formulée comme suit:

A⋂b = x / x∈A ^ x∈B

Un exemple est le suivant: Définissez A des lettres du mot "éléments" et définissez B des lettres du mot "répété", l'intersection entre A et B est écrite comme celle-ci:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . L'ensemble universel de A, de B et aussi de A⋂b est l'ensemble des lettres de l'alphabet espagnol.

syndicat

L'union de deux ensembles est l'ensemble formé par les éléments communs aux deux ensembles et les éléments non communs des deux ensembles. L'opération syndicale entre les ensembles est exprimée symboliquement comme suit:

A∪b = x / x∈A v x∈B

Différence

Le fonctionnement de l'ensemble au moins l'ensemble est indiqué par A-B. A-B est un nouvel ensemble formé par tous les éléments qui sont dans A et qui n'appartiennent pas à B. Le symbole est écrit comme ceci:

A - b = x / x ∈ A ^ x ∉ b

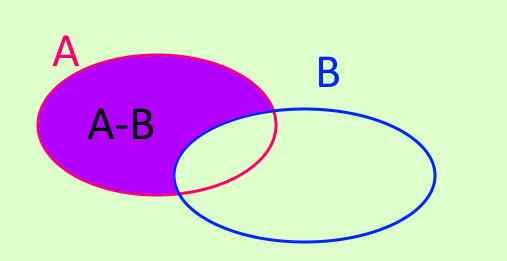figure 3. A - b = x / x ∈ A ^ x ∉ b

Différence symétrique

La différence symétrique est une opération entre deux ensembles où l'ensemble résultant est composé des éléments non communs aux deux ensembles. La différence symétrique symboliquement est représentée comme suit:

A⊕b = x / x∈ (a-b) ^ x∈ (b-a)

Exemples

Exemple 1

Le diagramme de Venn est un moyen graphique de représenter les ensembles. Par exemple, l'ensemble C des lettres de l'ensemble de mots est représenté comme suit:

Exemple 2

Il est illustré ci-dessous à travers des diagrammes de Venn que, l'ensemble des voyelles dans le mot "set", est un sous-ensemble de l'ensemble des lettres du mot "ensemble".

Peut vous servir: échantillonnage de quota: méthode, avantages, inconvénients, exemples

Exemple 3

Ensemble Ñ D'après les lettres de l'alphabet espagnol, c'est un ensemble fini, cet ensemble par extension est écrit comme ceci:

Ñ = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z et its La cardinalité est 27.

Exemple 4

Ensemble V Depuis les voyelles en espagnol, c'est un sous-ensemble de l'ensemble ñ:

V ⊂ Ñ C'est donc un ensemble fini.

L'ensemble fini V La manière étendue, il est écrit comme ceci: V = a, e, i, o, u et sa cardinalité est 5.

Exemple 5

Étant donné les ensembles a = 2, 4, 6, 8 et b = 1, 2, 4, 7, 9 déterminez A-B et B-A. 

A - b sont les éléments dont ils ne sont pas en b:

A - b = 6, 8

B - A sont les éléments de B qui ne sont pas en A:

B - a = 1, 7, 9

Exercices résolus

Exercice 1

Écrivez symbolique et aussi par extension le pétale P des nombres naturels encore inférieurs à 10.

Solution: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Exercice 2

Supposons le tout à celui formé par les nombres naturels qui sont des facteurs de 210, et l'ensemble B qui s'est formé par les nombres naturels inférieurs à 9. Déterminez les deux ensembles par extension et établissez quelle relation il y a entre les deux ensembles.

Solution: Pour déterminer les éléments de l'ensemble A, vous devez commencer par trouver les facteurs du numéro naturel 210:

210 = 2 * 3 * 5 * 7

Puis set a est écrit:

A = 2, 3, 5, 7

Nous continuons à considérer l'ensemble B, qui est les cousins ​​plus petits que 9. Le 1 n'est pas cousin car il ne répond pas à la définition du cousin: "Un nombre est cousin si et seulement s'il a exactement deux diviseurs le 1 et le nombre lui-même". Le 2 est uniforme et en même temps est le cousin car il répond à la définition du cousin, les autres cousins ​​plus petits que 9 sont 3, 5 et 7. De sorte que l'ensemble B est:

B = 2, 3, 5, 7

Par conséquent, les deux ensembles sont les mêmes: un = B.

Exercice 3

Déterminer l'ensemble dont les éléments x sont différents de x.

Solution: C = x / x ≠ x

Comme tout élément, nombre ou objet est égal à lui-même, le set C ne peut pas être autre que l'ensemble vide:

C = Ø

Exercice 4

Être l'ensemble de n de nombres naturels et z L'ensemble des nombres entiers. Déterminer n ⋂ z y n ∪ z.

Solution: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z parce que n ⊂ z.

Les références

1. Garo, m. (2014). Mathématiques: équations quadratiques: comment résoudre une équation quadratique. Marilù Garo.
2. Haeussler, e. F., & Paul, R. S. (2003). Mathématiques pour l'administration et l'économie. Pearson Education.
3. Jiménez, J., Rodríguez, M., Estrada, R. (2005). Mathématiques 1 sept. Seuil.
4. Précieux, c. T. (2005). Cours de mathématiques 3O. Progreso éditorial.
5. Mathématiques 10 (2018). "Exemples d'ensembles finis". Récupéré de: Mathematics10.filet
6. Wikipédia. Théorie de la théorie. Récupéré de: est.Wikipédia.com