Somme des polynômes, comme cela est fait, des exemples, des exercices

La Somme des polynômes C'est l'opération qui consiste à ajouter deux polynômes ou plus, résultant en un autre polynôme. Pour le réaliser, il est nécessaire d'ajouter les termes du même ordre de chacun des polynômes et d'indiquer la somme résultante.

Nous passons d'abord en revue brièvement la signification des "termes du même ordre". Un polynôme d'un n'importe qui se compose de sommes et / ou de soustraction des termes.

Figure 1. Pour ajouter deux polynômes, il est nécessaire de les commander, puis de réduire les termes similaires. Source: Pixabay + Wikimedia Commons.

Les termes peuvent être des produits de nombres réels et une ou plusieurs variables, représentées par des lettres, par exemple: 3X² et -√5.pour²avant JC³ Ce sont des termes.

Eh bien, les termes du même ordre sont ceux qui ont le même exposant ou la même puissance, bien qu'ils puissent avoir un coefficient différent.

-Les termes d'ordre égal sont: 5x³, √2 x³ et -1 / 2x³

-Différents commandes Termes: -2x^-2, 2xy^-1 et √6x²et

Il est important de garder à l'esprit que seuls les termes du même ordre peuvent être ajoutés ou soustraits, une opération connue sous le nom de réduction. Sinon, la somme est simplement laissée indiquée.

Une fois le concept de termes du même ordre clarifié, les polynômes sont ajoutés à la suite de ces étapes:

-Ordonner D'abord les polynômes à ajouter, le tout de la même manière, augmentant ou diminuant, c'est-à-dire avec les pouvoirs du moins au plus grand ou vice versa.

-Compléter, Dans le cas où toute puissance dans la séquence est manquante.

-Réduire Les termes similaires.

-Indiquer La somme résultante.

[TOC]

Exemples de somme polynomiale

Nous allons commencer par ajouter deux polynômes avec une seule variable appelée X, par exemple les polynômes p (x) et q (x) donnés par:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Suivant les étapes décrites, il commence par les commander de manière décroissante, ce qui est le moyen le plus habituel:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Il peut vous servir: angle inscrit d'un cercle: définition, théorèmes, exemples

Q (x) = x⁵+ X² - 25x

Le polynôme Q (x) n'est pas complet, on voit que les pouvoirs avec l'exposant 4, 3 et 0. Ce dernier est simplement le terme indépendant, celui qui n'a pas de lettre.

Q (x) = x⁵+ 0x⁴ + 0x³ + X² - 25x + 0

Une fois cette étape terminée, ils sont prêts à ajouter. Vous pouvez ajouter les termes similaires, puis indiquer la somme, ou placer les polynômes commandés les uns par les autres et réduire par des colonnes, de cette manière:

- X⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ X⁵ + 0x⁴ + 0x³  +  X²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Il est important de noter que lorsqu'il est ajouté, cela se fait algébriquement en respectant la règle des signes, de cette manière 2x + (-25 x) = -23x. Autrement dit, si les coefficients ont un signe différent sont soustraits et que le résultat porte le signe du major.

Ajouter deux polynômes ou plus avec plus d'une variable

En ce qui concerne les polynômes avec plus d'une variable, l'un d'eux est choisi pour le commander. Par exemple, supposons qu'il est demandé d'ajouter:

R (x, y) = 5x²  - 4Y² +  8xy - 6y³ 

ET:

T (x, y) = ½ x²- 6 ans²  - 11xy + x³et

L'une des variables est choisie, par exemple le X à commander:

R (x, y) = 5x² +  8xy - 6y³  - 4Y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Les conditions manquantes sont immédiatement terminées, selon laquelle chaque polynôme a:

R (x, y) = 0x³et + 5x² +  8xy - 6y³  - 4Y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6 ans² 

Et les deux sont prêts à réduire les termes similaires:

0x³et + 5x² +  8xy - 6y³  - 4Y²

Peut vous servir: coefficient de détermination: formules, calcul, interprétation, exemples

+ X³y + ½ x² - 11xy + 0y³ - 6 ans²       +

-

+ X³Y + 11 / 2x² - 3xy - 6y³  - 10Y²    = R (x, y) + t (x, y)

Exercices de somme polynomiale

- Exercice 1

Dans la somme suivante des polynômes, indiquez le terme qui doit aller dans le blanc pour obtenir la somme polynomiale:

-5x⁴  + 0x³ +  2x²         + 1

X⁵  + 2x⁴             - 21X² + 8x - 3

2x⁵             +9x³             -14X

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Solution

Pour obtenir -6x⁵ Un terme du formulaire de hache est requis⁵, tel que:

A + 1+ 2 = -6

Donc:

A = -6-1-2 = -9

Et le terme recherché est:

-9x⁵

-Procéder à une manière similaire pour trouver le reste des conditions. Voici l'exposant 4:

-5 + 2 + a = 10 → a = 10 + 5-2 = 13

Le terme manquant est: 13X⁴.

-Pour les pouvoirs x³ Il est immédiat que le terme doit être -9x³, De cette façon, le coefficient de terme cube est 0.

-Quant aux pouvoirs carrés: a + 8 -14 = -11 → a = -11 -8 + 14 = -5 et le terme est -5x².

-Le terme linéaire est obtenu par A +8 -14 = -11 → A = -11 + 14 -8 = -5, étant le terme manquant -5x.

-Enfin, le terme indépendant est: 1 -3 + a = -21 → a = -19.

- Exercice 2

Un terrain plat est entouré comme indiqué sur la figure. Trouver une expression pour:

a) le périmètre et

b) sa zone, en termes de longueurs indiquées:

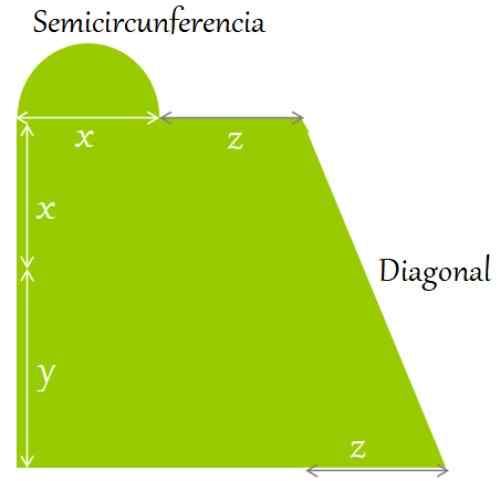Figure 2. Un terrain plat est entouré de la forme et des dimensions indiquées. Source: F. Zapata.

Solution à

Le périmètre est défini comme la somme des côtés et des contours de la figure. En commençant dans le coin inférieur gauche, en direction des mains de l'horloge, vous avez:

Il peut vous servir: trapèze isocèle: propriétés, relations et formules, exemples

Périmètre = y + x + longueur de demi-cercle + z + longueur diagonale + Z + z + x

Le demi-cercle a un diamètre égal à x. Comme le rayon est de la moitié du diamètre, il doit:

Radio = x / 2.

La formule pour la longueur d'une circonférence complète est:

L = 2π x radio

Ensuite:

Longueur de demi-cercle = ½. 2π (x / 2) = πx / 2

Pour sa part, la diagonale est calculée avec le théorème de Pythagore appliqué sur les côtés: (x + y) qui est latérale verticale et z, qui est l'horizontal:

Diagonale = [(x + y)² + z²]]^1/2

Ces expressions sont remplacées dans le périmètre, pour obtenir:

Périmètre = y + x + πx / 2 + z + [(x + y)² + z²]]^1/2+ z + x + z

Des termes similaires sont réduits, car la somme nécessite que le résultat soit simplifié au maximum:

Périmètre = y + [x + π (x / 2) + x] + z + z + z + [(x + y)² + z²]]^1/2 = y + (2 + π / 2) x + 3z

Solution B

La zone résultante est la somme de la zone rectangulaire, le demi-cercle et le triangle droit. Les formules de ces zones sont:

-Rectangle: Base x hauteur

-Demi-cercle: ½ π (radio)²

-Triangle: Base x hauteur / 2

Zone rectangulaire

(x + y). (x + z) = x² + Xz + yx + yz

Zone de demi-cercle

½ π (x / 2)² = π x² / 8

Zone du triangle

½ z (x + y) = ½ zx + ½ zy

Superficie totale

Pour trouver la superficie totale, les expressions trouvées pour chaque zone partielle sont ajoutées:

Zone totale = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

Et enfin tous les termes similaires:

Zone totale = (1 + π / 8) x² + 3/2 xy + 3 / 2yz + yx

Les références

1. Baldor, un. 1991. Algèbre. Éditorial culturel vénézuélien s.POUR.
2. Jiménez, R. 2008. Algèbre. Prentice Hall.
3. Les mathématiques sont amusantes. Ajout de polynômes de soustraction. Récupéré de: Mathsisfun.com.
4. Institut Monterey. Ajout et soustraction de polynômes. Récupéré de: montereyinstitute.org.
5. UC Berkeley. Algèbre des polynômes. Récupéré de: mathématiques.Berkeley.Édu.