Succession composée

Succession composée de carrés jaune et bleu. Source: F. Zapata

Qu'est-ce qu'une succession composite?

Ongle succession composée Il se compose d'une séquence d'éléments, créé à partir de deux (ou plus) successions différentes et alternatives. Chacune de ces successions a une règle particulière, qui est utilisée pour trouver leurs éléments respectifs.

Les éléments ne doivent pas être numériques, pouvoir être des chiffres, des symboles ou des lettres, mais ceux qui sont basés sur des nombres sont appelés successions arithmétiques. La figure avec laquelle notre article commence montre une succession composée des carrés jaunes et bleus.

Dans cette succession, il commence à partir d'un grand carré composé de 8 carrés jaunes et d'un carré bleu. Pour obtenir le terme suivant, un carré jaune est ajouté à la gauche ou à la droite de la première et de la troisième rangée de carrés. L'espace qui se traduit par la ligne centrale est rempli d'un carré bleu.

Chaque figure de la séquence est appelée terme. Si vous souhaitez trouver le cinquième mandat, vous devez ajouter un carré jaune à droite des premier et troisième rangs, et un carré bleu dans la deuxième rangée:

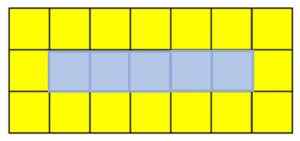Cinquième mandat d'une succession de carrés jaune et bleu. Source: F. Zapata

Explication

Dans les successions composées, les termes sont obtenus en alternant les termes de deux ou plusieurs successions simples indépendantes. Pour mieux comprendre l'idée, elle devrait être examinée les détails d'une simple succession.

Par exemple, la succession simple suivante se compose des nombres naturels:

2, 4, 6, 8, 10, 12 ..

Les points suspendus indiquent que la succession a des termes infinis.

Chacun des termes est indiqué par une petite lettre et un nombre, en indice. Ce nombre indique la position ou indice de chaque terme. Dans la succession précédente, vous pouvez écrire:

pour₁ = 2; pour₂ = 4; pour₃ = 6; pour₄ = 8 ..

Il est très pratique d'avoir un moyen de calculer tout terme souhaité de la succession, c'est-à-dire sa règle particulière. Avec elle le Terme N-ESimo, soit Terme général, indiqué comme un_n.

Peut vous servir: propriétés d'égalité

Poursuivant avec l'exemple de la succession de nombres pair, vous pouvez établir le moyen de calculer le terme N-éimo, à partir du trimestre précédent:

pour_n = A_N-1 + 2

Où_N-1 C'est le terme qui précède_n.

Bien sûr, il serait préférable de connaître le terme général sans dépendre d'autres termes. Dans cette succession, il est facile de noter que tout terme se multiplie par 2 la position qu'il occupe, compte tenu de l'indice du terme. De cette façon, il est écrit:

pour_n = 2n

Les Grecs anciens connaissaient déjà les successions de nombres uniformes et étranges. La succession de nombres naturels étranges, quant à eux, peut être écrit comme:

1, 3, 5, 7, 9, 11 ..

Et combinant la succession des nombres pair avec celui de l'étrange, la succession composée suivante est:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Dont le résultat est l'ensemble des nombres naturels.

Conditions d'une succession composée

Il peut être amusant d'essayer de trouver la relation qui existe dans une séquence de nombres, pour laquelle il doit être soigneusement observé et essayer d'identifier s'il s'agit d'une succession composite.

La forme générale d'une succession composée de deux successions sera:

pour₁, b₁, pour₂, b₂, pour₃, b₃, pour₄, b₄,..

Où₁, pour₂, pour₃, pour₄,... sont les termes de la première succession et b₁, b₂, b₃, b₄,… Ceux de la seconde. Ils sont toujours entrecoupés, comme c'est le cas dans cet exemple:

7, 8, 14, 16, vingt-et-un, 24, 28, 32, 35..

Quel sera le terme qui suit?

Pour savoir, connaître la succession en deux ensembles de nombres alternatifs, comme suit:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

Dans le premier de ces ensembles, les multiples de 7 apparaissent:

pour₁ = 7 × 1 = 7; pour₂ = 7 × 2 = 14; pour₃ = 7 × 3 = 21; pour₄ = 7 × 4 = 28; pour₅ = 7 × 5 = 35

Le terme général de cette succession est:

pour_n = 7n

Et dans le second, ce sont les multiples de 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Son terme général est donc:

Il peut vous servir: vraie fonction variable réelle et sa représentation graphique

b_n = 8n

Revenant à la succession du composé d'origine, le 35 appartient à la première séquence, dont les termes sont à₁, pour₂, pour₃, pour₄ … 35 est le cinquième mandat, donc le terme qui suit doit être b₅, qui est facilement obtenu à partir de la règle pour trouver le terme général:

b₅ = 8 × 5 = 40

Et il est écrit:

7, 8, 14, 16, vingt-et-un, 24, 28, 32, 35, 40 ..

Exemples de successions composites

Exemple 1

Vous pouvez créer une succession composite avec des figures géométriques, telles que le carré et le cercle, les disposant comme indiqué ci-dessous:

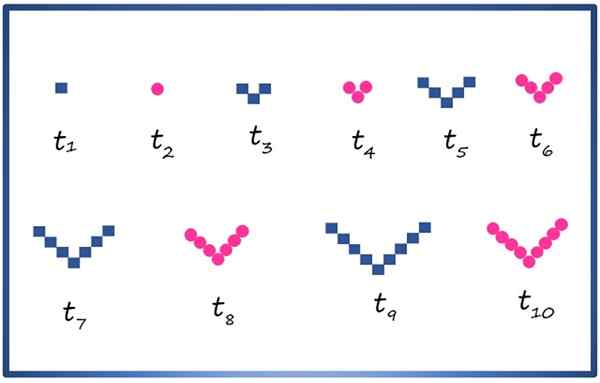Les 10 premiers termes d'une succession composite avec les éléments et cercles géométriques carrés. Source: F. Zapata

Chaque terme est indiqué par t₁, t₂, t₃, t₄ …, Les termes de l'index de parque sont constitués de cercles et de ceux de l'indice étrange, carrés. Observant soigneusement la séquence qu'il est possible de savoir, par exemple, que le terme t_onze, Cela n'apparaît pas dans l'image, se compose de 11 carrés avec la disposition dans V.

Exemple 2

La succession composite suivante se compose de symboles, dans ce cas, les lettres R et S:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSS ..

Chaque nouveau terme est construit en ajoutant une lettre à la précédente. Les quatre premiers termes de la séquence indiquée sont:

t₁= R ; t₂= H.H ; t₃= Rr ; t₄= SSS ..

Et le terme suivant qui apparaîtrait après les termes indiqués est:

t_onze= Rrrrrr

Exemple 3

Les exemples précédents ont montré des successions ascendantes, dans lesquelles chaque valeur augmente, d'une manière ou d'une autre, en ce qui concerne le précédent. Mais il ne doit pas toujours être de cette manière, car les successions peuvent être descendantes, c'est-à-dire qu'ils ont un modèle de diminution.

Et les successions ascendantes peuvent être combinées avec des successions descendantes.

La succession numérique suivante est composée:

4, 36, 7, 35, dix, ___, ___, 33, 16, ___, ___, ..

Il peut être séparé en deux successions:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Quelles sont les valeurs qui doivent être placées dans les espaces vides?

Observant soigneusement la première succession, chaque terme est obtenu en ajoutant 3 au terme précédent. C'est donc une succession ascendante:

Peut vous servir: déplacement angulaire

7 = 4 + 3

10 = 7 + 3

Par conséquent, dans le premier espace vide, vous devez placer:

10 + 3 = 13

Après cela, le terme suivant est en fait:

16 = 13 + 3

Et celui qui va dans le deuxième blanc est:

16 + 3 = 19

La deuxième succession est descendante et il est très facile de trouver les termes manquants, car il est observé que chaque terme est obtenu en soustrayant 1 du terme précédent, donc:

36, 35, 3. 4, 33, 32..

Enfin, vous pouvez écrire:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Exercices résolus

Exercice 1

Dans la succession composée de l'exemple 3 dans la section précédente:

a) appartient 29 à ladite succession?

b) Écrire 10 autres termes de cette succession

Réponds à

Oui il appartient, car la deuxième succession descend et ses termes sont obtenus en soustrayant 1 du terme précédent. De cette façon, il atteint finalement 29.

Réponse b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Notez que certains termes sont répétés.

Exercice 2

Trouvez les termes manquants dans la succession composée suivante:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Répondre

Les termes étranges sont écrits pour obtenir la première succession:

100, 115, 130, 145, 160, ..

Il est observé que, pour trouver chaque terme, vous devez en ajouter 15 au terme précédent, par conséquent, le terme qui suit à 160 est 175.

La deuxième succession se compose de:

500, 480, 460, 440, 420, ..

Chaque terme diffère de la précédente sur 20, la succession étant descendante, par conséquent, le terme suivi à 420 est 400.

Avec ces informations, deux autres termes sont ajoutés à la succession du composé d'origine, comme ceci:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Les références

1. Larson, R. (2012). Précalation. 8e. Édition. Cengage Learning.
2. Stewart, J. (2007). Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
3. Successions composites. Récupéré de: médias.Educacioncampeche.Gueule.mx.
4. Successions numériques. Récupéré de: Matemathweb.com.
5. Succession. Progressions arithmétiques et géométriques. Récupéré de: Macmillaneducation.est.