Système octal

Qu'est-ce qu'un système octal?

Il Système octal Il s'agit d'un système de numérotation de base huit (8); C'est-à-dire qu'il se compose de huit chiffres, qui sont: 0, 1, 2, 3, 4, 5, 6 et 7. Par conséquent, chaque chiffre d'un nombre octal peut avoir n'importe quelle valeur de 0 à 7. Les nombres octaux sont formés à partir de nombres binaires.

C'est parce que sa base est une puissance exacte de deux (2). C'est-à-dire que les nombres appartenant au système octal sont formés lorsqu'ils sont regroupés en trois chiffres consécutifs, ordonnés de droite à gauche, obtenant ainsi leur valeur décimale.

Histoire du système octal

Le système octal a son origine dans les temps anciens, lorsque les gens ont utilisé leurs mains pour compter huit par huit animaux.

Par exemple, pour compter le nombre de vaches dans une stable, la main droite a commencé à avoir le pouce avec le petit doigt; Ensuite, pour compter le deuxième animal, le pouce est venu avec l'index, et ainsi de suite avec les doigts restants de chaque main, jusqu'à ce qu'il termine 8.

Il est possible que le système de numérotation octal avant la décimale puisse compter les espaces interdigitaux; c'est-à-dire dire à tous les doigts à l'exception des pouces.

Par la suite, le système de numérotation octal a été établi, qui provient du système binaire, car il a besoin de nombreux chiffres pour représenter un seul nombre; Dès lors, des systèmes octaux et hexagonaux ont été créés, qui ne nécessitent pas autant de chiffres et qui peuvent facilement se convertir au système binaire.

Système de numérotation octale

Le système octal se compose de huit chiffres allant de 0 à 7. Ceux-ci ont la même valeur que dans le cas du système décimal, mais leur valeur relative change en fonction de la position que celles-ci occupe. La valeur de chaque position est donnée par les pouvoirs de base 8.

Il peut vous servir: règle t: caractéristiques, afin que ce soit, des exemples

Les positions des chiffres dans un nombre octal ont les pesos suivants:

8⁴, 8³, 8², 8¹, 8⁰, Octal Point, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Le chiffre octal majeur est de 7; De cette façon, lorsqu'il est compté dans ce système, une position d'un chiffre de 0 à 7 augmente. Lorsqu'il atteint 7, il est recyclé à 0 pour le décompte suivant; Cela augmente la position de chiffre suivante. Par exemple, pour compter les séquences, dans le système octal, ce sera:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Il existe un théorème fondamental qui est appliqué au système octal et est exprimé comme suit:

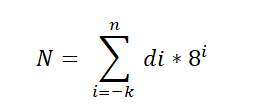
Dans cette expression, DI représente le chiffre multiplié par la puissance de base 8, qui indique la valeur de positionnel de chaque chiffre, de la même manière dont il est ordonné dans le système décimal.

Par exemple, vous avez le numéro 543.2. Pour l'emmener au système octal, il se décompose comme suit:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

De cette façon, vous avez 543.2_q = 354,25_d. L'indice qui indique qu'il s'agit d'un numéro octal qui peut également être représenté par le numéro 8; et l'indice D fait référence au nombre décimal, qui peut également être représenté avec le numéro 10.

Conversion du système octal en décimal

Pour convertir un numéro de système octal en son équivalent en système décimal, chaque chiffre octal doit être multiplié par sa valeur de position, à partir de la droite.

Exemple 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474_dix

Peut vous servir: égalité mathématique

Exemple 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23 125_dix

Conversion du système décimal en octal

Un entier décimal peut être converti en un nombre octal en utilisant la méthode de division répétée, où l'entier décimal est divisé par 8 jusqu'à ce que le quotient soit égal à 0, et le gaspillage de chaque division représentera le nombre octal.

Les déchets sont commandés du dernier au premier; c'est-à-dire que le premier résidu sera le chiffre le moins important du nombre octal. De cette façon, le chiffre le plus important sera le dernier résidu.

Exemple

Octal de la décimale numéro 266_dix

- Le numéro décimal 266 est divisé par 8 = 266/8 = 33 + 2 résidus.

- Alors le 33 est divisé par 8 = 33/8 = 4 + 1 résidu.

- 4 est divisé par 8 = 4/8 = 0 + 4 résidus.

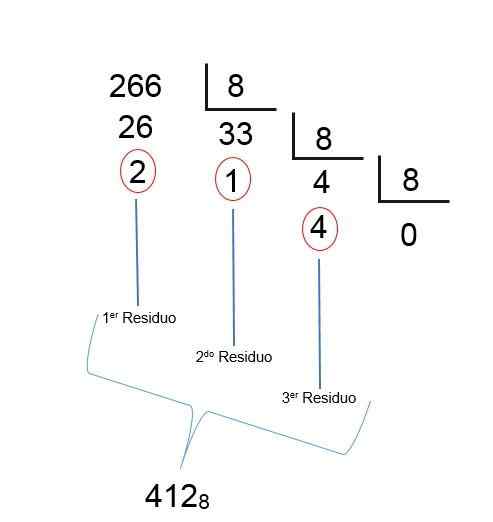
Comme pour la dernière division, un quotient inférieur à 1 est obtenu, cela signifie que le résultat a été trouvé; Seuls les restes doivent être commandés à l'envers, de sorte que le nombre octal de décimal 266 est 412, comme on peut le voir dans l'image suivante:

Conversion du système octal binaire

La conversion de l'octal en système binaire est effectuée lors de la conversion du chiffre octal en son chiffre binaire équivalent, formé par trois chiffres. Il y a une table qui montre comment les huit chiffres possibles deviennent:

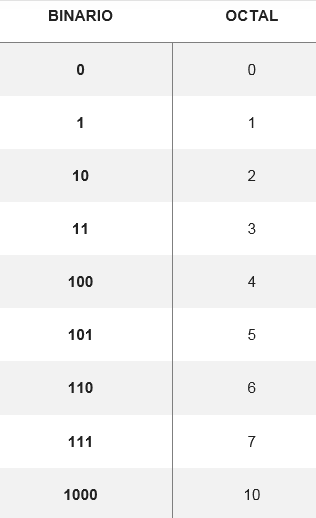
À partir de ces conversions, vous pouvez modifier n'importe quel nombre du système octal en binaire, par exemple pour convertir le numéro 572₈ Vos équivalents sont recherchés dans le tableau. Ainsi, vous devez:

5₈ = 101

7₈= 111

2₈ = 10

Par conséquent, 572₈ équivalent dans le système binaire à 10111110.

Système binaire à conversion octale

Le processus de conversion des nombres intégraux en entiers octaux est le fonctionnement inverse du processus précédent.

Peut vous servir: quels sont les éléments d'un angle?

C'est-à-dire que les bits de nombre binaire sont regroupés en deux groupes de trois bits, de droite à gauche. Ensuite, la conversion binaire à octal est effectuée avec le tableau précédent.

Dans certains cas, le nombre binaire n'aura pas de groupes de 3 bits; Pour le terminer, un ou deux zéros sont ajoutés à gauche du premier groupe.

Par exemple, pour modifier le numéro binaire 11010110 en octal, ce qui suit est effectué:

- Des groupes de 3 bits sont formés à partir de la droite (dernier bit):

11010110

- Comme le premier groupe est incomplet, un zéro est ajouté à gauche:

011010110

- La conversion est effectuée à partir du tableau:

011 = 3

010 = 2

110 = 6

De cette façon, le numéro binaire 011010110 est équivalent à 326₈.

Conversion du système octal en hexadécimal et vice versa

Pour changer un nombre octal en système hexadécimal ou hexadécimal vers le système octal, il est nécessaire que le nombre soit d'abord binaire, puis au système souhaité.

Pour cela, il y a un tableau où chaque chiffre hexadécimal est représenté avec son équivalence dans le système binaire, composé de quatre chiffres.

Dans certains cas, le nombre binaire n'aura pas de groupes de 4 bits; Pour le terminer, un ou deux zéros sont ajoutés à gauche du premier groupe

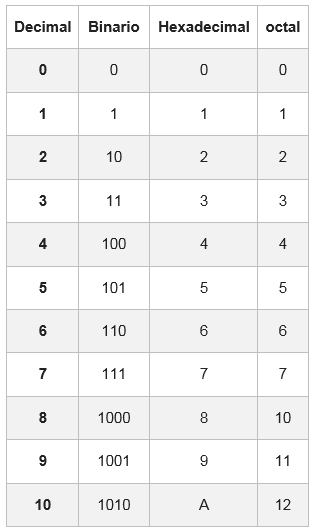
Exemple

Convertir le numéro octal 1646 en un numéro hexadécimal:

- Le nombre octal à binaire devient

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Ainsi, 1646₈ = 1110100110.

- Pour convertir du binaire en hexadécimal, ils sont d'abord ordonnés en groupe de 4 bits, à partir de la droite à gauche:

11 1010 0110

- Le premier groupe est complété avec des zéros, afin qu'il puisse avoir 4 bits:

0011 1010 0110

- La conversion du système binaire hexadécimal est effectuée. Les équivalences sont remplacées au moyen du tableau:

0011 = 3

1010 = A

0110 = 6

De cette façon, le nombre octal de 1646 équivaut à 3A6 dans le système hexadécimal.