Système d'équations Méthodes de solution, exemples, exercices

Les systèmes d'écolation Ils se composent de deux équations ou plus avec plusieurs variables qui doivent avoir une solution commune. Ils sont fréquents, car dans la pratique, il existe de nombreuses situations qui dépendent de nombreux facteurs, qui sont liés de plusieurs manières.

En général, un système d'équations a la forme suivante, où chaque fonction représente l'une des conditions que la solution doit satisfaire:

Figure 1. Un système d'équations se compose de m fonctions et n inconnues. Source: F. Zapata.

Regardons un exemple: Supposons que vous ayez besoin de fabriquer des feuilles de papier rectangulaires dont la zone est de 180 cm² et avoir un périmètre de 54 cm. Quelles devraient être les dimensions de la feuille?

Pour répondre à la question, nous prenons en compte que les dimensions d'une feuille rectangulaire sont deux: large et élevée. Cela signifie que nous avons 2 variables auxquelles nous donnerons les noms habituels de X et et.

Et ces variables doivent satisfaire aux deux conditions imposées en même temps:

-Première condition: la région de la lame est de 180 cm². Ce sera la première fonction: F₁.

-Deuxième condition: le périmètre ou le contour de la feuille doit être de 54 cm. Ceci est la deuxième fonction F₂.

Pour chaque condition, une équation est établie en utilisant un langage algébrique. La zone A d'une feuille rectangulaire est obtenue en multipliant largement:

A = x.y = 180 cm²

Et le périmètre p résulte de l'ajout des côtés. Puisque le périmètre est la somme des côtés:

P = 2x + 2y = 54 cm

Le système résultant de deux équations et de deux inconnues est:

Xy = 180

2 (x + y) = 54

Nous avons besoin de deux chiffres dont le produit est 180 et que le double produit de sa somme est de 54, ou ce qui est le même: ajouté doit donner 27. Ces chiffres sont 12 et 15.

Dans la section des exercices résolus, nous proposerons la méthode détaillée pour trouver ces valeurs, en attendant le lecteur peut facilement vérifier le remplacement, qui satisfait efficacement les deux équations.

[TOC]

Exemples d'applications de systèmes d'équations

La situation proposée ci-dessus contient 2 variables, et au moins 2 équations sont nécessaires pour les trouver. Il existe des systèmes avec beaucoup plus de variables, mais en tout cas, si le système a n Parmi ceux-ci, au moins c'est requis n des équations indépendantes (on ne peut pas être une combinaison linéaire des autres) pour trouver la solution, si elle existe.

Peut vous servir: corde (géométrie): longueur, théorème et exercices

Quant aux applications, ils sont nombreux. Voici quelques-uns dans lesquels les systèmes d'équations démontrent leur utilité:

-Trouvez les courants qui circulent à travers un circuit au moyen des lois de Kirchoff.

-Dans le transport terrestre et aérien pour établir les horaires de sortie et d'arrivée.

-Trouvez les amplitudes des forces dans les systèmes dynamiques ou statiques soumis à de multiples interactions.

-Pour connaître la quantité d'articles vendus pendant une certaine période de temps, ou dans les usines, pour déterminer les dimensions des objets pour satisfaire à certaines conditions en termes de surface ou de volume.

-Lors de la détermination de la façon de distribuer un capital en plusieurs investissements.

-Établir des tarifs pour divers services, par exemple des télécommunications ou des spectacles et connaissez le montant d'argent perçu (voir l'exemple résolu 2)

Méthodes de solution des systèmes d'équations

Méthode de remplacement

-Une équation est choisie et l'une des variables est effacée.

-Alors vous devez remplacer la variable claire dans une autre équation. Alors cette variable disparaît de là et si le système a deux équations et deux inconnues, il existe une équation avec une variable qui peut déjà être claire.

-Si le système a plus de deux variables, vous devez effacer une troisième inconnue d'une autre équation et la remplacer également.

Un exemple d'application de cette méthode est de l'année résolue 1.

Méthode de réduction ou d'élimination

Cette méthode consiste à ajouter ou à soustraire des équations pour éliminer une ou plusieurs variables et laisser un seul. Pour ce faire, il est pratique de multiplier les équations par un facteur tel qu'en ajoutant avec une autre équation, l'inconnu disparaît. Regardons un exemple:

3x² - et² = 11

Peut vous servir: mesures de tendance centrale pour les données groupées: formules, exercices

X² + 4Y² = 8

Nous multiplions la première équation par 4:

12X² - 4Y² = 44

X² + 4Y² = 8

En leur ajoutant l'inconnu disparaître et, rester:

13X² = 52

X² = 4

Par conséquent X₁ = 2 et x₂ = -2. Avec ces valeurs, le lecteur peut vérifier cela et₁ = 1 et₂ = -1

Méthode d'égalisation

Lorsque le système est de deux équations avec deux inconnues:

-Une inconnue est choisie et des clairs des deux équations.

-Les résultats sont égalisés, ce qui permet d'obtenir une seule équation avec un seul inconnu.

-Cette équation est résolue et le résultat est remplacé dans l'une des clairières précédentes pour obtenir la valeur de l'autre inconnue.

Cette méthode sera appliquée dans l'année résolue 2 de la section suivante.

Méthode graphique

Cette méthode consiste à représenter graphiquement les courbes que chaque équation représente. Le point d'intersection est la solution système. L'exemple suivant montre la solution graphique du système:

X² + et ² = 1

2x + 4y = 0

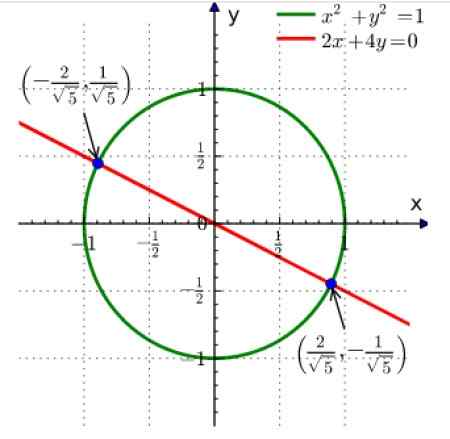Figure 2. La solution graphique du système d'équations simultanées est de trouver l'intersection des courbes. Source: Wikimedia Commons.

Le premier des équations est un cercle de rayon 1 axé sur l'origine et le second est une ligne.

L'intersection des deux est les deux points montrés en bleu. Le lecteur peut vérifier qu'en remplaçant les coordonnées des points dans les équations ci-dessus, une égalité est obtenue.

Exercices

- Exercice résolu 1

Vous devez fabriquer des feuilles rectangulaires de 180 cm de zone² Et avec un périmètre de 54 cm. Quelles devraient être les dimensions de la feuille?

Solution

Le système à résoudre est:

Xy = 180

2 (x + y) = 54

La deuxième équation peut être simplifiée en x + y = 27, donc:

Xy = 180

x + y = 27

L'une des inconnues de la deuxième équation est effacée:

y = 27 - x

Le dégagement est remplacé dans le premier:

(27 -x) = 180

Application de biens distributifs:

-X² + 27x = 180

Multipation de (-1) des deux côtés de l'équation et envoyant 180 sur le côté gauche:

X² - 27x +180 = 0

Il s'agit d'une équation du deuxième degré en x, qui est résolue par la formule:

Il peut vous servir: angles opposés par le sommet (avec un exercice résolu)

Avec a = 1, b = -27 et c = 180

 Les solutions sont: x₁ = 15 cm et x₂ = 12, donc les dimensions de y sont et₁ = 12 cm et et₂ = 15 cm.

- Exercice résolu 2

Un parc d'attractions a les taux suivants par entrée: enfants 1.5 et adultes 4 $. En une journée, il y avait 2200 visiteurs, levant 5050 $. Trouvez le nombre d'enfants et d'adultes qui ont visité le parc ce jour-là.

figure 3. Le système d'équations sert à briser la collecte du parc d'attractions en une journée. Source: Pixabay.

Solution

Être X Le nombre d'enfants et et Le nombre d'adultes. Nous pouvons établir la première des équations sachant que la somme des deux doit être de 2200:

x + y = 2200.

Maintenant, nous allons avec l'argent collecté. Le prix du billet pour les enfants est 1.5 $ Pour chaque enfant, en multipliant cette valeur par x, le nombre d'enfants, nous aurons le montant de l'entrée des enfants:

1.5x = argent collecté par les billets pour enfants

Et si nous multiplions 4 $ par adulte pour la quantité et les visiteurs adultes, l'argent total est obtenu par tous les adultes:

4y = argent collecté par les billets pour adultes

Nous l'ajoutons pour obtenir 5050 $:

1.5x + 4y = 5050

Notre système d'équations est:

x + y = 2200

1.5x + 4y = 5050

Résolvons-le par égalisation. Nous effacons la variable et la première et la deuxième équation:

y = 2200 - x

y = (5050 - 1.5 x) / 4

Nous égalons les deux expressions:

2200 - x = (5050 - 1.5x) / 4

Nous multiplions tout par 4 pour éliminer la fraction:

8800 - 4x = 5050 - 1.5x

Nous regroupons les termes avec x à gauche et les nombres purs à droite:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 enfants.

Nous remplaçons cette valeur à y = 2200 - x pour connaître le nombre d'adultes:

y = 2200 - 1500 = 700 adultes.

Les références

1. CK-12. Systèmes d'équations et d'inégalités. Récupéré de: CK12.org.
2. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
3. Jiménez, R. 2008. Algèbre. Prentice Hall.
4. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.