Demi-cercle Comment calculer le périmètre, la zone, le centroïde, les exercices

Il demi-cercle C'est une figure plate délimitée par un diamètre de la circonférence et l'une des deux arches circulaires plates déterminées par ledit diamètre.

De cette façon, un demi-cercle est bordé par un semi-circumaison, qui se compose d'un arc circulaire plat et d'un segment droit qui rejoint les extrémités de l'arc circulaire plat. Le demi-cercle couvre le demi-cercle et tout l'intérieur pointe vers le même.

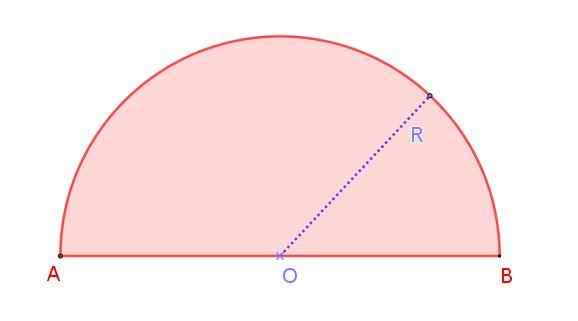Figure 1. Radio R Radio Semiccle. Source: F. Zapata.

Nous pouvons le voir dans la figure 1, qui montre une radio r rión r, dont la mesure est la moitié du diamètre AB. Notez que contrairement à un cercle, dans lequel il y a des diamètres infinis, en demi-cercle, il n'y a qu'un seul diamètre.

Le demi-cercle est une figure géométrique avec de nombreuses utilisations dans l'architecture et la conception, comme nous le voyons dans l'image suivante:

Figure 2. Seminicírculo comme élément décoratif de l'architecture. Source: Pikist.

[TOC]

Éléments et mesures d'un demi-cercle

Les éléments d'un demi-cercle sont:

1.- L'arc circulaire plat a⌒b

2.- Le segment [AB] 

3.- L'intérieur pointe vers un demi-cercle composé de l'arc et du segment A⌒B [AB].

Périmètre d'un demi-cercle

Le périmètre est la somme du contour de l'arc plus celle du segment droit, donc:

Périmètre = longueur d'arc a⌒b + longueur de segment [AB]

Dans le cas d'un demi-cercle radio r, son périmètre P sera donné par la formule:

P = π⋅r + 2⋅r = (π + 2) ⋅r

Le premier terme est la moitié du périmètre d'une circonférence de rayon R, tandis que la seconde est la longueur du diamètre, qui est deux fois le rayon.

Peut vous servir: échelles thermométriques

Zone d'un demi-cercle

En tant que demi-cercle est l'un des secteurs angulaires plats qui restent en dessinant un diamètre à travers la circonférence, sa zone A sera la moitié de la zone du cercle qui contient le demi-cercle radio R:

A = (π⋅r²) / 2 = ½ π⋅r²

Centroïde d'un demi-cercle

Le centroïde d'un demi-cercle est sur son axe de symétrie à une hauteur mesurée de son diamètre de 4 / (3π) fois le rayon R.

Cela correspond à environ 0,424⋅r, mesuré à partir du centre du demi-cercle et sur son axe de symétrie, comme le montre la figure 3.

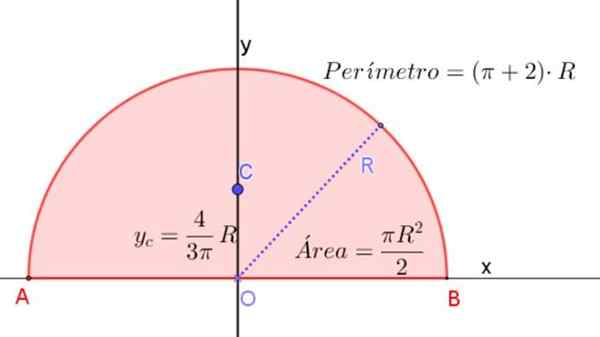figure 3. Demi-cercle de radio R, indiquant les formules pour déterminer la zone, le périmètre et l'emplacement de son centroïde. Source: F. Zapata.

Moment d'inertie d'un demi-cercle

Le moment d'inertie d'une figure plate est défini par rapport à un axe, par exemple l'axe x, tel que:

L'intégrale du carré de la distance des points qui appartiennent à la figure à l'axe, le différentiel d'intégration étant une zone infinitésimale de zone, prise en position de chaque point. 

La figure 4 montre la définition du moment de l'inertie I_X du demi-cercle de radio r, par rapport à l'axe x qui passe par sa diagonale:

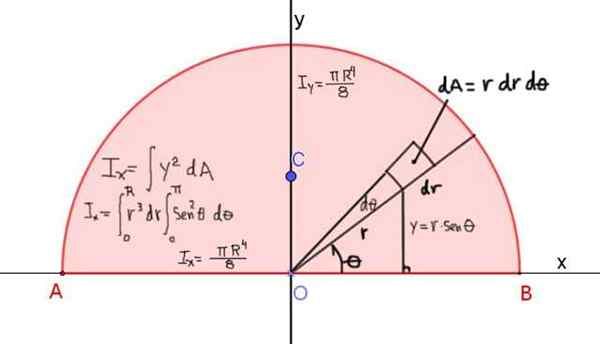Figure 4. Définition du moment d'inertie ix d'un demi-cercle par rapport à l'axe x qui passe par sa diagonale. Le résultat est indiqué pour les moments d'inertie par rapport aux axes x et y. Source: F. Zapata.

Le moment d'inertie par rapport à l'axe x est donné par:

Toi_X = (π⋅r⁴) / 8

Et le moment d'inertie par rapport à l'axe de symétrie et est:

Peut vous servir: optique ondulée

Iy = (π⋅r⁴) / 8

Cela montre que les deux moments d'inertie coïncident dans leur formule, mais il est important de souligner qu'ils sont référés à différents axes.

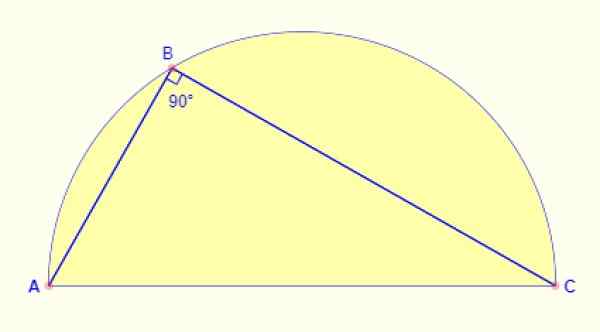
Angle enregistré

L'angle enregistré en demi-cercle est toujours à 90º. Quelle que soit la partie de l'arc est prise vers le point, l'angle qui se forme entre les côtés AB et la Colombie-Britannique de la figure est toujours droit.

Figure 5. Angle enregistré en demi-cercle. Source: Math Open Reference.

Exercices résolus

Exercice 1 

Déterminer le périmètre d'un demi-cercle de rayon de 10 cm.

Solution

Rappelons que le périmètre en fonction du rayon est donné par la formule que nous avons vue précédemment:

P = (2 + π) ⋅r

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Exercice 2

Trouvez la zone d'un demi-cercle radio de 10 cm.

Solution

La formule de la zone d'un demi-cercle est:

A = ½ π⋅r² = ½ π⋅ (10 cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Exercice 3

Déterminez la hauteur h du centroïde d'un demi-cercle de rayon r = 10 cm mesuré à partir de sa base, le même étant le diamètre du demi-cercle. 

Solution

Le centroïde est le point d'équilibre des demi-cercles et sa position est sur l'axe de symétrie à une hauteur h de la base (diamètre de demi-cercle):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4 246 cm

Exercice 4

Trouvez le moment d'inertie d'un demi-cercle par rapport à l'axe qui coïncide avec son diamètre, sachant que le demi-cercle est fait d'une feuille mince. Son rayon est de 10 cm et sa masse est de 100 grammes.

Solution

La formule qui donne le moment d'inertie du demi-cercle est:

Peut vous servir: physique à l'état solide: propriétés, structure, exemples

Toi_X = (π⋅r⁴) / 8

Mais comme le problème nous dit qu'il s'agit d'un demi-cercle de matériau, la relation précédente doit être multipliée par la densité de surface de la masse de demi-cercle, qui sera indiquée par σ.

Toi_X = σ (π⋅r⁴) / 8

Nous déterminons ensuite σ, qui n'est rien d'autre que la masse du demi-cercle divisé entre la zone de la même.

La zone a été déterminée dans l'exercice 2 et le résultat était de 157 cm². Ensuite, la densité superficielle de ce demi-cercle sera:

σ = 100 grammes / 157 cm² = 0,637 g / cm²

Ensuite, le moment d'inertie par rapport au diamètre sera calculé comme suit:

Toi_X = (0,637 g / cm²) [3 1416 ⋅ (10 cm)⁴] / 8

Donnant comme résultat:

Toi_X = 2502 g⋅cm²

Exercice 5

Déterminez le moment d'inertie d'un demi-cercle de rayon 10 cm construit d'une feuille de matériau avec une densité de surface de 0,637 g / cm² par un axe qui passe par son centroïde et est parallèle à son diamètre.

Solution

Pour résoudre cet exercice, il est nécessaire de se souvenir du théorème de Steiner sur des moments d'inertie des axes parallèles, qui dit:

Le moment d'inertie I par rapport à un axe qui est à une distance h du centroïde est égal à la somme du moment d'inertie i_c Concernant un axe qui passe par le centroïde et est parallèle au premier le produit de la pâte à travers le carré de la séparation des deux axes.

I = i_c + M h²

Dans notre cas, il est connu que c'est le moment de l'inertie par rapport au diamètre, qui a déjà été calculé dans l'exercice 4. H sait également entre le diamètre et le centroïde, qui a été calculé dans l'exercice 3.

Il nous suffit d'effacer IC:

Toi_c = I - m h²

Toi_c = 2502 g⋅cm² - 100 g ⋅ (4 246 cm)² entraînant le moment de l'inertie par un axe parallèle au diamètre et qui passe par le centroïde est: 

Toi_c = 699.15 g⋅cm²

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Référence ouverte en mathématiques. Demi-cercle. Récupéré de: MathpenRef.com.
3. Formules d'univers.Demi-cercle. Récupéré de: universoformules.com.
4. Formules d'univers. Zone d'un demi-cercle. Récupéré de: universoformules.com.
5. Wikipédia. Demi-cercle. Récupéré de: dans.Wikipédia.com.