Règle des Sturges

Nous expliquons quelle est la règle Sturges, son application et donnons plusieurs exemples

Quelle est la règle Sturges?

La Règle des Sturges Il s'agit d'un critère utilisé pour déterminer le nombre de classes ou d'intervalles nécessaires pour représenter graphiquement un ensemble de données statistiques. Cette règle a été indiquée en 1926 par le mathématicien allemand Herbert Sturges.

Sturges a proposé une méthode simple, basée sur le nombre d'échantillons x qui a permis de trouver le nombre de classes et leur gamme de plage. La règle Sturges est largement utilisée avant tout dans la zone statistique, en particulier pour construire des histogrammes de fréquence.

Explication

La règle Sturges est une méthode empirique largement utilisée dans les statistiques descriptives pour déterminer le nombre de classes qui doivent exister dans un histogramme de fréquence, afin de classer un ensemble de données qui représentent un échantillon ou une population.

Fondamentalement, cette règle détermine la largeur des conteneurs graphiques, les histogrammes de fréquence.

Pour établir sa règle, Herbert Sturges a considéré comme un diagramme de fréquence idéal, qui se compose de k intervalles, où l'intervalle I -cte contient un certain nombre d'échantillons (i = 0,… k - 1), représenté comme:

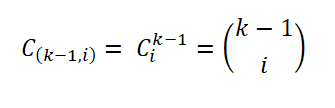
Ce nombre d'échantillons est donné par le nombre de façons dont un sous-ensemble d'un ensemble peut être extrait; c'est-à-dire par le coefficient binomial, exprimé comme suit:

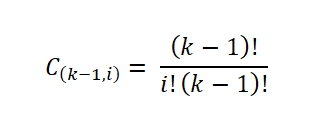Ensuite, Sturges a raconté que l'histogramme de fréquence se rapprochera d'une distribution normale lorsque le nombre d'intervalles (k) augmente en fonction du théorème central de la limite. De telle manière que le nombre d'échantillons de chacun des intervalles peut être calculé:

Il peut vous servir: enegon: propriétés, comment faire une égon, exemples

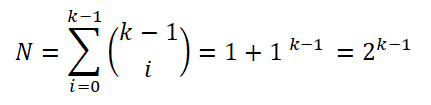
Pour simplifier l'expression, il a appliqué les propriétés des logarithmes dans les deux parties de l'équation:

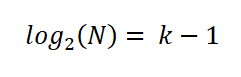
Ainsi, Sturges a établi que le nombre optimal d'intervalles K est donné par l'expression:

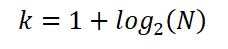
Il peut également être exprimé comme:

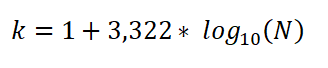
Dans cette expression:

• K est le nombre de classes.
• N est le nombre total d'observations dans l'échantillon.
• Le journal est le logarithme de base commun 10.

Par exemple, pour élaborer un histogramme de fréquence qui exprime un échantillon aléatoire de la stature de 142 enfants, le nombre d'intervalles ou de classes que la distribution aura est:

K = 1 + 3 322 _* enregistrer_dix (N)

K = 1 + 3 322_* Journal (142)

K = 1 + 3 322_* 2 1523

K = 8,14 ≈ 8

Ainsi, la distribution sera à 8 intervalles.

Le nombre d'intervalles doit toujours être représenté par des nombres entiers. Dans les cas où la valeur est décimale, une approximation doit être faite au nombre le plus proche.

Applications de règles Sturges

La règle Sturges est appliquée principalement dans les statistiques, car elle permet une distribution de fréquence à travers le calcul du nombre de classes (k), ainsi que la durée de chacun, également appelée amplitude.

L'amplitude est la différence dans la limite supérieure et inférieure de la classe, divisée par le nombre de classes, et est exprimée:

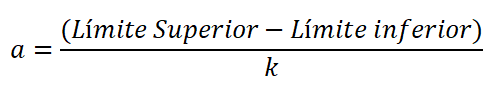
Il existe de nombreuses règles empiriques qui permettent une distribution de fréquence. Cependant, la règle Sturges est couramment utilisée car elle fait une approximation du nombre de classes, qui passe généralement de 5 à 15.

De cette façon, il considère une valeur qui représente correctement un échantillon ou une population; C'est-à-dire que l'approche ne représente pas des groupes extrêmes, et il ne fonctionne pas avec un nombre excessif de classes qui ne permettent pas de résumer l'échantillon.

Il peut vous servir: angles opposés par le sommet (avec un exercice résolu)

Exemple

Un histogramme de fréquence doit être effectué selon les données données, qui correspondent aux âges obtenus dans une enquête auprès des hommes qui font de l'exercice dans un gymnase local.

Pour déterminer les intervalles, la taille de l'échantillon ou le nombre d'observations doivent être connues; Dans ce cas, il y en a 30.

Ensuite, la règle Sturges s'applique:

K = 1 + 3 322 _* enregistrer_dix (N)

K = 1 + 3 322_* Journal (30)

K = 1 + 3 322_* 1 4771

K = 5,90 ≈ 6 intervalles.

D'après le nombre d'intervalles, vous pouvez calculer l'amplitude qu'ils auront; c'est-à-dire la largeur de chaque barre représentée dans l'histogramme de fréquence:

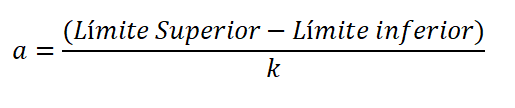
La limite inférieure est considérée comme la valeur inférieure des données, et la supérieure est la valeur la plus élevée. La différence entre la limite supérieure et inférieure est appelée plage ou voie de la variable (R).

Le tableau a que la limite supérieure est de 46 et les 13 inférieurs; De cette façon, l'amplitude de chaque classe sera:

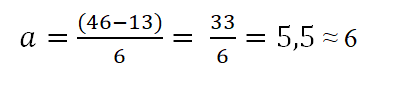
Les intervalles seront composés d'une limite supérieure et inférieure. Pour déterminer ces intervalles, il commence par compter à partir de la limite inférieure, ajoutant à cela l'amplitude déterminée par la règle (6), comme suit:

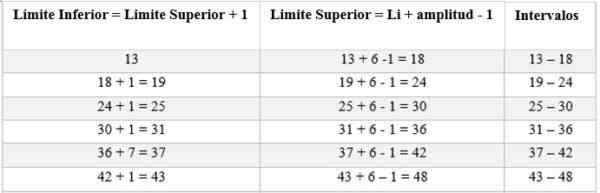
Ensuite, la fréquence absolue est calculée pour déterminer le nombre d'hommes qui correspondent à chaque intervalle; Dans ce cas, c'est:

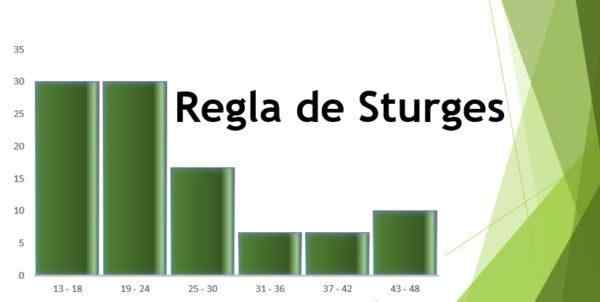
• Intervalle 1: 13 - 18 = 9
• Intervalle 2: 19 - 24 = 9
• Intervalle 3: 25 - 30 = 5
• Intervalle 4: 31 - 36 = 2
• Intervalle 5: 37 - 42 = 2
• Intervalle 6: 43 - 48 = 3

En ajoutant la fréquence absolue de chaque classe, cela doit être égal au nombre total de l'échantillon; Dans ce cas, 30.

Peut vous servir: homotecia négative

Par la suite, la fréquence relative de chaque intervalle est calculée, divisant la fréquence absolue de cela par le nombre total d'observations:

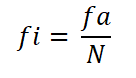
• Intervalle 1: fi = 9 ÷ 30 = 0,30
• Intervalle 2: fi = 9 ÷ 30 = 0,30
• Intervalle 3: fi = 5 ÷ 30 = 0,1666
• Intervalle 4: fi = 2 ÷ 30 = 0,0666
• Intervalle 5: fi = 2 ÷ 30 = 0,0666
• Intervalle 4: fi = 3 ÷ 30 = 0,10

Ensuite, vous pouvez faire un tableau qui reflète les données, ainsi que le diagramme de la fréquence relative par rapport aux intervalles obtenus, comme on peut le voir dans les images suivantes:

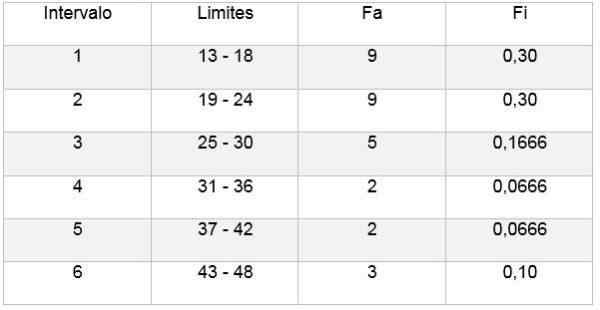
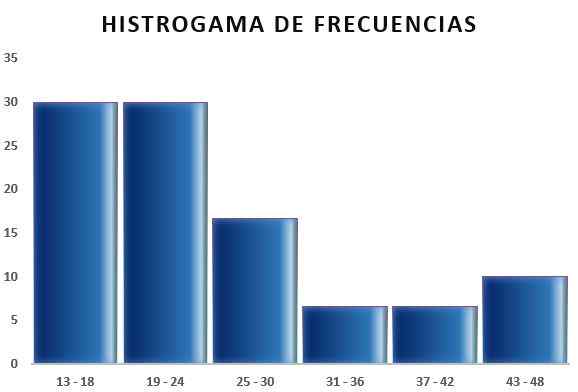
De cette façon, la règle Sturges permet de déterminer le nombre de classes ou d'intervalles dans lesquels un échantillon peut être divisé, afin de résumer un échantillon de données par l'élaboration de tables et de graphiques.