Règle de correspondance d'une fonction

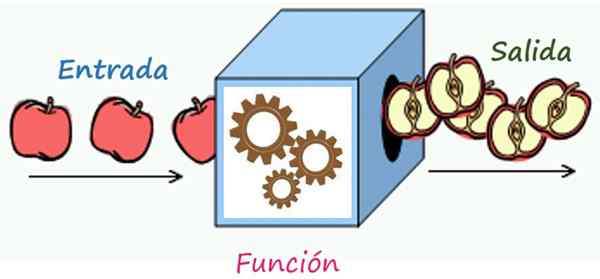La règle de correspondance est un mécanisme qui transforme les éléments de l'entrée en éléments de sortie. Source: Wikimedia Commons / F. Zapata

Quelle est la règle de correspondance d'une fonction?

La Règle de correspondance d'une fonction Souligner la façon dont les éléments d'un ensemble sont liés aux éléments d'un autre. Les éléments du premier ensemble sont connus sous le nom de domaine, Et à ceux de la seconde, comme le Codominium soit contradominium.

La relation ou le lien entre les ensembles peut être spécifié par instruction verbale ou écrite, cependant, lorsque les ensembles sont numériques, la règle de correspondance est indiquée par une formule.

Cette formule contient les opérations qui doivent être effectuées avec les éléments de l'assemblage de départ, et donc obtenir une série d'éléments inclus dans le codominium.

Maintenant, lorsque la relation entre les éléments est une fonction, la règle de correspondance remplit deux conditions spéciales:

• À chacun des éléments du domaine est associé, à travers la règle de correspondance, un seul élément de la codominium, connu sous le nom de image.
• Cette image est unique, en d'autres termes, aucun élément du domaine n'est associé à plus d'un élément de codominium.

De cette façon, vous pouvez imaginer la règle de correspondance d'une fonction en tant que mécanisme verrouillé dans une boîte. Chaque valeur de domaine, sans exception, peut entrer dans la case et en sortir transformé, à travers les opérations indiquées par la règle de correspondance. Les exemples seront vus immédiatement.

Exemples

Exemple 1

La règle de correspondance d'une fonction peut être exprimée comme une instruction écrite, lorsque les éléments ne sont pas numériques.

Par exemple, il existe un ensemble de pays, indiqué comme P, et un autre ensemble de villes C:

Il peut vous servir: U -Test de Mann - Whitney: Qu'est-ce que c'est et lorsqu'il est appliqué, exécution, exemple

P = Canada, Mexique, Espagne, États-Unis, France, Argentine, Brésil, Allemagne

C = Paris, Londres, Buenos Aires, Berlin, Mexico, Ottawa, Río, New York, Madrid, Washington, Berne, Rome, Brasilia, Toronto

Être la règle de correspondance F Entre P et C donné par:

F: P → C

Où F C'est la règle "... dont la capitale est .. », Qui associe chaque pays en p (le set de départ), avec sa capitale en C (l'ensemble d'arrivée).

Par exemple: «Espagne, dont la capitale est Madrid". L'élément "Espagne" appartient à l'ensemble P de départ et à l'élément "Madrid" à l'ensemble C, l'arrivée.

La représentation de cette fonction peut être effectuée via un diagramme de Venn ou simplement à travers des paires ordonnées.

Les paires commandées contiennent, comme son nom l'indique, deux éléments avec un ordre spécifique, dans cet exemple, le premier élément de la paire est le pays, et le second, sa capitale.

Pour sa part, le diagramme de Venn est un moyen de visualiser la fonction, montrant les ensembles de démarrage et d'arrivée, ainsi que la règle de correspondance entre eux.

Représentation de F en paires ordonnées

F = (Canada, Ottawa); (Mexique, Mexique); (Espagne Madrid); (États-Unis; Washington); (Paris, France); (Argentine Buenos Aires); (Brésil Brasilia); (Allemagne, Berlin)

La première paire associée au Canada, dont la capitale est Ottawa, le deuxième associé au Mexique, dont la capitale est Mexico et ainsi de suite.

Représentation de F en tant que diagramme de Venn

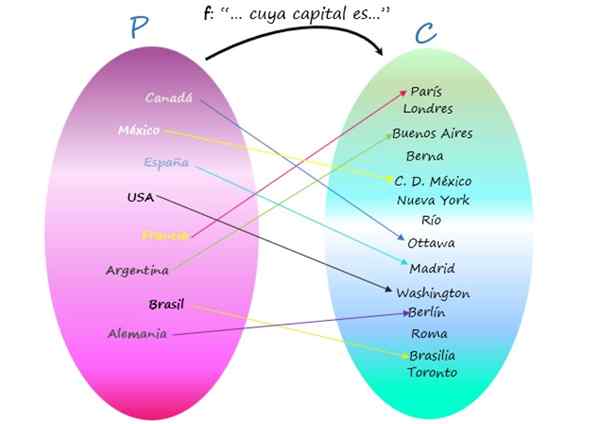
Notez qu'il y a des villes qui ne sont pas la capitale d'un pays, car, bien que ce soient des éléments de la codominium, ils ne sont une image d'aucun élément de l'ensemble de départ. Même ainsi, la relation est une fonction, car l'important est que chaque pays a son capital, et c'est unique.

Peut vous servir: zone d'un pentagone régulier et irrégulier: comment il est pris, exerce

Le sous-ensemble formé par les éléments du codominium qui sont l'image d'un élément du domaine, est appelé plage ou fonction de la fonction. Pour l'exemple, la route R de F est:

R = Paris, Buenos Aires, Mexico, Ottawa, Madrid, Berlin, Washington, Brasilia

Il vaut la peine de demander si une relation entre C et P peut être établie, où C devient l'ensemble de départ et l'arrivée. La réponse est oui, mais ce ne serait pas une fonction, car il y a des villes qui ne sont pas des capitales, comme New York, ou le pays dont ils sont le capital ne figure pas parmi les éléments du complexe P, comme Rome.

Exemple 2

Lorsque l'ensemble de départ et l'ensemble d'arrivée sont numériques, la règle de correspondance de la fonction qui les relie est une formule. Par exemple, soyez la maîtrise d'une fonction l'ensemble suivant:

D = 0, 1, 2, 3, 4, 5, 6)

La règle de correspondance F: D → R qui relie les éléments de D avec l'ensemble des nombres réels R est:

F: "Double"

Si «x» est un élément de l'ensemble de départ, F (x) est l'élément correspondant de l'ensemble d'arrivée, et la règle de correspondance est écrite comme celle-ci:

f (x) = 2x

La codominium est l'ensemble des nombres réels. Un sous-ensemble de la reais est l'itinéraire de cette fonction, l'ensemble des nombres dont la valeur est deux fois comme x:

R = 0, 2, 4, 6, 8, 10, 12

Sous la forme de paires ordonnées, la règle de correspondance se traduit:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Les paires commandées peuvent être graphiques sur le plan cartésien. Le premier élément du couple est placé sur l'axe horizontal, également appelé l'axe des abscisses ou l'axe "x", tandis que le second va sur l'axe vertical, l'axe de l'axe ordonné ou simplement "y":

Peut vous servir: propriété distributive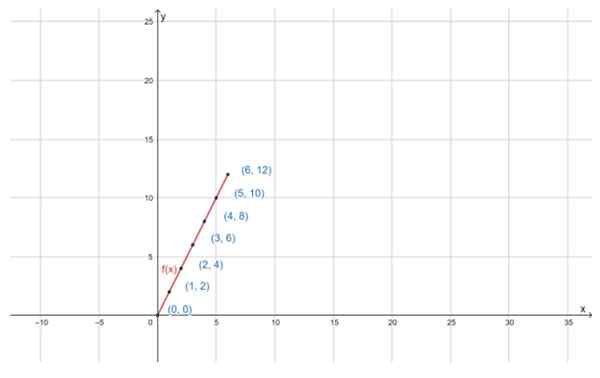 Le graphique de la fonction f (x) = 2x, pour le domaine D spécifié, est une ligne droite. Source: F. Zapata à travers Geogebra

Exercices

Déterminez la règle de correspondance pour les relations suivantes, indiquant si ce sont ou non des fonctions. L'ensemble des nombres naturels est n et celui du réel est r.

Indiquez également le domaine, le codominium et la route de la fonction, dans les cas dans lesquels il correspond:

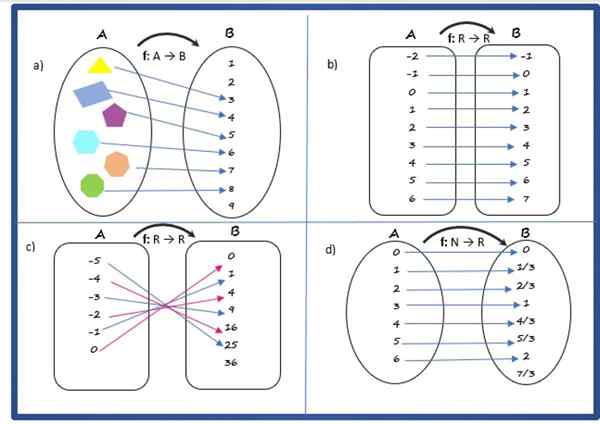
Solution à

C'est une fonction, car chaque élément de l'ensemble de départ, composé de polygones, a une image unique dans l'ensemble d'arrivée.

La règle de correspondance relie le polygone au nombre de ses côtés, le domaine se compose de l'ensemble A des polygones:

A = triangle, quadrilatère, pentagone, hexagone, heptagon, octogone

Le codominium est l'ensemble des premiers nombres naturels, y compris 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Et les co C sont les nombres naturels de 3 à 8:

C = 3, 4, 5, 6, 7, 8

Solution B

C'est une fonction, car il remplit les conditions spécifiées ci-dessus.

La règle de correspondance est:

f (x) = x + 1

La règle de correspondance indique que la fonction est définie par R → R, par conséquent, le domaine est l'ensemble des nombres réels. Et le co-ooominium et l'itinéraire coïncident également avec le réel.

Solution C

C'est une fonction, avec la règle de correspondance:

f (x) = x²

Le domaine et la codominium sont définis de reais, mais l'itinéraire ne se compose que de nombres réels positifs, désignés R⁺ et y compris 0.

Solution d

C'est une fonction. Sa règle de correspondance est:

f (x) = x / 3

Son domaine est l'ensemble des nombres naturels n et codominium, ainsi que l'itinéraire, sont les n nombres N réels R.