Deuxième ligne

Le bois de la porte de ce jardin est disposé de telle manière qu'ils déterminent les lignes sèches. Source: F. Zapata. Pxhere.com

Quelles sont les lignes sèches?

Dans l'avion, le Deuxième ligne Ce sont ceux qui coupent d'autres lignes et courbes. Dans le cas de deux lignes, son intersection est un point, tandis que la ligne sécante à une courbe, le coupe en deux points ou plus.

Observez soigneusement la clôture de la figure supérieure. Il a été dessiné plusieurs couleurs droites droites, dénotées comme L₁, L₂ et moi₃. Les flèches des deux côtés signifient que les lignes sont prolongées indéfiniment.

Eh bien, les lignes L₁, L₂ et moi₃ Ils se séchent, car chaque paire d'entre elles est coupée à des points violets.

De plus, les lignes L₁ et moi₂, Comme L₁ et moi₃, Ils déterminent 4 angles les uns avec les autres, dont deux aigus et l'autre obtus, tandis que les lignes L₂ et moi₃ Ils sont perpendiculaires, ce qui signifie que les 4 angles déterminés par eux sont droits.

Deux lignes parallèles ne peuvent jamais être sèches, car, en raison de leur état, ils n'ont pas de points de coïncidence. À leur tour, les lignes coïncidentes ne sont pas sèches, car elles ont plus d'un point en commun.

Caractéristiques des lignes de séchage

• Deux lignes sécantes ont un point unique comme intersection.
• Les pentes de deux lignes de séchage doivent être différentes. Oui m₁ C'est la pente de la ligne L₁, et M₂ C'est la pente de la ligne L₂, Ensuite, il est accompli que m₁ ≠ m₂.
• Les pentes de deux lignes de séchage perpendiculaires l'une à l'autre, dont les pentes respectives sont m₁ et M₂, Ils accomplissent la relation m₁ = -1 / m₂. De plus, le produit scalaire entre deux vecteurs V et ou contenu dans ces lignes est nul, car la définition du produit scalaire est V ou = v ∙ u ∙ cos θ, étant θ l'angle entre les vecteurs.
• Une ligne peut être sécante à une courbe ou à une autre figure géométrique.
• Lors de leur croisement, deux lignes de séchage génèrent 4 angles, identiques deux à deux ou identiques.

Peut vous servir: équations fractionnaires

Comment savoir si deux lignes sont sèches

D'après les caractéristiques des lignes de séchage décrites ci-dessus, il est possible d'établir trois critères pour savoir si deux lignes sont sèches:

-Comparaison des pentes. Si ceux-ci sont différents, les lignes sont sèches.

-Effectuer le produit scalaire entre deux vecteurs contenus dans ces lignes, appelés Réalisateurs. Si le produit scalaire est vide, les lignes sont sèches et perpendiculaires, et si elle n'est pas-zéro, il est possible de connaître l'angle minimum entre eux, qui est l'angle aigu existant entre les lignes.

À condition que cet angle soit différent de 0º, les lignes sont sèches, et si elle est égale à 0º, alors ce sont des lignes parallèles.

-Calculant directement l'angle aigu qui existe parmi les lignes, connaît leurs pentes. Cela peut être fait à travers la formule qui relie la tangente dudit angle avec les pentes.

Laisse moi₁ et M₂ les pentes, et θ l'angle aigu entre eux. La tangente de θ est donnée par:

Types de lignes de séchage

Lorsque deux lignes se sèchent, elles peuvent être les types suivants:

• Oblique, Si lors de la coupe, ils forment deux angles aigus et deux angles obtus. Ces angles sont supplémentaires, c'est-à-dire que la somme de la mesure de l'angle plus celle de l'angle obtus est égale à 180º. Au total, la somme des 4 angles est égale à 360º.
• Perpendiculaire, Ceux qui se croisent 4 angles égaux à 90º.

Comment trouver l'intersection entre deux lignes

Si deux lignes séchent, elles n'ont qu'un seul point de coupe, qui résout le système de deux équations linéaires avec deux inconnues. Si les lignes sont données en général: AX + BY = C, ledit système d'équations est:

Peut vous servir: ensemble infini: propriétés, exemples

pour₁x + b₁ y = c₁

pour₂x + b₂ y = c₂

Comment trouver l'intersection entre une ligne et une courbe

Connaissant les équations de la ligne et de la courbe, le système d'équations est proposé et, dont les solutions correspondent aux points d'intersection. Si le système n'a pas de solution, la ligne n'est pas sécante à la courbe, et ce n'est pas non plus s'il y a un seul point de coupe, car, dans ce cas, la ligne est tangente à la courbe.

Pour que la ligne sèche, comme indiqué au début, le système d'équations doit avoir deux solutions ou plus.

Exemples de lignes de séchage

L'avion cartésien

Le plan cartésien est déterminé par deux lignes, appelées Axe x et Axe y, horizontal et vertical, respectivement. Ces lignes sont perpendiculaires et leur point d'intersection est appelé Origine du système de coordonnées, ou simplement origine.

La diagonale d'un polygone

Un polygone est une figure plate de trois côtés ou plus, qui rejoignent des points appelés sommets. Un segment qui rejoint deux sommets non consécutifs est une diagonale du polygone, et la ligne contenant ledit segment est sécable du polygone en question.

Une corde de circonférence

La corde d'une circonférence est le segment qui rejoint deux de ses points. La corde principale est le diamètre, qui passe nécessairement au centre de la circonférence. Eh bien, la ligne qui contient toute corde, y compris le diamètre, est une ligne de séchage à la circonférence.

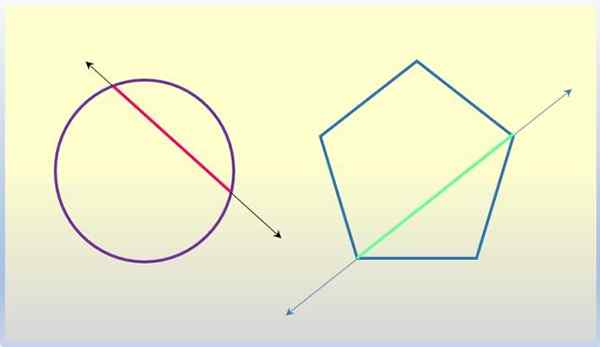Deuxième lignes aux chiffres géométriques. Source: F. Zapata.

La touche croisée

Avec cet outil, les noix qui maintiennent les pneus aux roues des véhicules sont desserrées. Les bras forment des lignes sèches et en même temps perpendiculaires.

Peut vous servir: variation proportionnelle

Alphabet

Certaines lettres d'alphabet se composent de traits droits qui déterminent sécant. Par exemple, la lettre X se compose de deux coups qui sont coupés ensemble en un point et la lettre T se compose de deux lignes perpendiculaires.

Exercices résolus

Exercice 1

Déterminez si les lignes données par:

L₁ : y = 5x - 3

L₂ : y = -2x + 1

Solution

La pente d'une ligne donnée sous la forme y = mx + b est la valeur de m, c'est-à-dire le coefficient qui accompagne le x. Depuis m₁ = 5 et m₂ = -2, qui sont différents, il est conclu que les lignes sont sèches.

Exercice 2

Quel est l'angle aigu entre les lignes d'exercice 1?

Solution

Les valeurs M sont directement remplacées₁ = 5 et m₂ = -2 dans la formule donnée dans les sections précédentes:

Par conséquent, l'angle entre les lignes est θ = arctg 0.777… = 37.9º.

Exercice 3

Quelle est l'intersection entre les lignes des exercices précédents?

Solution

Le système d'équations est proposé comme suit:

Dont la solution est: x = 4/7; y = -1/7 (peut être résolu par l'une des méthodes de résolution pour les systèmes d'équations, ou avec une calculatrice).

Par conséquent, le point d'intersection des lignes est: P (4/7; -1/7).

Les références

1. Géométrie analytique.Info. Deuxième ligne. Récupéré de: géométriaanalitique.Info.
2. Larson, R. 2006. Calcul avec géométrie analytique. 8e. Édition. McGraw Hill.
3. Lignes qui traversent. Récupéré de: Teacheraltuna.com.
4. Requena, b. Deuxième ligne. Récupéré de: universoformules.com.
5. Villena, m. Géométrie analytique dans R3. Récupéré de: dspace.Époustoufler.Édu.CE.