Caractéristiques, équations et exemples des droits oblicaux

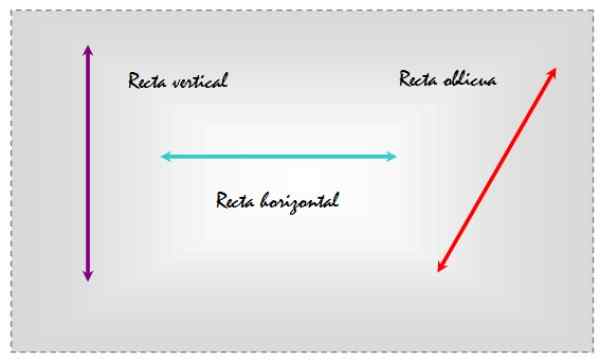
Le lignes obliques Ce sont ceux qui sont enclins, soit en ce qui concerne une surface plane ou une autre ligne qui indique une adresse particulière. Par exemple, considérez les trois lignes tracées dans un plan qui apparaît dans la figure suivante.

Nous connaissons leurs positions relatives respectives parce que nous les comparons à une ligne de référence, qui est généralement le Axe x qui désigne l'horizontal.

Figure 1. Lignes verticales, horizontales et obliques dans le même plan. Source: F. Zapata.

De cette façon, en choisissant la référence horizontale, la ligne gauche est verticale, le centre est horizontal et celui à droite est oblique, car il est incliné par rapport aux lignes de référence quotidiennes.

Maintenant, les lignes qui sont sur le même plan, comme la surface du papier ou de l'écran, occupent différentes positions les unes des autres, selon qu'elles se croisent ou non. Dans le premier cas, ils sont sèches droits, tandis que dans la seconde, ils sont parallèles.

D'un autre côté, les lignes de séchage peuvent également être des lignes droites obliques ou perpendiculaires. Dans les deux cas, les pentes des lignes sont différentes, mais les lignes obliques se forment entre elles des angles α et β, autres que 90º, tandis que les angles déterminés par les lignes perpendiculaires sont toujours à 90º.

Dans la figure suivante, ces définitions sont résumées:

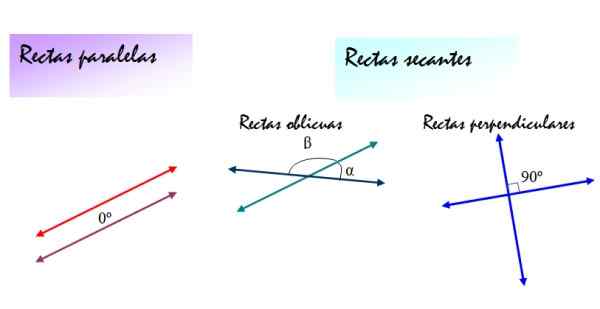Figure 2. Positions relatives entre les lignes: parallèles, obliques et perpendiculaires diffèrent à l'angle qui se forment entre eux. Source: F. Zapata.

[TOC]

Équations

Pour connaître les positions relatives des lignes dans le plan, il est nécessaire de connaître l'angle qu'ils se forment les uns avec les autres. Notez que les lignes sont:

Peut vous servir: calcul des approches à l'aide de différentiels

Parallèle: S'ils ont la même pente (direction égale) et ne se croisent jamais, leurs points sont donc équidistants.

Coïncide: Quand tous leurs points coïncident et ont donc la même pente, mais la distance entre leurs points est nul.

Sévères: Si vos boucles d'oreilles sont différentes, la distance entre leurs points varie et l'intersection est un seul point.

Ainsi, une façon de savoir si deux lignes dans le plan sont sèches ou parallèles est par sa pente. Les critères de parallélisme et de perpendicularité des lignes sont les suivants:

Être deux lignes L₁ et moi₂ appartenant à un avion, dont l'attente est respectivement m₁ et M₂. Ces lignes sont parallèles si m₁ = m₂ et ils sont perpendiculaires quand m₁= -1 / m₂

Si la connaissance des pentes de deux lignes dans le plan, aucun des critères ci-dessus n'est rempli, nous concluons que les lignes sont obliques. Connaissant deux points d'une ligne, la pente est calculée immédiatement, comme nous le verrons dans la section suivante.

Vous pouvez savoir si deux lignes sont sèches ou parallèles à trouver leur intersection, en résolvant le système d'équations qui se forment: s'il y a une solution, ils sont secs, s'il n'y a pas, ils sont parallèles, mais si les solutions sont infinies, les lignes sont coïncidence.

Cependant, ce critère ne nous informe pas sur l'angle entre ces lignes, même si elles ont l'intersection.

Pour connaître l'angle entre les lignes, deux vecteurs sont nécessaires ou et V qui appartiennent à chacun d'eux. Ainsi, il est possible de connaître l'angle qu'ils forment à travers le produit scalaire des vecteurs, défini de cette manière:

ou•v =ou.V.cos α

Équation de ligne dans le plan

Une ligne dans le plan cartésien peut être représentée de plusieurs manières, comme:

Il peut vous servir: équation générale de parabole (exemples et exercices)

-Formulaire en attente de l'interne: Ouais m C'est la pente de la ligne et b C'est l'intersection de la ligne avec l'axe vertical, l'équation de la ligne est y = mx + b.

-Équation générale pour une ligne droite: Ax + par + c = 0, où M = a / b C'est la pente.

Dans le plan cartésien, les lignes verticales et horizontales sont des cas particuliers de l'équation de la ligne.

-Lignes verticales: x = a

-Lignes horizontales: y = k

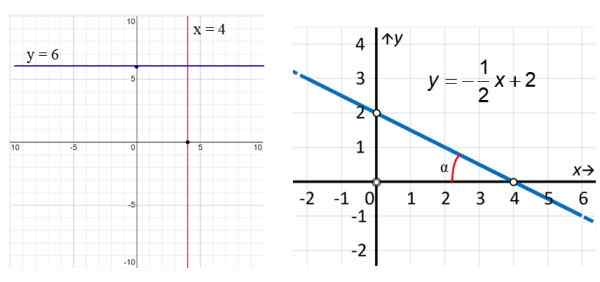figure 3. À gauche, la ligne verticale x = 4 et la ligne horizontale y = 6. À droite un exemple de ligne oblique. Source: F. Zapata.

Dans les exemples de la figure 3, la ligne rouge verticale a l'équation x = 4, tandis que la ligne parallèle à l'axe x (bleu) a l'équation y = 6. Quant à la bonne ligne, nous voyons qu'il est oblique et pour trouver son équation, nous utilisons les points mis en évidence sur la figure: (0,2) et (4.0) de cette manière:

M = (et₂ - et₁) / (X₂ - X₁) = (2 - 0) / (0 - 4) = - ½

La coupe de cette ligne avec l'axe vertical est y = 2, comme indiqué à partir des graphiques. Avec ces informations:

y = (-½) x + 2

La détermination de l'angle d'inclinaison par rapport à l'axe x est simple. Je sens ça:

α = arctg (2/4) = 26.6e

Par conséquent, l'angle positif de l'axe x à la ligne est: 180º - 26.6e = 153.4e

Exemples de lignes obliques

Figure 4. Exemples de lignes obliques. Source: Ian Patterson Wrathful [CC par (https: // CreativeCommons.Org / licences / par / 2.0)]. Tour penchée de Pise. Pixabay.

Les lignes obliques apparaissent dans de nombreux endroits, il s'agit de prêter attention à les trouver dans l'architecture, le sport, le câblage d'alimentation en électricité, les tuyaux et dans de nombreux autres endroits. Dans la nature, des lignes obliques sont également présentes, comme nous le verrons ci-dessous:

Peut vous servir: règles de dérivation (avec des exemples)

Les rayons de lumière

La lumière du soleil se propage en ligne droite, mais la forme arrondie de la terre affecte la façon dont la lumière du soleil affecte la surface.

Dans l'image ci-dessous, nous pouvons clairement apprécier que les rayons solaires affectent perpendiculairement les régions tropicales, mais à la place, ils arrivent obliquement à la surface dans les régions tempérées et dans les pôles.

Par conséquent, les rayons du soleil parcourent une distance plus longue à travers l'atmosphère et la chaleur se propage également sur une plus grande surface (voir figure). Le résultat est que les zones proches des pôles sont plus froides.

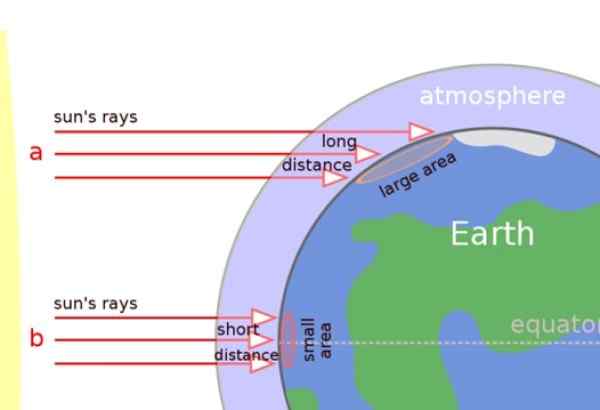Figure 5. Les rayons du soleil affectent obliquement les zones tempérées et les pôles, mais ils sont plus ou moins perpendiculaires sous les tropiques. Source: Wikimedia Commons.

Lignes qui ne sont pas dans le même plan

Lorsque deux lignes ne sont pas dans le même plan, elles peuvent toujours être obliques ou loué, Comme ils sont également connus. Dans ce cas, ses réalisateurs ne sont pas parallèles, mais n'appartenaient pas au même plan, ces lignes n'ont pas d'intersection.

Par exemple, les lignes de la bonne figure sont clairement dans différents plans. S'ils regardent d'en haut, il est observé qu'ils traversent efficacement, mais ils n'ont pas de point commun. Sur la droite, nous voyons les roues à vélo, dont les rayons semblent se croiser quand ils regardent droit devant.

Figure 6. Lignes obliques appartenant à différents avions. Source: gauche f. Zapata, pixabay droit.

Les références

1. Géométrie. Directeur vectoriel d'une ligne. Récupéré de: Juanbragado.est.
2. Larson, R. 2006. Calcul avec géométrie analytique. 8e. Édition. McGraw Hill.
3. Les mathématiques sont un jeu. Lignes et angles. Récupéré de: JuntadeandAlucia.est.
4. Lignes qui traversent. Récupéré de: Teacheraltuna.com.
5. Villena, m. Géométrie analytique dans R3. Récupéré de: dspace.Époustoufler.Édu.CE.