Zone d'un pentagone régulier et irrégulier comment il est pris, exerce

Pour calculer le zone d'un pentagone Nous devons d'abord déterminer si cela est régulier ou non. Un pentagone est un polygone, une figure plate fermée de cinq côtés. Lorsqu'un polygone est régulier, cela signifie que la longueur de ses côtés est la même et ses angles internes aussi.

Dans ce cas, il existe une formule pour calculer la zone exacte du polygone ordinaire, connaissant certaines de ses principales caractéristiques, que nous déduire plus tard.

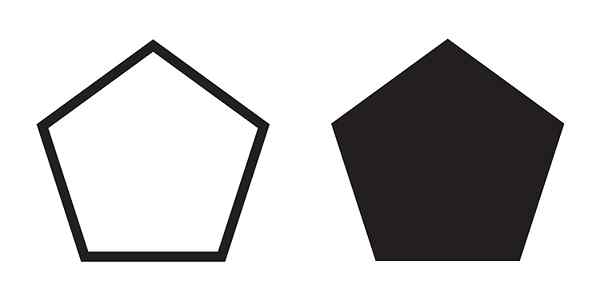Deux pentagones

Si le polygone n'est pas régulier, c'est-à-dire qu'il a des côtés de différentes tailles et des angles internes inégaux, il n'y a pas de formule unique.

Cependant, les mathématiciens ont trouvé des stratégies de calcul, telles que la division de la figure en autres avec le plus grand nombre de côtés, tels que les triangles, les carrés et les rectangles, dont les dimensions sont connues ou facilement calculées.

Une autre procédure pour calculer les zones de polygones en général, connaissant les coordonnées de ses sommets, est la méthode appelée DÉTERMINANTS DE GAUSS, que nous décrirons plus tard.

[TOC]

Comment calculer la zone d'un Pentagone ordinaire?

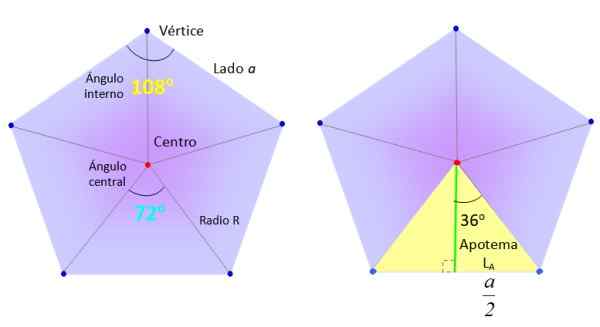
Nous allons prendre un Pentagone ordinaire du côté A, et nous le diviserons en 5 triangles égaux comme indiqué sur la figure, en dessinant des segments du centre (rouge) aux sommets (bleu).

Les éléments nécessaires pour trouver la zone du Pentagone ordinaire. Source: F. Zapata.

À son tour, les triangles, comme le jaune exceptionnel à droite dans la figure supérieure, sont divisés en deux rectangles égaux, grâce au segment vert, appelé apothème.

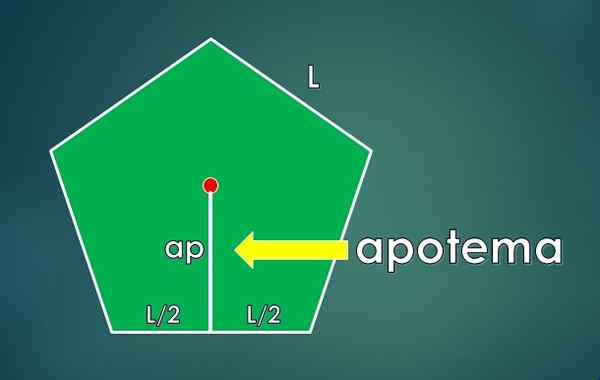
Apotheme est défini comme le segment perpendiculaire qui se connecte au centre du polygone au centre d'un côté. Sa longueur est L_POUR.

La zone d'un triangle rectangle de base a / 2 et hauteur L_POUR est:

[(A / 2) x l_POUR]]

Le Pentagone a 10 triangles comme celui-ci, donc sa zone est:

Peut vous servir: fonctions vectorielles

A = 10 (a / 2) x L_POUR

Mais le périmètre P du Pentagone est précisément p =10A, Par conséquent, la zone est donnée par le semi-produit du périmètre et la longueur de l'apothème:

A = p x l_POUR / 2

Zone du Pentagone ordinaire connaissant le côté un

Exprimant la longueur de l'apothem L_POUR Selon le côté A, sachant que l'angle indiqué est la moitié de l'angle central, soit 36 ​​°, équivalent à:

36º = π / 5

Par trigonométrie élémentaire, par tangente de l'angle aigu 36º:

Tan (π / 5) = (a / 2) ÷ l_POUR

Ainsi:

L_POUR=  (A / 2) ÷ tan (π / 5)

Remplacement dans la zone déduite dans la section précédente, et sachant que p = 5a:

A = p x l_POUR / 2

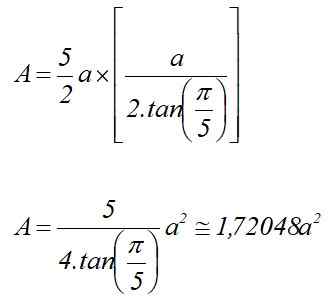
Zone du Pentagone ordinaire connaissant sa radio

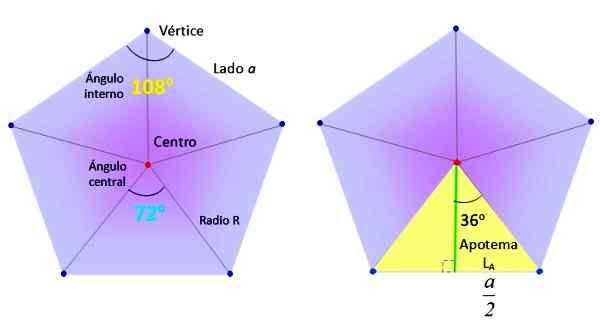
Il radio d'un polygone ordinaire est le segment qui va du centre à l'un de ses sommets. Il coïncide avec le rayon de la circonférence circonscrite, comme le montre la figure suivante:

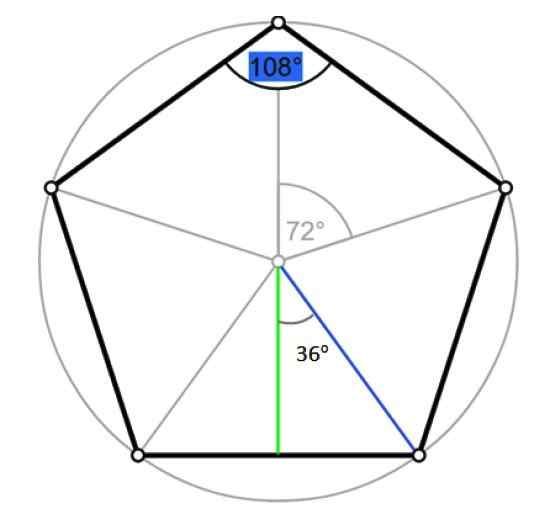Angles et apothème du Pentagone. Source: Wikimedia Commons / F. Zapata.

Soit R la mesure de ladite radio, qui coïncide avec l'hypoténuse du triangle droit délimité dans la figure précédente, en bleu. Par trigonométrie:

cos 36º = cos (π / 5) = l_POUR ÷ r

ET

sin 36º = sin (π / 5) = (a / 2) ÷ r

Donc:

A = p x l_POUR / 2 = 5r. péché (π / 5) x r. cos (π / 5) = 5r² [sin (π / 5) x cos (π / 5)]]

Utilisation de la formule à double angle:

sin (2θ) = 2 sen θ . cos θ

Nous devons:

[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º

Et donc, en remplacement de cette valeur, nous obtenons la formule suivante pour la zone du Pentagone ordinaire:

A = (5/2) R².Sen 72º

Comment calculer la zone d'un pentagone irrégulier?

Comme nous l'avons déjà dit, pour un polygone irrégulier, il n'y a pas de formule unique, mais il existe deux méthodes qui fonctionnent généralement très bien, la première est appelée triangulation et la seconde est la méthode des déterminants de Gauss.

Peut vous servir: Théorème d'existence et d'unicité: démonstration, exemples et exercices

Triangulation

Il consiste à diviser la figure en triangles, dont la zone est plus facile à calculer, ou peut également être testée avec d'autres figures dont la zone est connue, comme les carrés, les rectangles et les trapézides.

DÉTERMINANTS DE GAUSS

Une autre façon de trouver la zone du Pentagone irrégulière ou un autre polygone irrégulier est de placer la figure dans un système de coordonnées cartésiennes, afin de trouver les coordonnées des sommets.

Connues ces coordonnées, la méthode des déterminants Gauss est appliquée pour calculer la zone, qui est donnée par la formule suivante:

Où a est la zone du polygone et (x_n , et_n ) sont les coordonnées des sommets. Un polygone de n côtés a 5 sommets, pour le Pentagone, ce serait n = 5:

Les barres qui accompagnent la formule sont des barres de module ou une valeur absolue.

Cela signifie que bien que le résultat de l'opération soit négatif, nous devons l'exprimer avec un signe positif, et s'il est déjà positif, il doit être laissé avec ce signe. C'est parce qu'une zone est toujours un montant positif.

La procédure est appelée Gauss Determinants par son créateur, le mathématicien allemand Carl F. Gauss (1777-1855). Les opérations indiquées sont équivalentes au déterminant d'une matrice 2 × 2, par exemple le premier déterminant est:

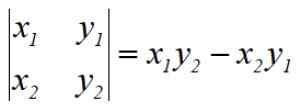
Pour trouver la zone du Pentagone, nous devons résoudre 5 déterminants, ajoutez le résultat algébriquement, divisez-le par 2 et exprimez enfin la zone toujours avec un signe positif.

Exercices résolus

Exercice 1

Trouvez la zone du Pentagone ordinaire dont l'apothème vaut 4 cm et dont l'équipe mesure 5.9 cm.

Solution

Puisqu'il s'agit d'un Pentagone ordinaire, et que nous avons la mesure du côté et de l'apothème, nous utilisons la formule déduite précédemment:

Peut vous servir: triangle scaleno

A = p x l_POUR / 2

Le périmètre p est égal à 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Exercice 2

Trouvez la zone du pentagone irrégulier montré. Les dimensions suivantes sont connues:

Dc ≈ de

Ae = ab = 5

BC = 12

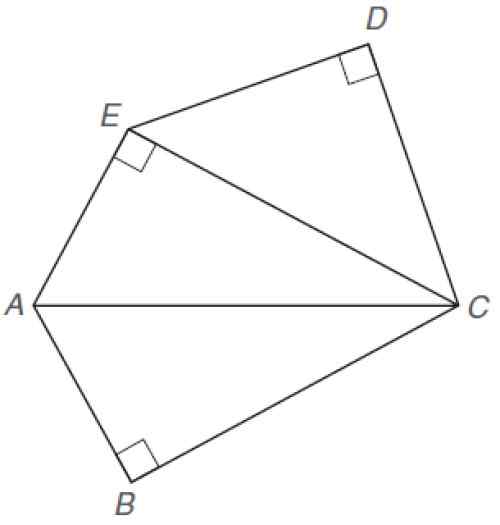Pentagone irrégulier. Source: Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.

Solution

La zone du Pentagone est la somme des zones des triangles, qui sont des rectangles. La déclaration indique que DC ≈ de, donc lors de l'application du théorème de Pythagore au triangle EDC, il a:

CE² = 2 ed². Alors ec = √2.Élégant.

Les triangles AEC et ABC ont une hypoténuse commune, qui est donc le segment AC:

EA² + CE² = Ab² + avant JC²

Comme EA et AB mesurent les mêmes, il est obtenu que:

Ec = bc = √2.Élégant

Depuis BC = 12, alors Ed = 12 / √2 = 8.485.

Avec ces valeurs, nous calculerons la zone de chaque triangle et les ajouterons à la fin.

Zone de triangle EDC 

Ed x DC / 2 = 8.485² / 2 = 36

Zone de triangle AEC 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

ABC Triangle Area 

AB x BC / 2

Ensuite, la zone recherchée est:

5 x 12/2 = 30

C'est la même chose que celle de Triangle AEC, car les deux ont les mêmes mesures.

Pentagone irrégulier

Enfin, la zone demandée est la somme des zones des trois triangles:

A = 36 + 30 + 30 unités = 96 unités.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Référence ouverte en mathématiques. Zone de polygone. Récupéré de: MathpenRef.com.
3. Formules d'univers. Zone d'un pentagone irrégulier. Récupéré de: universoformules.com.
4. Formules d'univers. Zone d'un pentagone ordinaire. Récupéré de: universoformules.com.
5. Wikipédia. Pentagone. Récupéré de: est.Wikipédia.com.